Collier (combinatoire)
En combinatoire, un collier de k perles de longueur n est un mot circulaire ou encore une classe d'équivalence de suites de n symboles sur un alphabet de taille k, en considérant comme équivalents tous les décalages circulaires de la suite. Un collier peut être vu comme étant formé de n perles de k couleurs enfilés en cercle.
Un bracelet, aussi appelé collier libre ou collier reversible est une classe d'équivalence de suites de symboles sous les deux opération de décalage circulaire et de réflexion ou retournement.
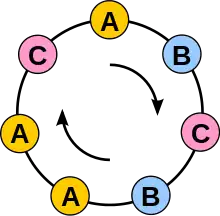
Dans l'exemple ci-contre, le bracelet est la classe d'équivalence du mot ABCBAAC ; selon que l'on lit dans sens direct ou le sens inverse, il y a deux colliers, qui sont les classes des mots ABCBAAC et CAABCBA.
En termes techniques, un collier est une orbite de l'action du groupe cyclique d'ordre n, alors qu'un bracelet est une orbite de l'action du groupe diédral.
Dénombrements de colliers
Nombre de colliers
Il y a
colliers de longueur sur un alphabet de taille . Ici, est l'indicatrice d'Euler[1]. Pour , c'est la suite A000031 de l'OEIS et pour tout la suite A054631 de l'OEIS. Pour n=3 et n=4 les colliers sont 000,001,011,111 et 0000,0001,0011,0101,0111,1111. Il y a aussi
colliers de longueur sur un alphabet de taille ou chaque lettre est présente au moins une fois. représente les Nombres de Stirling de seconde espèce. est la suite A087854 de l'OEIS et est reliée à au travers des coefficients binomiaux:
et
Nombre de bracelets
Il y a
bracelets de longueur sur un alphabet de taille , où est le nombre de colliers de longueur sur un alphabet de taille .
Exemples
Exemples de colliers
Si les perles d'un collier de longueur sont toutes distinctes, alors le nombre de colliers est , le nombre de permutations circulaires d'ordre .
Si, au contraire, toutes les perles sont identiques, il n'y a qu'un seul collier de cette couleur, donc au total autant de collier que de symboles dans l'alphabet.
Exemples de bracelets
Si les perles d'un collier de longueur sont toutes distinctes, le nombre de bracelets est pour . Ce n'est pas , puisque dans ce nombre on compte aussi des bracelets dont les perles ne sont pas toutes distincts.
Colliers apériodiques

Un collier apériodique est la classe d'équivalence de suites dont deux rotations non triviales ne sont jamais égales. Il est équivalent de dire qu'un collier apériodique est la classe d'un mot primitif, c'est-à-dire d'un mot qui n'est pas puissance d'un autre mot. L'exemple du début, qui correspond au mot ABCBAAC, est une collier primitif.
Le nombre de colliers apériodiques de longueur n sur un alphabet à k lettres est
- .
Ici, est la fonction de Möbius. Les fonctions sont aussi appelés les polynômes de colliers (en la variable ), et la formule ci-dessus est attribuée au colonel Moreau. En fait, Moreau ne compte pas les colliers apériodiques, mais les colliers tout court, et même les colliers contenant une certaine répartition du nombre de perles de chaque couleur, ce qui rend sa formule moins limpide.
Pour , la suite des est la suite A001037 de l'OEIS. Pour et , les colliers apériodiques binaires sont 001,011 et 0001,0011,0111.
La formule ci-dessus est dérivée de l'expression
et s'obtient par inversion de Möbius.
Pour établir la formule, on répartit les mots de longueur : chaque mot appartient à un et un seul collier. Si ce collier n'est pas apériodique, le mot n'est pas un mot primitif, et il est puissance d'un mot primitif unique dont la longueur divise . Ce mot primitif appartient à un collier de longueur . Ainsi, chaque mot de longueur est dans un collier apériodique de longueur divisant , et chaque collier contient exactement d mots. Ceci prouve la formule.
Les colliers apériodiques apparaissent dans les contextes suivants :
- Le nombre de mots de Lyndon de longueur sur lettres : Tout collier apériodique correspond à un unique mot de Lyndon, de sorte que les mots de Lyndon forment un système de représentants de colliers apériodiques.
- est la dimension de la composante homogène de degré de l'algèbre de Lie libre sur générateurs. C'est la formule de Witt[2]
- est le nombre de polynômes unitaires irréductibles de degré sur un corps fini à éléments lorsque une puissance d'un nombre premier.
- C'est aussi l'exposant dans l'identité cyclotomique (en) :
Premières valeurs
Voici les expressions des polynômes de colliers pour de petites valeurs de n :
- Quand est un nombre premier, on a .
Enfin,
- ,
Formule du produit de colliers
Le produit des nombres de colliers de longueur , sur symboles, admet une limite quand croît et est fixe ; c'est
- .
Le coefficient de dans le développement du produit (au facteur près) est le nombre de permutations de avec inversions, aussi appelé un nombre de MacMahon. C'est la suite A008302 de l'OEIS (Contribution de Mikhail Gaichenkov).
Articles connexes
- Mot de Lyndon
- Problème du partage d'un collier
- Permutation
- Preuve du petit théorème de Fermat par double dénombrement
- nombre de Forte (en) utilisé en musique atonale. Les nombres de Forte correspondent aux bracelets binaires de longueur 12.
- Necklace ring (en)
Notes et références
Notes
- (en) Eric W. Weisstein, « Necklace », sur MathWorld
- Lothaire 1997, p. 79,84
Références
- M. Lothaire, Combinatorics on words, Cambridge University Press, coll. « Cambridge Mathematical Library », , xviii+238 (ISBN 978-0-521-59924-5, DOI 10.1017/CBO9780511566097, MR 1475463, présentation en ligne)Seconde édition, légèrement révisée, du livre paru sous le même nom, en 1983, chez Addison-Wesley, dans la série « Encyclopedia of Mathematics and its Application », (ISBN 978-0-201-13516-9)
- (en) Richard P. Stanley, Enumerative Combinatorics [détail des éditions] (présentation en ligne)
- C. Moreau, « Sur les permutations circulaires distinctes », Nouvelles annales de mathématiques, journal des candidats aux écoles polytechnique et normale, 2e série, vol. 11, , p. 309–314 (lire en ligne)
- Nicholas Metropolis et Gian-Carlo Rota, « Witt vectors and the algebra of necklaces », Advances in Mathematics, vol. 50, no 2, , p. 95–125 (DOI 10.1016/0001-8708(83)90035-X, MR 723197, zbMATH 0545.05009)
- Gabriele Fici, Antonio Restivo et Laura Rizzo, « Minimal forbidden factors of circular words », Theoretical Computer Science, vol. 792, , p. 144–153 (DOI 10.1016/j.tcs.2018.05.037)
Lien externe
(en) Frank Ruskey, « Information on Necklaces, Lyndon Words, de Bruijn Sequences ».


































![\displaystyle M_{kr}(n)=\sum_{[i,j]=n}(i,j)M_k(i)M_r(j)](https://img.franco.wiki/i/074b037e627cca0b99a05bb29daa0a5be9831000.svg)

![[i,j]](https://img.franco.wiki/i/fff46b0cabba9dd4a48696b0d6f85eb38192a021.svg)




