Nombre de Catalan
En mathématiques, et plus particulièrement en combinatoire, les nombres de Catalan forment une suite d'entiers naturels utilisée dans divers problèmes de dénombrement, impliquant souvent des objets définis de façon récursive. Ils sont nommés ainsi en l'honneur du mathématicien belge Eugène Charles Catalan (1814-1894) qui les a étudiés en 1838, mais étaient déjà connus d'Euler.
Le nombre de Catalan d'indice n est défini par :
Pour , on peut écrire :
(voir Coefficient binomial central).
Les dix premiers nombres de Catalan (pour n de 0 à 9) sont :
Historique
La suite de Catalan est décrite pour la première fois en 1751 par le Suisse Leonhard Euler : dans une lettre à Goldbach, il pose le problème du dénombrement des triangulations d'un polygone, trouve les 8 premiers nombres, suggère une formule de produit explicite et trouve une forme explicite pour la fonction génératrice[1] - [2] . Ce problème de triangulation est d'ailleurs aussi à l'origine indirecte du sudoku américano-japonais[3].
En 1758, Johann Andreas Segner reprend le problème des triangulations (faisant explicitement référence à Euler), prouve une relation de récurrence quadratique et utilise la formule pour calculer les 18 premiers nombres, les 6 derniers de manière incorrecte [4] - [2]. Les futurs nombres de Catalan prennent alors le nom de nombres de Segner.
Ce n'est qu'en 1838 qu'Eugène Charles Catalan pose et résout le problème du "nombre de manières d'effectuer le produit de n facteurs différents" [5].
En 1839 Catalan fait le lien avec le nombre de triangulations[6], et publie un article complet sur le sujet en 1887[7]. Depuis, le nom de Catalan remplace celui de Segner.
L'astuce de comptage des mots de Dyck est trouvée par Désiré André en 1887.
En 1988, dans la revue chinoise Neimenggu Daxue Xuebao, a été publié le fait que la suite des nombres de Catalan avait été utilisée en Chine par le mathématicien Ming Antu (ou Minggatu) dès 1730, lors de l'écriture de son livre Ge Yuan Mi Lu Jie Fa (en), achevé par son élève Chen Jixin en 1774 et publié 60 ans plus tard.
P. J. Larcombe esquissa en 1999 certaines des caractéristiques du travail de Ming Antu, comme le fait qu'il utilisa la suite des nombres de Catalan pour exprimer des développements en séries de sin(2α) et sin(4α) en termes de sin(α)[8].
Propriétés et comportement asymptotique
Une autre expression pour est
ce qui est équivalent à l'expression précédente car . Cela montre que est un entier naturel, ce qui n'est pas évident de prime abord à partir de la première formule.
Les nombres de Catalan satisfont aussi à la relation de récurrence
De plus,
Cela est dû au fait que . Ils vérifient aussi et , ce qui peut être un moyen plus efficace pour les calculer.
La formule de Stirling permet de calculer un équivalent asymptotique de la suite des nombres de Catalan[9] :
Un résultat dû à Ernst Kummer, et qui se déduit trivialement de la relation de récurrence indiquée plus haut, aboutit à ce que les seuls nombres de Catalan impairs sont ceux pour lesquels . Tous les autres sont pairs.
Applications en combinatoire
Il existe de nombreux problèmes combinatoires dont la solution est donnée par les nombres de Catalan. Les nombres de Catalan peuvent être interprétés de différentes façons dont voici quelques exemples :
- est égal au nombre de mots de Dyck de longueur 2n.
- est également le nombre de façons différentes de placer des parenthèses autour de n + 1 facteurs, pour préciser une expression faisant intervenir n fois une loi de composition interne non associative.
- est également le nombre d'arbres binaires entiers à n + 1 feuilles.
- est aussi égal au nombre de façons de découper en triangles un polygone convexe à n + 2 côtés en reliant certains de ses sommets par des segments de droite.
- est le nombre de chemins monotones le long des arêtes d'une grille à n × n carrés, qui restent sous (ou au niveau de) la diagonale.
- est le nombre de trajectoires de longueur 2n + 1 d'une marche aléatoire simple qui ont la propriété d'aller de la hauteur 0 à la hauteur 1 en restant négatif ou nul lors des 2n premières étapes.
- est le nombre d'arbres planaires enracinés à n arêtes.
Mots de Dyck
Un mot de Dyck est une chaîne de caractères formée de n lettres X et de n lettres Y, telle qu'aucun préfixe (mot obtenu en supprimant les dernières lettres à partir d'un rang quelconque) ne contienne strictement plus de Y que de X. Autrement dit, lorsque nous parcourons un mot de Dyck de gauche à droite, le nombre de X rencontrés est toujours supérieur ou égal au nombre de Y. Par exemple, les mots de Dyck de la longueur 6 sont:
En l'occurrence, C3= 5.
Assimilant X à une parenthèse ouvrante et Y à une parenthèse fermante, un mot de Dyck de longueur 2n peut être vu comme une expression formée de n paires de parenthèses correctement assemblées : ((())), ()(()), ()()(), (())(), (()()) ; voir aussi Langage de Dyck. Les mots de Dyck peuvent être naturellement représentés comme des chemins dans un quadrillage de n + 1 points par n + 1 points, reliant certains points par les traits verticaux et horizontaux. Ces chemins commencent dans le coin inférieur gauche, et se terminent dans le coin supérieur droit, en allant toujours vers le haut ou vers la droite, mais ne passant jamais au-dessus de la diagonale principale. X représente alors un « déplacement vers la droite » et Y représente un « déplacement vers le haut ».
Nous pouvons compter les mots de Dyck avec l'astuce suivante appelée principe de symétrie : intéressons-nous aux mots contenant n X et n Y qui ne sont pas des mots de Dyck. Dans de tels mots, déterminons le premier Y qui brise la condition de Dyck, puis modifions toutes les lettres qui suivent ce Y, en échangeant X avec Y et vice versa. Nous obtenons un mot avec n + 1 Y et n - 1 X, et en fait tous les mots comportant n + 1 Y et n - 1 X peuvent être obtenus par ce moyen et de manière unique. Le nombre de ces mots est le nombre de façons de placer les n - 1 X dans 2n emplacements et est égal à
ce qui donne le nombre de mots qui ne sont pas de Dyck ; le nombre de mots de Dyck est égal à
qui est le n-ième nombre de Catalan .
Notons que ce dénombrement est celui posé dans le problème du scrutin au sens large.
Une généralisation au cas où les lettres X et Y ne sont pas en même quantité se trouve dans l'article sur le triangle de Catalan.
Nombre de parenthésages dans un produit
est le nombre de façons différentes de placer des parenthèses autour de n + 1 termes, pour préciser une expression faisant intervenir n fois une loi de composition interne. Pour n = 3 par exemple, la loi étant notée multiplicativement, nous obtenons 5 façons différentes de placer des parenthèses autour de 4 facteurs : .
Lorsque la loi est associative, chaque parenthésage donne le même résultat, mais peut conduire à des temps de calcul différents. En particulier pour un produit matriciel le nombre de multiplications scalaires à effectuer change suivant les parenthésages, et dans la pratique, cela peut rendre nécessaire l'utilisation d'algorithmes de multiplication de matrices enchaînées.
Triangulations d'un polygone
est aussi égal au nombre de façons de découper en triangles un polygone convexe à côtés en reliant certains de ses sommets par des segments de droite.
Arbres binaires
est également le nombre d'arbres binaires à n nœuds (internes et externes).
est aussi le nombre d'arbres binaires entiers à n + 1 feuilles[n 1]. La correspondance entre les produits non associatifs, les triangulations d'un polygone et les arbres binaires entiers est illustré sur l'image ci-dessous.
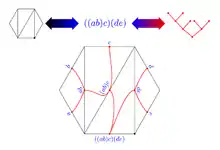
Partitions non croisées
est également le nombre de partitions non croisées de l'ensemble {1, … , n}. A fortiori, n'excède jamais le n-ième nombre de Bell, ce qui était asymptotiquement attendu, puisque les nombres de Bell croissent bien plus vite que , une autre borne des nombres de Catalan, découlant par exemple de leur définition comme nombre de mots de Dyck de longueur 2n.
Chemins sous-diagonaux dans le carré
est le nombre de chemins monotones le long des arêtes d'une grille à n × n carrés, qui restent sous (ou au niveau de) la diagonale. Un chemin monotone part du coin Sud-Ouest, arrive dans le coin Nord-Est, et est constitué d'arêtes dirigées à droite ou vers le haut. Un mot de Dyck encode un tel chemin de la manière suivante : X signifie « va à droite » et Y signifie « monte ». Les diagrammes ci-dessous représentent le cas n = 4 :
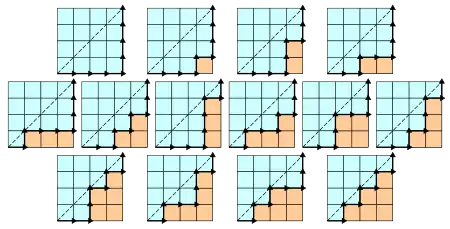
Pour , l'aire totale sous les chemins vaut : (suite A029760 de l'OEIS).
Trajectoires de la marche aléatoire simple
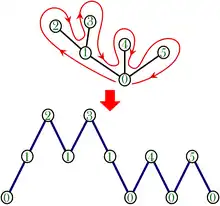
est le nombre de trajectoires de longueur 2n + 1 d'une marche aléatoire simple qui ont la propriété d'aller de la hauteur 0 à la hauteur 1 en restant négatif ou nul lors des 2n premières étapes. On peut voir cela en faisant pivoter de 45 degrés le chemin entre les deux coins d'un carré décrit lors du premier exemple. C'est aussi le nombre de trajectoires de longueur 2n + 2 allant de la hauteur 0 à la hauteur 0 en restant strictement positives lors des 2n + 1 étapes intermédiaires, ou encore le nombre de trajectoires de longueur 2n allant de la hauteur 0 à la hauteur 0 en restant positives ou nulles lors des 2n – 1 étapes intermédiaires. Dans ce dernier cas on peut coder la trajectoire par une suite de 2n signes + et – (pour montée et descente), la condition de positivité se traduisant par le fait que cette suite est un mot de Dyck (car chaque préfixe a plus de montées que de descentes). Ainsi, pour la marche aléatoire simple, la probabilité que le premier temps de retour en 0, partant de 0, ait lieu à l'instant 2n + 2, est , le facteur 2 prenant en compte les trajectoires strictement négatives en plus des trajectoires strictement positives. De même, la probabilité que le premier temps d'atteinte de 1, partant de 0, ait lieu à l'instant 2n + 1, est .
Arbres planaires
est le nombre d'arbres planaires enracinés à n arêtes. La bijection avec les mots de Dyck, ou encore avec les trajectoires de marches aléatoires, est donnée très visuellement par un parcours extérieur de l'arbre. La trajectoire obtenue est le graphe de la fonction qui à chaque coin (secteur angulaire délimité par un sommet et deux arêtes contigües issues de ce sommet) associe la hauteur du sommet (la distance du sommet à la racine). Les coins sont parcourus dans l'ordre correspondant au parcours autour de l'arbre (voir figure ci-contre). Chaque sommet est visité autant de fois qu'il y a de coins issus de ce sommet, c.-à-d. le nombre de visites à un sommet est le degré de ce sommet ; à titre d'exception, le nombre de visites à la racine est son degré plus un (plus le retour final à la racine, qui revient à visiter deux fois le coin origine). Ainsi le nombre de pas de la marche est la somme des degrés du graphe, c.-à-d. deux fois le nombre d'arêtes du graphe.
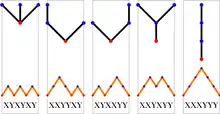
Bijections entre les exemples
Les ensembles décrits plus haut qui sont à éléments sont clairement en bijection les uns avec les autres.
Les bijections entre deux ensembles symétriques (produits non associatifs, triangulations d'un polygone, arbres binaires entiers) sont décrits plus haut. De même les bijections entre deux ensembles latéralisés (mots de Dyck, chemins monotones sous la diagonale, marches aléatoires positives, arbres planaires) sont décrits dans les sections précédentes. La bijection entre les arbres binaires entiers à 2n arêtes et les arbres planaires à n arêtes se fait en contractant soit les arêtes gauches, soit les arêtes droites de l'arbre binaire. D'où les appellations « symétriques » et « latéralisés ».
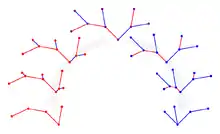
L'image suivant illustre les différentes bijections avec un exemple concret :

Relations de récurrence
- Comme vu précédemment, les nombres de Catalan satisfont la relation de récurrence
Ceci vient du fait que tout mot de Dyck w de longueur supérieure à 2 peut s'écrire de manière unique sous la formeoù w1 et w2 désignent des mots de Dyck (éventuellement vides). La série génératrice des nombres de Catalan est définie paret en utilisant la relation de récurrence ci-dessus, on voit queet par conséquent[n 2];réciproquement, partant de la série génératrice, on obtient aisément la formule explicite des en utilisant le développement de Newton de ; ce passage d'une relation de récurrence à une formule explicite est une des utilisations les plus importantes des séries génératrices.
- D'autre part, ils satisfont la relation de récurrence
qui permet aussi de retrouver la série génératrice, en effet, cette relation montre que est la solution de l'équation différentiellequi vaut 1 en 0.
- Ils satisfont enfin à la relation de récurrence de Jacques Touchard :
.
Matrice de Hankel
La matrice de Hankel d'ordre n dont le terme est le nombre de Catalan a pour déterminant 1, indépendamment de la valeur de n.
Ainsi, pour n = 4, nous avons
De plus, si les termes sont « décalés », en prenant les nombres de Catalan , le déterminant est toujours 1, indépendamment de la valeur de n[n 3].
Ainsi, pour n = 4, nous avons
La suite des nombres de Catalan est la seule suite de nombres[n 4] ayant cette double propriété.
Notes et références
Notes
- Un arbre binaire est dit entier (ou plein) si chaque nœud a soit 0 soit 2 fils. Un tel arbre à n + 1 feuilles a aussi n nœuds internes, et 2n arêtes.
- Cette écriture est parfaitement rigoureuse dans le cadre des séries formelles ; si on interprète comme une série entière, l'expression asymptotique de montre que le rayon de convergence de la série est 1/4, et que sur l'intervalle réel , on a , en prolongeant le membre de droite en 0 par la valeur 1.
- En revanche, ce n'est plus le cas pour un décalage de 2 lignes : .
- L'existence et l'unicité d'une telle suite se démontre aisément par récurrence, mais il est nettement moins aisé de vérifier qu'on obtient ainsi la suite des nombres de Catalan.
Références
- (de) Leonhard Euler, « Lettre CXL », sur eulerarchive.maa.org
- (en) Igor pak, « Catalan numbers page »
- "Ouest-France" du 18 août 2021 in fine.
- (la) Johann Andreas Segner, « Enumeratio modorum quibus figurae planae rectilinae per diagonales dividuntur in triangula », Novi Commentarii Academiae Scientiarum Imperialis Petropolitanae, vol. 7, 1758/59, publié en 1761 (lire en ligne)
- E. Catalan, « Note sur une équation aux différences finies », Journal de Mathématiques pures et appliquées, no 3, , p. 515-516 (lire en ligne)
- E. Catalan, « Solution nouvelle de cette question: un polygone étant donné, de combien de manières peut-on le partager en triangles au moyen de diagonales ? », Journal de mathématiques pures et appliquées x, 1re série, no 4, , p. 91-94. (lire en ligne)
- E. Catalan, « Sur les nombres de Segner », Rend. Circ. Mat. Palermo 1 (1887), 190–201., no 1, , p. 190-201 (lire en ligne)
- (en) Luo Jianjin, « Ming'antu and His Power Series Expansions », Institute for the History of Science, Inner Mongolia Normal University; Institute of Science, Technology and Culture, Zhejiang University.
- On trouvera une analyse plus précise de ce développement asymptotique dans Analytic Combinatorics, p. 383.
Voir aussi
Bibliographie
- (en) Richard P. Stanley, Enumerative Combinatorics, vol. 1 et 2 [détail des éditions] (présentation en ligne)
- (en) Philippe Flajolet et Robert Sedgewick, Analytic Combinatorics, Cambridge University Press, (ISBN 0-521-89806-4, lire en ligne)
- Aubrey Blecher, Charlotte Brennan et Arnold Knopfmacher, « Water capacity of Dyck paths », Advances in Applied Mathematics, vol. 112, , article no 101945 (ISSN 0196-8858, DOI 10.1016/j.aam.2019.101945)
Articles connexes
- Triangle de Catalan
- Coefficient binomial central
- Algorithme de Rémy
- Nombre de Delannoy
- Nombre de Fuss-Catalan (en)
Liens externes
- (en) Eric W. Weisstein, « Catalan Number », sur MathWorld
- [vidéo] El ji, Deux (deux ?) minutes pour... les nombres de Catalan sur YouTube, (consulté le )
- Texte de la vidéo précédente.







































![{\displaystyle [-1/4,1/4]}](https://img.franco.wiki/i/3c399ffca8b7b0712872828c41ea5b8fb7064bfd.svg)


