Algorithme de Rémy

L'algorithme de Rémy est dû à Jean-Luc Rémy, chercheur au Centre de recherche en informatique de Nancy. Il a été créé en 1978 sans être publié immédiatement[1] et a fait partie du folklore de l'algorithmique et de la combinatoire énumérative[2] jusqu'à sa parution dans une revue francophone en 1985[3].

Les arbres binaires sont dénombrés par les nombres de Catalan ${\displaystyle C_{n}}$ donnés par les formules de récurrence :

${\displaystyle C_{0}=1}$

${\displaystyle C_{n+1}=\sum _{i=0}^{n}C_{i}C_{n-i}}$.

Mais ces formules ne permettent pas de dériver un algorithme efficace de génération aléatoire.

L'idée de Rémy consiste à non plus compter les arbres binaires à ${\displaystyle n}$ nœuds, mais les arbres binaires décorés à ${\displaystyle n}$ nœuds, à savoir les arbres dont les feuilles ont été décorées par les nombres de ${\displaystyle 0}$ à ${\displaystyle n}$ dans un ordonnancement quelconque. Il y a ${\displaystyle (n+1)!}$ manières de décorer un arbre binaire, par conséquent, le nombre d'arbres binaires à ${\displaystyle n}$ nœuds internes est

${\displaystyle D_{n}=(n+1)!C_{n}={\frac {(2n)!}{n!}}=2(2n-1)D_{n-1}.}$

Comme le note Knuth, Olinde Rodrigues avait déjà démontré cette formule, en 1838, dans un article du Journal de Liouville[4]. On note au passage que cela correspond à la récurrence linéaire sur les nombres de Catalan :

${\displaystyle C_{n}={\frac {2(2n-1)}{n+1}}C_{n-1}}$.

Rémy a remarqué qu'il y a ${\displaystyle 2(2n-1)}$ moyens de construire un arbre décoré de taille ${\displaystyle n}$ à partir d'un arbre décoré de taille ${\displaystyle n-1}$. On choisit un nœud interne ou externe (une feuille) dans cet arbre, appelons le ${\displaystyle x}$. Comme il y a ${\displaystyle n-1}$ nœuds internes et ${\displaystyle n}$ feuilles, il y a ${\displaystyle 2n-1}$ choix possibles de ${\displaystyle x}$. On insère alors un nouveau nœud interne ${\displaystyle \bullet }$ et une nouvelle feuille décorée par ${\displaystyle n}$, dont elle est la fille droite ou la fille gauche, tandis que ${\displaystyle x}$ en est alors le fils gauche ou le fils droit, comme cela est illustré dans les dessins ci-dessous.

• 
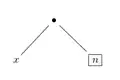  ${\displaystyle x}$ à gauche
• 
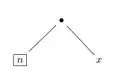  ${\displaystyle x}$ à droite

La suite d'arbres ci-dessus illustre des insertions de nœuds conduisant à la construction d'un arbre binaire de taille ${\displaystyle 6}$.

Une suite d'arbres décorés illustrant l'algorithme de Rémy

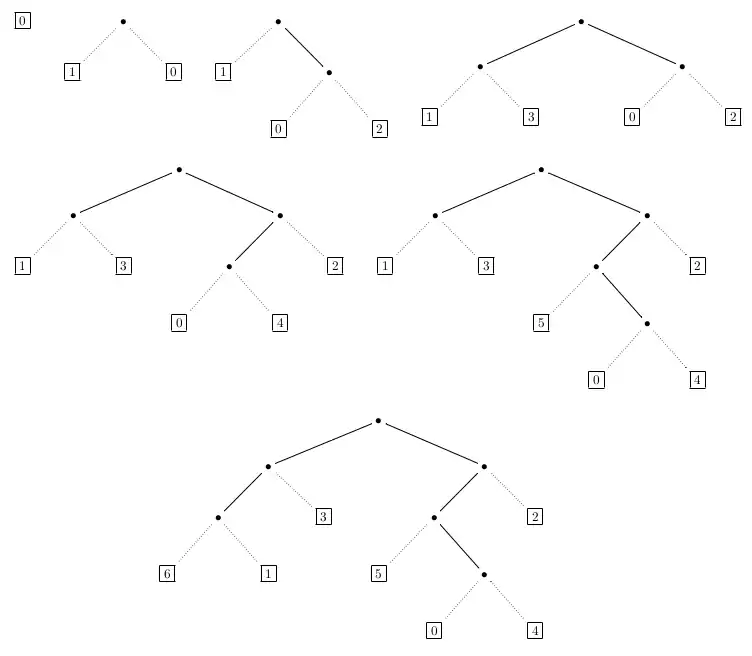
On voit que ce processus est unique ; en effet, l'insertion peut être inversée par la coupe de la feuille de plus grand numéro. En conséquence, la construction de Rémy produit aléatoirement des arbres décorés de façon uniforme. Il suffit d'oublier les feuilles pour obtenir une génération aléatoire des arbres ordinaires (donc non décorés).

Pour engendrer aléatoirement un arbre de taille ${\displaystyle n}$, on peut écrire un algorithme efficace qui utilise un tableau de taille ${\displaystyle 2n+1}$ et qui fait ${\displaystyle n-1}$ tirages aléatoires dans des intervalles d'entiers, de taille respectivement, ${\displaystyle 2}$ jusqu'à ${\displaystyle n}$, d'où une complexité linéaire de l'algorithme en nombre de tirage uniforme dans un intervalle discret. Il est possible d'améliorer cet algorithme et d'atteindre un algorithme optimal en nombre de bits aléatoires utilisés[5].

L'algorithme de Rémy est à l'origine de plusieurs échantillonneurs aléatoires efficaces d'arbres non binaires comptés par des nombres qui sont solutions d'équations holonomes (en)[5], notamment d'échantillonneurs aléatoires pour les arbres unaires-binaires.

• Jean-Luc Remy, « Un procédé itératif de dénombrement d'arbres binaires et son application à leur génération aléatoire », ITA, vol. 19(2),‎ 1985, p. 179-195 (lire en ligne)
• Donald E. Knuth, The Art of Computer Programming, vol. 4.4 (Generating all Trees), Addison Wesley, p. 18

• Arbre (mathématiques)
• Arbre (graphe)
• Nombre de Catalan
• Nombre de Motzkin
• Nombre de Schröder-Hipparque