Sudoku
Le sudoku (数独, prononcé /sɯː.do.kɯ/ en japonais, /su.do.ku/ ou /sy.do.ky/ en français), est un jeu en forme de grille défini en 1979 par l’Américain Howard Garns, mais inspiré du carré latin, ainsi que du problème des 36 officiers du mathématicien suisse Leonhard Euler.

Le but du jeu est de remplir la grille avec une série de chiffres (ou de lettres ou de symboles) tous différents, qui ne se trouvent jamais plus d’une fois sur une même ligne, dans une même colonne ou dans une même région (également appelée « bloc », « groupe », « secteur » ou « sous-grille »). La plupart du temps, les symboles sont des chiffres allant de 1 à 9, les régions étant alors des carrés de 3 × 3. Quelques symboles sont déjà disposés dans la grille, ce qui autorise une résolution progressive du problème complet.

Étymologie
Le nom sudoku (数独) est né de l’abréviation de la règle japonaise du jeu « Sūji wa dokushin ni kagiru » (数字は独身に限る), signifiant littéralement « chiffre (数字) limité (限る) à un seul (独身) » (sous-entendu par case, par ligne et par colonne). Cette abréviation associe les caractères sū (数, « chiffre ») et doku (独, « unique »). Ce nom est une marque déposée au Japon de l’éditeur Nikoli Corporation Ltd. En japonais, ce mot est prononcé [sɯː.do.kɯ] ; en français, il est couramment employé avec une prononciation francisée, c’est-à-dire en ignorant la voyelle longue présente sur le premier « u » et en modifiant légèrement le timbre des voyelles « u » : [sy.do.ky]. Au Japon, Nikoli est toujours propriétaire du nom sudoku[1] ; ses concurrents utilisent donc un autre nom : ils peuvent renvoyer au jeu par le nom américain original « Number Place[2] » (anglais : place numérale), ou encore par le mot « Nanpure » (ナンプレ), plus court. Quelques éditeurs non japonais orthographient le titre « Su Doku ».
Histoire
Probablement inspiré par le carré magique, ce jeu est tout d'abord connu des mathématiciens chinois, à partir de -650, sous le nom Luoshu (洛书, , « Livre de la rivière Luo »). D'ordre 3, il pouvait alors être représenté par différents symboles et utilisé dans le feng shui.
Ce sont visiblement les Indiens, inventeurs des signes dits chiffres arabes, qui les limitèrent à des chiffres[3], puis les Arabes, probablement vers le VIIe siècle, lorsque leurs armées firent la conquête du Nord-Ouest de l'Inde.
Les premiers carrés magiques d'ordres 5 et 6 apparurent dans une encyclopédie publiée à Bagdad vers 983, l’Encyclopédie de la Fraternité de la pureté (Rasa'il Ikhwan al-Safa)[3].
Au XIIIe siècle, le mathématicien chinois Yang Hui (杨辉 / 楊輝, , 1238-1298), qui a également défini le triangle de Pascal, travaille sur une approche structurelle du carré magique d'ordre 3.
Le mathématicien français Claude-Gaspard Bachet de Méziriac décrit une méthode pour résoudre le problème du carré magique en prenant pour exemple un caviste qui veut ranger des bouteilles dans un casier de 3 × 3 cases, dans ses Problèmes plaisants et délectables qui se font par les nombres, publié en 1612[4].
Le mathématicien suisse Leonhard Euler (1707-1783) crée ou au moins cite le « carré latin »[5], tableau carré de n lignes et n colonnes remplies de n éléments distincts dont chaque ligne et chaque colonne ne contient qu'un seul exemplaire.
Dans l'hebdomadaire pour la jeunesse Le Petit Français illustré (numéro 7 du , p. 92), sous le titre général « Problèmes amusants » est proposé le jeu suivant : « Disposer les 9 chiffres, 1, 2, 3, 4, 5, 6, 7, 8, 9, dans les 9 cases de la figure ci-dessous, de telle façon que le total des 3 chiffres de chaque ligne verticale, horizontale et diagonale soit égal à 15. »
En 1892, en France, dans le quotidien monarchiste Le Siècle, apparaît la plus ancienne grille connue de sudoku[6]. Le , toujours en France, le quotidien La France publie une autre grille de ce jeu sur une grille de 9 × 9 cases, appelé « Carré magique diabolique », et réalisé par M. B. Meyniel.
La version moderne du sudoku est inventée anonymement par l'Américain Howard Garns et publié pour la première fois en 1979 dans Dell Magazines sous le nom Number Place[7].
En , Maki Kaji (鍜治 真起, 1951-2021[8]), directeur de la société Nikoli, publie pour la première fois, dans sa revue mensuelle « Getsukan Nikoli suto » (月刊ニコリスト), le jeu Number Place sous le nom « Sūji wa dokushin ni kagiru » (数字は独身に限る), plus tard « Sūdoku » (数独)[2].
Règles de base
La grille de jeu présentée à droite, à titre d’exemple, est un carré de neuf cases de côté, subdivisé en autant de sous-grilles carrées identiques, appelées « régions ».
La règle du jeu générique, donnée en début d’article, se traduit ici simplement : chaque ligne, colonne et région ne doit contenir qu’une seule fois tous les chiffres de un à neuf. Formulé autrement, chacun de ces ensembles doit contenir tous les chiffres de un à neuf.
Une règle non écrite mais communément admise veut également qu’une bonne grille de sudoku, une grille valide, ne doit présenter qu’une et une seule solution. Ce n’est pas toujours le cas…
Les chiffres ne sont utilisés que par convention, les relations arithmétiques entre eux ne servant pas (sauf dans la variante Killer Su Doku, voir ci-après). N’importe quel ensemble de signes distincts — lettres, formes, couleurs, symboles — peut être utilisé sans changer les règles du jeu. Dell Magazines, le premier à publier des grilles, a utilisé des chiffres dans ses publications. Par contre, Scramblets, de Penny Press, et Sudoku Word, de Knight Features Syndicate, utilisent tous les deux des lettres.
L’intérêt du jeu réside dans la simplicité de ses règles, et dans la complexité de ses solutions. Les grilles publiées ont souvent un niveau de difficulté indicatif. L’éditeur peut aussi indiquer un temps de résolution probable. Quoiqu’en général les grilles contenant le plus de chiffres pré-remplis soient les plus simples, l’inverse n’est pas systématiquement vrai. La véritable difficulté du jeu réside plutôt dans la difficulté de trouver la suite exacte des chiffres à ajouter.
Ce jeu a déjà inspiré plusieurs versions électroniques qui apportent un intérêt différent à la résolution des grilles de sudoku. Sa forme en grille et son utilisation ludique le rapprochent d’autres casse-tête publiés dans les journaux, tels les mots croisés et les problèmes d’échecs. Le niveau de difficulté peut être adapté, et des grilles sont publiées dans des journaux, mais peuvent aussi être créées à la demande sur Internet.
Variantes

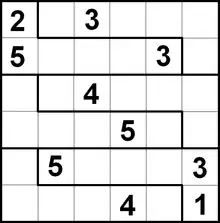


Bien que les grilles classiques soient les plus communes, plusieurs variantes existent comme :
- 2×2 ou « Sudoku binaire », contenant des régions 1×1 (version pleine d’ironie) ;
- 4×4 contenant des régions 2×2 (généralement pour les enfants) ;
- 5×5 contenant des régions en forme de pentamino ont été publiés sous le nom Logi-5;
- 6×6 contenant des régions 2×3 (proposée lors du World Puzzle Championship) ;
- 7×7 avec six régions en forme d’hexamino et une région disjointe (proposée lors du World Puzzle Championship) ;
- 9×9 avec des régions en forme de ennéamino ;
- 16×16 avec des régions 4×4 (appelées Number Place Challenger et publiées par Dell, ou appelées parfois Super Sudoku), (ou encore Sudoku Hexadécimal utilisant une notation en base 16 (Chiffre de 0 à 9 + lettres de A à F) ;
- 25×25 avec des régions 5×5 (appelées Sudoku the Giant et publiées par Nikoli) ;
- une variante impose de plus que les chiffres dans les diagonales principales soient uniques. Le Number Place Challenger, mentionné précédemment, et le Sudoku X du Daily Mail, une grille 6×6, appartiennent à cette catégorie ;
- 8×8 contenant des régions 2×4 et 4×2, et où les rangées, les colonnes, régions et les diagonales principales contiennent un chiffre unique ;
- une méta-grille composée de cinq grilles 9×9 en quinconce qui se chevauchent aux coins est publiée au Japon sous le nom de Gattai 5 (qui signifie « cinq fusionnés ») ou Samuraï. Dans le journal The Times, cette forme est appelée le Samurai Su Doku ;
- des grilles à régions rectangulaires : si une région est de dimensions L×C cases, la grille globale se décompose en C×L régions ; les valeurs à remplir vont alors de 1 à C×L ;
- Dion Church a créé une grille 3D, que le Daily Telegraph a publiée en . Le logiciel ksudoku appelle de telle grilles roxdoku et les crée automatiquement ;
- En 2006, Aurélie Delbèque et Olivier Delbeke ont publié la première grille 3D en 8×8×8, ils l’ont appelé Kuboku[9] ;
- le kamaji est une dérivation récente de sudoku basé sur le principe des sommes de chiffres ;
- irrégulier, avec des formats différents (aussi appelés Suguru ou Tectonic).
Au Japon, d’autres variantes sont publiées. En voici une liste incomplète :
- Grilles connectées séquentiellement : plusieurs grilles 9×9 sont résolues consécutivement, mais seule la première a suffisamment de dévoilés pour permettre de résoudre logiquement. Une fois résolue, certains chiffres sont copiés vers le suivant. Cette formule impose au joueur de faire des allers et des retours entre des grilles partiellement résolues.
- Grilles très grandes qui consistent en de multiples grilles qui se chevauchent (habituellement 9×9). Des grilles constituées de 20 à 50, ou plus, sont courantes. La taille des régions qui se chevauchent varie (deux grilles 9×9 peuvent partager 9, 18 ou 36 cellules). Souvent, il n’y a aucun dévoilé dans ces régions.
- Grilles habituelles où un chiffre est membre de quatre groupes, au lieu des trois habituels (rangées, colonnes et régions) : les chiffres situés aux mêmes positions relatives dans une région ne doivent pas correspondre. Ces grilles sont habituellement imprimées en couleur, chaque groupe disjoint partageant une couleur pour faciliter la lecture.
La trousse de jeux pour participer au World Puzzle Championship de 2005 contient une variante intitulée Digital Number Place : plutôt que de contenir des dévoilés, la plupart des cellules contiennent un chiffre partiellement dessiné qui emprunte à la graphie de l’affichage à sept segments.
Le , The Times a entamé la publication du Killer Su Doku, aussi nommé Samunamupure (qui signifie « lieu de sommation »), lequel indique la somme de cellules regroupées et ne révèle aucune case, ce qui ajoute un supplément de difficulté dans la recherche de la solution, bien que cela puisse aider à résoudre. Les autres règles s’appliquent.
Variantes alphabétiques
Des variantes alphabétiques, qui utilisent des lettres plutôt que des chiffres, sont aussi publiées. The Guardian les appelle Godoku et les qualifie de démoniaques. Knight Features lui préfère le terme Sudoku Word[10]. Le Wordoku[11] de Top Notch dévoile les lettres, dans le désordre, d’un mot qui court du coin gauche supérieur au coin droit inférieur. Un joueur ayant une bonne culture peut le trouver et utiliser sa découverte pour avancer vers la solution.
En français, cette variante alphabétique porte divers noms comme Sudoku lettres, Mokitu (Télé 7 jours) ou Mysmo (Libération). Certaines grilles se limitent aux mots ne comportant que des lettres différentes. D’autres acceptent des mots comportant plusieurs fois la même lettre auquel cas elle a à chaque fois une graphie différente, par exemple : MAHaRADJa. Le Custom Sudoku[12] créé par Miguel Palomo admet par contre un mot avec de vraies lettres répétées.
Le Code Doku[13] conçu par Steve Schaefer contient une phrase complète, alors que le Super Wordoku[14] de Top Notch contient deux mots de neuf lettres, chacun se trouvant sur l’une des diagonales principales. Ces jeux ne sont pas considérés comme de vrais sudokus par les puristes, car la logique n’est pas suffisante pour les résoudre, même s’ils ont une solution unique. Top Notch affirme que ces jeux sont conçus de façon à bloquer les solutions composées par des logiciels de résolution automatique.
Précurseurs du Sudoku
Un ancêtre du sudoku : le carré latin magique

Les expériences agronomiques en champ, généralement constituées d’un certain nombre de parcelles carrées ou rectangulaires, sont souvent organisées sous la forme de blocs aléatoires complets, c’est-à-dire de groupes de parcelles voisines au sein desquels les différents éléments à comparer (différentes fumures par exemple) sont tous présents et répartis au hasard.
Quand le nombre total de parcelles disponibles est égal à un carré (16, 25, 36, etc.), une autre possibilité correspond à la notion de carré latin, qui est tel que les différents éléments à comparer sont présents dans chacune des lignes et dans chacune des colonnes de parcelles.
La superposition de ces deux dispositifs peut donner naissance à ce qui a été appelé carré latin magique, notamment par W.T. Federer[15] en 1955. Dans l’exemple présenté ci-contre, chacun des six éléments étudiés (par exemple six fumures différentes) est présent dans chacun des six blocs de 2 × 3 parcelles, dans chacune des six lignes et dans chacune des six colonnes. Il s’agit strictement d’un sudoku 6 × 6.
Le sudoku classique n’est donc rien d’autre qu’un carré latin magique 9 × 9[16].
Emplois historiques des carrés magiques
Un des ancêtres du sudoku dans l'Antiquité était un carré de neuf cases à remplir par trois lettres (A, B et C) sans qu’une même lettre apparaisse deux fois dans la même colonne, ligne ou diagonale.
Les plus anciens « carrés magiques » numériques connus se trouvent en Chine (nommé Luoshu 洛书, le livre de la rivière Luo) où les chiffres étaient représentés par différentes formes géométriques contenant n ronds[17] (vers -300), et en Inde où furent inventés ce que nous appelons les chiffres arabes. Ils ont à l’origine des significations divinatoires.
Au Moyen Âge, ce sont les arabes qui au Xe siècle auraient donné les premiers une application purement mathématique et non plus sacrée aux carrés magiques.
Pendant la Renaissance, Cornelius Agrippa (1486-1535), utilise des carrés magiques toujours dans un but ésotérique.
Le mathématicien français Pierre de Fermat (1601 (ou 1607)-1665) travailla sur les carrés magiques et les étendit aux cubes magiques.
En 1691 Simon de La Loubère explique le fonctionnement du carré magique utilisé au Siam, dans son ouvrage Du Royaume de Siam, où celui-ci possède une fonction sacrée.
Le problème des officiers

En 1782, le mathématicien suisse Leonhard Euler imagine un problème dans une grille. Certains attribuent donc la paternité du sudoku au Suisse, bien que les travaux d’Euler concernent les carrés latins et la théorie des graphes.
On considère six régiments différents, chaque régiment possède six officiers de grades distincts. On se demande maintenant comment placer les 36 officiers dans une grille de 6×6, à raison d’un officier par case, de telle manière que chaque ligne et chaque colonne contienne tous les grades et tous les régiments.
Il s’agit en d’autres termes d’un carré gréco-latin d’ordre 6 (la combinaison de deux carrés latins, un carré latin pour les régiments, un carré latin pour les grades), problème dont la résolution est impossible. Euler l’avait déjà pressenti à l’époque, sans toutefois donner une démonstration formelle à sa conjecture. Il dira :
« Or, après toutes les peines qu’on s’est données pour résoudre ce problème, on a été obligé de reconnaître qu’un tel arrangement est absolument impossible, quoiqu’on ne puisse pas en donner de démonstration rigoureuse. »
En 1901, le Français Gaston Tarry démontre l’impossibilité du résultat grâce à une recherche exhaustive des cas et par croisement des résultats.
Le lien entre le sudoku et le problème des 36 officiers est la contrainte qui empêche la répétition du même élément dans la grille, tout en arrivant finalement à un jeu qui emploie le principe du carré latin (combinaison de deux carrés latins dans le cas du carré gréco-latin, carré latin subdivisé en plusieurs régions dans le cas du sudoku).
Version moderne du sudoku
Le sudoku a des ancêtres français qui remontent à 1895. Le jeu n’est apparemment pas une invention récente comme beaucoup le pensaient. À la fin du XIXe siècle, les Français jouaient en effet à remplir des grilles 9×9 divisées en 9 régions, très proches de ce jeu (mais les grilles initiales comprenaient des contraintes supplémentaires sur la solution), qui étaient publiées dans les grands quotidiens de l’époque, révèle Pour la science dans son édition de .
Selon le magazine, la grille la plus proche d’un sudoku, qui a été retrouvée par le Français Christian Boyer, est celle de B. Meyniel, publiée dans le quotidien La France du . Une variante proche avait été publiée peu avant, en , dans Le Siècle, variante qui utilisait des nombres à deux chiffres[18].
En 1979, un pigiste spécialisé dans les casse-tête, Howard Garns, crée le premier jeu tel que nous le connaissons aujourd’hui. Dell Magazines l’introduit cette même année dans une publication destinée au marché new-yorkais, le Dell Pencil Puzzles and Word Games, sous le nom de Number Place. Nikoli l’introduit au Japon en dans le magazine Monthly Nikolist.
En 1986, Nikoli introduit deux nouveautés, qui rendront le jeu populaire : les cases dévoilées sont symétriquement distribuées autour du centre de la grille et leur nombre est au plus de 30. Cependant, on ignore toujours à cette époque les autres symétries possibles sur la grille dont l’axe de symétrie est l’une des deux diagonales ou des deux médianes (la colonne et la ligne centrales). Aujourd’hui, la plupart des journaux importants au Japon, tel Asahi Shimbun, publient le jeu sous cette forme de symétrie centrale. Mais en dépit de cet aspect esthétique, les grilles sont généralement de mauvaise qualité, car les trois propriétés concernant la symétrie, l’unicité de la solution et l’irréductibilité ne peuvent être réalisées facilement en même temps !
En 1989, Loadstar et Softdisk publient DigitHunt pour le Commodore 64, probablement le premier logiciel pour ordinateur personnel à créer des Sudoku. Une entreprise continue d’utiliser ce nom.
En 1995, Yoshimitsu Kanai publie un générateur logiciel sous le nom de Single Number (traduction anglaise de Sudoku), pour le Macintosh, en japonais et en anglais[19] et, en 1996, il récidive pour Palm OS[20].
En 2005, Dell Magazines publie également deux magazines dédiés aux Sudoku : Original Sudoku et Extreme Sudoku. De plus, Kappa Publishing Group reprend les grilles de Nikoli dans GAMES Magazine sous le nom de Squared Away. Les journaux New York Post, USA Today et San Francisco Chronicle publient aussi ce jeu. Des grilles apparaissent dans certaines anthologies de jeux, telles que The Giant 1001 Puzzle Book (sous le nom de Nine Numbers).
C’est en que le sudoku, publié par Sport cérébral, éditeur spécialisé dans les jeux de réflexion, arrive en France. Le premier numéro se vendra à 20 000 exemplaires, soit deux fois plus qu’à l’accoutumée lors de la sortie d’un nouveau jeu — un record, selon Xavier de Bure, directeur général de l’éditeur. La Provence publie les premières grilles quotidiennes le , suivi au cours de l’été 2005 par Le Figaro, Libération, Nice-Matin, 20 Minutes, Métro et Le Monde. Le magazine 1, 2, 3… Sudoku sortit son premier numéro en .
Le phénomène a également gagné la Suisse, Wayne Gould fournit des grilles au quotidien francophone Le Matin qui a vendu cette année-là 150 000 livres de sudoku. Le Temps, autre quotidien helvétique publie quant à lui des grilles de sudoku depuis .
Popularité dans les médias
Dès 1997, Wayne Gould, un Néo-Zélandais et juge à la retraite de Hong Kong, est intrigué par une grille partiellement remplie dans une librairie japonaise. Pendant six ans, il développe un programme qui crée automatiquement ces grilles. Sachant que les journaux britanniques publient des mots croisés et autres jeux semblables depuis longtemps, il promeut le sudoku auprès du journal The Times, lequel publie pour la première fois une grille le .
Trois jours plus tard, The Daily Mail publie aussi une grille sous le nom Codenumber. The Daily Telegraph introduit sa première grille le , suivi par les autres publications du Telegraph Group. Le , le Daily Telegraph de Sydney publie pour la première fois une grille.
C’est lorsque le Daily Telegraph publie des grilles sur une base quotidienne, à partir du , tout en promouvant celui-ci sur sa page une, que les autres journaux britanniques commencent à y prêter attention. Le Daily Telegraph a continué sa campagne de promotion lorsqu’il a réalisé que ses ventes augmentaient simplement par la présence d’une grille de sudoku. The Times était plutôt discret sur l’immense popularité qui entourait son concours de sudoku. Il avait déjà prévu de tirer avantage de son avance en publiant un premier livre sur le sudoku.
En avril et , le jeu était suffisamment populaire pour que plusieurs journaux nationaux le publient sur une base régulière. Au nombre de ceux-ci, on retrouve The Independent, The Guardian, The Sun (intitulé Sun Doku) et The Daily Mirror. Lorsque le mot Sudoku devient populaire au Royaume-Uni, le Daily Mail l’adopte à la place de Codenumber. Dès lors, les journaux ont rivalisé d’imagination pour pousser leurs grilles. The Times et Daily Mail affirment qu’ils sont les premiers à avoir publié une grille de sudoku, alors que The Guardian affirme, ironiquement, que ses grilles construites à la main, obtenues de Nikoli, apportent une meilleure expérience que les grilles créées à l’aide d’un logiciel.
La subite popularité du sudoku au Royaume-Uni a attiré son lot de commentaires dans les médias (voir Liens externes ci-dessous) et des parodies ont suivi, par exemple la section G2 du journal The Guardian s’annonce comme le premier supplément avec une grille par page[21]. Le sudoku est devenu particulièrement visible tout de suite après les élections de 2005 au Royaume-Uni, incitant quelques commentateurs à affirmer qu’il remplissait un besoin chez le lectorat politique. Une autre explication suggère qu’il attire et retient l’attention des lecteurs, plusieurs se sentant de plus en plus satisfaits lorsque la solution se dessine. The Times estime que les lecteurs apprécient à la fois les grilles faciles et difficiles. En conséquence, il les publie côte à côte depuis le .
La télévision britannique s’est empressée de surfer sur la vague de popularité et Sky One diffuse la première émission sur le sudoku, Sudoku Live, le , que la mathématicienne Carol Vorderman présente. Neuf équipes de neuf joueurs, dont une vedette, chacune représentant une région géographique, tentent de compléter une grille de sudoku. Chaque joueur a en main un appareil qui lui permet de saisir un chiffre dans l’une des quatre cellules dont il est responsable. Échanger avec les autres membres de l’équipe est permis mais, la familiarité manquant, les compétiteurs ne le font pas. Également, l’auditoire à la maison participe à une autre compétition interactive en même temps. Sky One a tenté de créer un engouement[22] pour son émission par le biais d’une énorme grille de 84 m de côté. Cependant, il avait 1 905 solutions.
Cette brusque augmentation de popularité dans les journaux britanniques et internationaux fait que le sudoku est considéré comme le « cube de Rubik du XXIe siècle » (traduction libre de « the Rubik's cube of the 21st century »). À titre d’exemple, Wayne Gould fournit fin 2005 des grilles pour environ 70 quotidiens dans 27 pays. Le développement de cette société a été financé en partie par le gouvernement britannique qui y voit un moyen de prévention des maladies séniles (Alzheimer en particulier).
Le , la Télévision suisse romande lance une émission télévisée quotidienne, Su/do/ku, où deux candidats s’affrontent sur 5 jours, à raison de 3 manches de 8 minutes chaque jour. Toutefois, la difficulté pour faire passer ce genre de jeu à la télévision entraînera l’arrêt de l’émission après quelques semaines.
Des championnats nationaux sont également organisés comme le 1er championnat de France de sudoku (Paris, ) remporté par AntFal, 19 ans. Cette compétition organisée par Sport cérébral récompense le meilleur joueur de l’année. C’est l’agence de communication Décollage vertical qui a mis en place cet événement unique en France. Depuis, de nombreux autres tournois ont été organisés en France.
Mathématiques
Structure logique
Le problème de placer des chiffres sur une grille de n²×n² comprenant n×n régions est prouvé NP-complet[23].
Le problème de la résolution de tout sudoku peut être formalisé de façon équivalente par un problème de coloration de graphe : le but, dans la version classique du jeu, est d’appliquer 9 couleurs sur un graphe donné, à partir d’un coloriage partiel (la configuration initiale de la grille). Ce graphe possède 81 sommets, un par cellule. Chacune des cases du sudoku peut être étiquetée avec un couple ordonné (x, y), où x et y sont des entiers compris entre 1 et 9. Deux sommets distincts étiquetés par (x, y) et (x’, y’) sont reliés par une arête si et seulement si :
- x = x’ (les deux cellules appartiennent à la même ligne) ou,
- y = y’ (les deux cellules appartiennent à la même colonne) ou,
- et (les deux cellules appartiennent à la même région). La grille se complète en affectant un entier entre 1 et 9 pour chaque sommet, de façon que tous les sommets liés par une arête ne partagent pas le même entier.
Une grille solution est aussi un carré latin. La relation entre les deux théories est désormais complètement connue, depuis que D. Berthier a démontré, dans The Hidden Logic of Sudoku[24], qu’une formule logique du premier ordre qui ne mentionne pas les blocs (ou régions) est valide pour le sudoku si et seulement si elle est valide pour les carrés latins.
Il y a notablement moins de grilles solutions que de carrés latins, car le sudoku impose des contraintes supplémentaires (Voir ci-dessus nombre de grilles complètes possibles).
Le nombre maximum de dévoilés sans qu’une solution unique apparaisse immédiatement, peu importe la variante, est la taille de la grille moins 4 : si deux paires de candidats ne sont pas inscrits et que les cellules vides occupent les coins d’un rectangle, et qu'exactement deux cellules sont dans une région, alors il existe deux façons d’inscrire les candidats. L’opposé de ce problème, à savoir le nombre minimum de dévoilés pour garantir une solution unique, est un problème non résolu, bien que des enthousiastes japonais aient découvert une grille 9×9 sans symétrie qui contient seulement 17 dévoilés[25] - [26], alors que 18 est le nombre minimum de dévoilés pour les grilles 9×9 symétriques.
Symétries des grilles
Gordon Royle considère que deux grilles complètes doivent être considérées comme équivalentes si elles peuvent être transformées l’une en l’autre (ou l’inverse) grâce à une combinaison quelconque des opérations suivantes :
- échange des lignes avec les colonnes (transposition - deux solutions)
- permutations des 9 nombres (9! solutions)
- permutation des trois lignes au sein d'un même bloc (3!³ solutions) ou des trois colonnes (3!³ solutions)
- permutation des trois blocs sur une ligne de blocs (3! solutions) ou sur une colonne de blocs (3! solutions)
Une grille complète permet ainsi de créer un total de 2×9!×(3!)^8 = 1 218 998 108 160 grilles essentiellement équivalentes. On remarque l’analogie avec les opérations matricielles en algèbre linéaire.
Nombre de grilles complètes
Il est évident que le nombre de grilles complètes est inférieur au nombre de façons de placer neuf chiffres 1, neuf chiffres 2…, neuf chiffres 9 dans une grille de 81 cases. Le nombre de grilles est donc très inférieur à
En effet, dans ce décompte, on ne tient compte d’aucune des contraintes d’unicité.
Le nombre de grilles complètes possibles est également inférieur au nombre de carrés latins de côté 9.
Enfin, le nombre de grilles complètes possibles est inférieur à qui correspond au nombre de façons de construire les régions sans tenir compte des contraintes sur les lignes et les colonnes.
En 2005, Bertram Felgenhauer et Frazer Jarvis ont prouvé[27] que ce nombre de grilles était de[27] - [28] - [29] :
Ce nombre est égal à :
- 9!×722×27×27 704 267 971
Le dernier facteur est un nombre premier. Ce résultat a été prouvé grâce à une recherche exhaustive. Frazer Jarvis a ensuite considérablement simplifié la preuve grâce à une analyse détaillée. La démonstration a été validée de manière indépendante par Ed Russell. Jarvis et Russell ont par la suite montré qu’en tenant compte des symétries, il y avait 5 472 730 538 solutions[30] - [29]. Un catalogue complet de ces grilles a été constitué.
Nombre de grilles incomplètes
Quant au problème suivant, il semble non résolu : si on s’intéresse au nombre de problèmes proposables, ce nombre est inconnu ; en revanche, on sait qu’il est nettement plus important que le nombre indiqué ci-dessus car il existe de très nombreuses façons de présenter des grilles initiales dont la solution (unique) conduit à la même grille terminée (complète). En effet, partant d'une grille complète, on peut construire un problème proposable par la méthode suivante :
- au départ, aucune case de la grille complète n'est « nécessaire » ;
- choisir une case non « nécessaire » quelconque. Si la suppression de la case choisie conduit à une grille à plusieurs solutions, la marquer comme « nécessaire », sinon la supprimer ;
- si toutes les cases remplies sont « nécessaires », la grille incomplète est un problème proposable ; sinon réitérer l'étape précédente.
On voit facilement que dans les premières étapes, aucune case n'est réellement nécessaire, ce qui permet d'imposer un problème différent d'un problème « proposable » donné, simplement en vidant une des cases qui était fournie dans ce problème.
Il est facile de montrer, sur certains exemples de grilles complètes, à quel point on peut, pour une même grille complète, présenter des grilles initiales de difficultés tout à fait contrastées, depuis les grilles pour débutants jusqu’aux grilles dites diaboliques ; il est en tout cas très facile, connaissant une grille initiale diabolique, de fabriquer une grille pour débutant dont la solution unique complète soit identique à celle de la grille diabolique choisie !
Cependant, il existe désormais une estimation (basée sur une approche statistique) du nombre total de problèmes minimaux (voir la section « classification des problèmes »).
Nombre minimal de révélés

Un révélé étant une case dont le contenu est visible sur une grille de sudoku, se pose le problème de leur nombre minimal.
Le nombre maximal de « révélés » dans une grille qui ne fournisse pas une solution unique est une grille complète moins quatre : si dans une grille complète deux occurrences de deux nombres sont supprimées, et que ces occurrences sont aux angles d'un rectangle, et que deux de ces cellules sont dans un même groupe, alors il y a deux solutions pour compléter la grille. Ceci étant une caractéristique générale des carrés latins, la plupart des grilles de sudoku ont le même maximum.
Le problème de savoir combien de cases initiales remplies sont nécessaires pour conduire à une solution unique est, à ce jour, sans réponse sûre. Le meilleur résultat, obtenu par des Japonais, est de 17 cases sans contrainte de symétrie[31] - [32]. Aujourd’hui on sait qu’il existe un très grand nombre de problèmes comportant 17 révélés (voir un exemple ci-contre avec sa solution).
Rien ne dit que ce ne soit pas possible avec moins de nombres. D'après un article de Gary McGuire publié dans le site de prépublication ArXiv il n'est pas possible d’en définir un ne comportant que 16 révélés et ayant une solution unique[33] - [34] - [29].
Autre problème non résolu : à cette date, aucun résultat n’existe sur le nombre de grilles complètes dans un super sudoku (grille 16 × 16).
Méthodes de résolution utilisées par les joueurs
Remarques préliminaires
- Il existe de nombreuses approches de la résolution des Sudokus, dont certaines ne sont praticables que par ordinateur. Il ne sera question ici que des méthodes utilisées par les joueurs.
- Il ne s’agit pas de donner une liste exhaustive de ces méthodes (ce qui nécessiterait un livre volumineux), mais un simple aperçu. De nombreuses variantes et extensions existent, comme les poissons à nageoires (finned fish), trop spécialisées pour être détaillées ici.
- Quelles sont les méthodes de résolution admissibles par un joueur ? Toute réponse à cette question aurait une composante subjective ; ne pas reconnaître d’emblée ce fait conduirait à des querelles stériles. La plupart des joueurs refusent les essais et erreurs, ou hypothèses.
- Il existe un site de référence, Sudopedia, présentant de manière consensuelle le vocabulaire standard du Sudoku et les règles de résolution les plus connues. En anglais uniquement, il fonctionne selon les mêmes principes que Wikipedia.
- La méthode la plus rapide pour un ordinateur consiste à essayer systématiquement, l’un après l’autre, tous les candidats restants. Appliquée récursivement, elle peut résoudre tous les problèmes. Mais cette méthode, fort peu élégante, est rejetée par quasiment tous les joueurs. Tout au plus est-elle acceptée comme ultime recours, quand plus rien d’autre ne marche.
Pour de nombreuses méthodes, la discussion se fait sur l'appartenance à une « région » qui peut être (par définition) indifféremment une ligne, une colonne, ou un groupe.
Principe
À un niveau élémentaire, il faut balayer la grille pour chaque chiffre de un à neuf, et pour chaque bloc :
- Regarder si le chiffre y figure ou pas ;
- Si le chiffre y figure, regarder quelles sont les cases qu'il interdit sur les autres blocs en ligne ou en colonne ;
- Si le chiffre n'y figure pas, regarder quelles sont les cases où il ne peut pas figurer, compte tenu de la position des autres instances du même chiffre dans les autres blocs en ligne ou en colonne.
Lorsqu'il n'y a qu'une seule possibilité pour une ligne, une colonne, ou un bloc, c'est nécessairement là que le chiffre doit s'inscrire. Avec un peu d'expérience, il est possible de visualiser les cases « allumées » sur l'ensemble de la grille, où ce chiffre peut figurer, ce qui permet de détecter des configurations plus avancées.
Quand un problème peut être résolu en n’utilisant que les règles élémentaires de cette section, des joueurs expérimentés peuvent se dispenser de l’écriture explicite des candidats. Ces problèmes correspondent à des niveaux « facile » ou « élémentaire ».
Singleton
Le « singleton » correspond au cas trivial où il n'y a plus qu'une seule cellule vide dans une « région » (ligne, colonne ou bloc). Dans ce cas, la valeur de la cellule est évidemment le seul nombre manquant dans la région : c'est à la fois le seul endroit où le nombre manquant puisse être mis (singleton caché), et c'est la seule valeur que peut recevoir la cellule vide (singleton nu).
Cette configuration se rencontre surtout en fin de problème, quand presque toutes les cellules ont été remplies.
Plus généralement, le « singleton » correspond au cas où il n'y a (localement) qu'une seule solution : une case ne peut recevoir qu'une seule valeur (singleton nu), ou bien une valeur ne peut être affectée qu'à une seule case (singleton caché), tout autre choix conduisant à une incohérence immédiate. Il s'oppose aux « paires », « triplets » et « quadruplets », où la discussion porte sur plusieurs valeurs simultanément.
Élimination directe - Singleton caché

La recherche d'un « singleton caché » revient à se poser la question « Dans cette région (ligne, colonne ou bloc), quelles sont les cases qui peuvent accueillir un 1 (2 ou 3 ou… 9) ? » : si la position est unique dans la région considérée, alors le candidat devient valeur en cette position.
La recherche de singleton caché est d'autant plus facile que la valeur est fréquente dans la grille : les contraintes de positionnement augmentent, alors que le nombre de positions possibles diminue.
Le marquage des cellules n'apporte qu'une faible plus-value pour la recherche des singletons cachés : il faut de toute manière balayer toute la région pour vérifier que la valeur recherchée n'y figure qu'une seule fois comme candidat. C'est pour cette raison que ces singletons sont qualifiés de « cachés ».
Inversement, le « singleton caché » est souvent facilement révélé par un balayage systématique des chiffres et des blocs, parce que sa position ne dépend que de la position du chiffre considéré dans les blocs voisins, et de ce que les cases sont libres ou occupées dans le bloc considéré. Dans l'exemple ci-contre, quand on en est à estimer les possibilités du « 4 » pour le bloc supérieur droit, la seule information nécessaire pour les cases du « 7 » et du « 8 » est qu'elles sont occupées par des chiffres différents de 4 ; la conclusion est la même quel que le soit le chiffre contenu dans ces cases.
Élimination indirecte
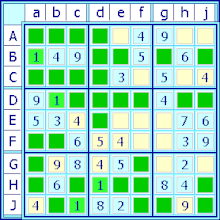
L'élimination indirecte est un prolongement de l'élimination directe.
Lorsqu'on balaye la grille pour localiser les cases admissibles pour un certain candidat, on peut se trouver dans la situation où dans un bloc, les cases admissibles sont toutes localisées sur une même ligne (ou une même colonne). Dans ce cas, quelle que soit la position finale du candidat dans le bloc, cet alignement interdit pour le candidat les autres cases libres de cette même ligne (ou colonne) situées dans les autres blocs. Autrement dit : si dans un bloc, les candidats sont sur une même ligne, le candidat est exclu des autres cases libres de la ligne.
De même, quand dans deux blocs en ligne, les candidats sont limités à deux lignes, les candidats du troisième bloc ne peuvent se trouver que sur la troisième ligne (et réciproquement pour les colonnes).
Cette interdiction peut conduire à identifier un singleton caché, comme dans le premier exemple ci-contre. Elle peut également, de manière plus subtile, conduire à conclure que dans un autre bloc de cette ligne (ou colonne), les candidats ne peuvent se situer que sur un même ligne ou colonne, conduisant de proche en proche à une élimination indirecte en chaîne. Cette première application de l'élimination indirecte peut par conséquent se faire sans marquage, mais demande plus de réflexion.

Dans l'exemple ci-contre, après que les paires identifiables ont été marquées, l'examen du candidat "1" permet par exemple d'identifier deux singletons, en enchaînant quatre éliminations indirectes. Il n'y a qu'un seul "1" dans la cellule "Aa", ce qui interdit la présence d'un autre "1" en ligne "A" et en colonne "a" (en jaune).
- On commence par raisonner sur les blocs de la verticale centrale pour faire deux éliminations indirectes :
- Dans le bloc supérieur central, il ne peut donc y avoir de "1" que sur la colonne "d" (en vert), excluant ce même candidat sur le reste de la colonne.
- Par conséquent, dans le bloc inférieur central, le "1" ne peut se trouver que sur la colonne "e", excluant ce même candidat sur le reste de la colonne.
- Et donc, dans le bloc central, le candidat "1" ne peut se trouver que sur la colonne "f" (en bleu).
- On raisonne à présent sur les blocs de l'horizontale centrale pour une élimination indirecte sur deux lignes :
- Dans le bloc central, "1" ne peut que se trouver sur les lignes "E&F" (en bleu).
- Mais dans le bloc de centre gauche, le "1" est restreint à ces mêmes lignes "E&F" (en vert).
- Par conséquent, dans le bloc de centre droit, le "1" se trouve nécessairement sur la ligne "D" (en bleu).
- De là, on examine les blocs de droite pour une seconde élimination sur deux lignes :
- Dans le bloc de centre droit, le "1" est à présent restreint aux colonnes "h&j" (en bleu).
- Mais dans le bloc supérieur droit, le "1" est également restreint à ces mêmes colonnes (en vert).
- Donc, dans le bloc inférieur droit, le "1" ne peut pas se trouver dans les colonnes "h&j" (en jaune).
- On voit à présent que sur la ligne "J", les deux cellules qui avaient été marquées des paires "12" et "13" ne peuvent donc pas recevoir un "1" ; leur valeur est donc nécessairement "2" et "3".
Principe
La deuxième méthode de balayage consiste à se demander, sur un groupe donné (ligne, colonne ou bloc) : (1) quels sont les manquants, et (2) où peuvent-ils se trouver. L'objet est d'identifier des « singletons cachés », et à défaut, des paires à marquer.
Cette méthode est particulièrement triviale dans le cas où il ne manque qu'un seul chiffre dans l'entité, dans ce cas la case est un « singleton », à la fois un « singleton nu » et un « singleton caché », et sa solution est immédiate.
Elle est d'autant plus fructueuse qu'il y a plus de cases remplies sur l'entité considérée. Elle peut donc être faite d'office dès qu'une entité n'a plus que deux cases vides (inscription directe des paires), puis, par ordre de préférence, quand une entité n'a plus que trois, quatre, voire cinq cases vides. Un balayage à « six cases vides » ne donnera des fruits qu'exceptionnellement (mais peut en donner).
Singleton nu

Si une cellule n'accepte qu'un unique candidat, alors c’est la valeur de cette cellule. C'est ce que l'on appelle un « singleton nu ». Le cas a d'autant plus de chance de se produire que la cellule examinée se trouve à l'intersection de régions assez remplies, ce qui augmente les contraintes et restreint le nombre de valeurs possibles sur la cellule examinée.
Cette appellation de « singleton nu » vient de ce que dans les logiciels d'aide à la résolution des sudoku, quand la liste des candidats est affichée sur chaque cellule, ces cases sont immédiatement visibles (nues) parce que ce sont les seules qui n'ont qu'un seul candidat (singleton)[35]. Pour l'anecdote, cette désignation de « singleton nu » (naked single, en anglais, soit littéralement « célibataire dénudé ») peut conduire certains filtres de contrôle parental à limiter l'accès aux pages de discussion du sudoku[36]…
Marquage des doublets
Dans ce type de balayage, il est utile de marquer directement les paires, c'est-à-dire les cases de la grille où il ne reste plus que deux candidats. Ces cases peuvent être remplies par le couple de chiffres, inscrits en petit ou au crayon ; et la seule évolution possible pour de telles cases est de basculer sur l'une ou l'autre de ces valeurs. L'avantage de ce marquage est double :
- Dans le balayage « élémentaire » précédent, il permet dans certains cas (quand une même paire est sur la même ligne, colonne, ou bloc) de faire comme si ces deux chiffres étaient effectivement présents sur la grille pour bloquer les possibilités associées aux autres cases.
- En fin de problème, ces cases permettent de terminer très rapidement une grille, puisque dès qu'une des valeurs de la paire est trouvée sur une autre case liée (en ligne, en colonne, ou dans le bloc), on peut immédiatement inscrire l'autre valeur comme valeur effective, sans avoir à refaire tout le raisonnement qui avait conduit initialement à limiter les possibilités à deux valeurs.
Marquage des paires
Le marquage des paires constitue le second niveau de résolution des sudokus. « Marquer une paire » sur une case donnée consiste à noter que sur cette case, il n'y a que deux candidats possibles.
Le marquage peut se faire simplement en mettant dans la case les deux chiffres candidats, mais en écriture suffisamment petite pour être oblitérée par la valeur définitive. Il n'y a qu'une seule manière d'apporter de l’information à une case portant une paire, c'est en donnant la valeur effective ; de ce fait, le marquage des paires ne conduit pas à des surcharges graphiques trop importantes.
Il est important, à ce stade, de remarquer que si le marquage direct des possibilités limitées aux paires dans une case est effectivement utile, marquer ainsi les possibilités plus étendues (trois, quatre candidats possibles,...) n'a au contraire aucun intérêt (et constitue une pratique de débutant).
Paires couplées

Lorsque les paires sont marquées, on peut rencontrer une même paire de candidats dans deux cases d'un même groupe (ligne, colonne ou bloc). Dans ce cas, les deux cases occupées par la paire sont couplées et fonctionnent comme s'ils étaient occupés par les candidats correspondants, interdisant ces deux candidats à toutes les autres cases libres de ce même groupe (ligne, colonne ou bloc).
Quelques cas particuliers sont facilement identifiables :
- Lorsqu'il ne reste plus que deux cases libres sur une ligne ou une colonne, ces deux cases forment par construction une paire nue ; et si elles sont situées dans un même bloc, elles interdisent ces valeurs au reste du bloc.
- Lorsqu'une paire couplée apparaît dans un groupe ayant trois cases libres, la troisième case n'a qu'une valeur possible : c'est un singleton nu.
- Lorsqu'une paire couplée apparaît dans un groupe ayant quatre cases libres, les deux cases restantes forment nécessairement une paire sur laquelle les deux autres valeurs restantes sont possibles : c'est une paire cachée.
La prise en compte de ces paires couplées peut conduire à noter de nouvelles paires. Dans l'exemple ci-contre, la recherche des candidats possibles a conduit notamment à identifier deux paires « 78 » sur la colonne « e ». Sur les six cases vides de la colonne, il n'y en a donc que quatre qui sont réellement libres, puisque deux peuvent être considérées comme quasi remplies.
- En recherchant où les quatre autres valeurs « 1459 » peuvent être localisées sur cette même colonne, on identifie une nouvelle paire « 14 » en ligne A, et deux paires « 59 » en lignes D et J.
- La case restante en ligne F est donc également une paire « 14 ».
Élimination indirecte
Lorsqu'on balaye la grille pour localiser les cases admissibles pour un certain candidat, on peut se trouver dans la situation où le candidat en cours d'examen figure dans une paire couplée sur une même ligne ou colonne. Dans ce cas, le candidat est exclu du reste de cette ligne (ou colonne), limitant les possibilités dans les autres blocs touchés par cette ligne (ou colonne).
Paires cachées
Les « paires cachées » demandent généralement une recherche systématique pour être détectées. Pour les détecter, il faut effectuer un balayage systématique par bloc (ligne, colonne, ou carré). Sur chaque bloc, il faut se poser la question « où sont les 1 » [...] « où sont les 9 ». Si un des chiffres ne peut être que dans deux emplacements possibles, il est possible qu'il fasse partie d'une paire cachée ; et si un autre chiffre ne peut être que dans ces deux mêmes emplacements, ces deux chiffres forment ensemble une « paire cachée ». Dans ce cas, parce que ces deux chiffres ne peuvent qu'être à ces deux emplacements, il n'est pas possible qu'un autre chiffre se trouve sur ces mêmes emplacements, ce qui élimine les possibilités correspondantes pour les autres chiffres.
La recherche des paires cachées est beaucoup plus fastidieuse, parce qu'elle porte théoriquement sur les 3x9=27 blocs, pour lesquels il faut vérifier si l'une des 9x8/2=36 paires possibles ne peut occuper que deux parmi 9 cases possibles. Il est possible d'accélérer un peu cette recherche, en remarquant d'une part que si la recherche est systématique, une fois la paire "a-b" testée il est inutile de tester la paire "b-a", et surtout, d’autre part, que si une case est déjà occupée par un doublet, une éventuelle paire cachée ne peut porter que sur ces deux mêmes éléments.
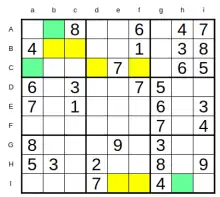
Par exemple, sur la figure ci-jointe, trois paires cachées ont été identifiées, qui permettent de remplir une case chacune :
- Les cases B-bc (jaune) sont les seules du carré supérieur gauche où peuvent être présentes les valeurs 6 et 7 ; de ce fait, le 5 n'est possible dans ce carré qu'en Ab (vert).
- Sur la ligne C, les cases C-df (jaune) sont les seules de la ligne pouvant recevoir les valeurs 4 et 8 ; de ce fait, le 3 n'est possible dans cette ligne qu'en Ca (vert).
- Sur la ligne I, les cases I-ef (jaune) sont les seules de la ligne à pouvoir recevoir les valeurs 3 et 8 ; de ce fait, le 5 n'est possible qu'en Ih (vert).
Triplets nus
Lorsqu'on recherche les manquants sur un groupe où les paires sont marquées, on peut se trouver dans la situation où le groupe affiche deux paires « ab » et « bc » ayant un élément « b » en commun. Il convient alors d'examiner si une autre case de ce groupe n'admet comme valeurs possibles que ces trois mêmes valeurs « abc ». Si c'est le cas, ces trois valeurs se répartissent nécessairement sur ces trois cases, et sont par conséquent exclues des autres cases libres du groupe :
- Si le groupe n'a que quatre cases libres, la quatrième est nécessairement un singleton.
- Si le groupe a cinq cases libres, les deux autres forment nécessairement une paire couplée.
- D'une manière générale, il devient possible de rechercher singletons et paires sur les autres cases libres du groupe, en excluant ces trois valeurs « abc ».
Gestion des nombres candidats
Ces recherches sont plus laborieuses que les précédentes, et pour les conduire systématiquement, il est plus facile de marquer les cellules. La notion de candidat n’est pas inhérente au problème du Sudoku, mais doit être introduite par le joueur pour mettre en œuvre la plupart des méthodes de résolution.
Lorsqu’un chiffre n’est pas a priori impossible dans une cellule, on dit qu’il est un candidat. Alors que les dévoilés sont les données initiales du problème, l’ensemble des candidats évolue au cours du processus de résolution. Il ne peut que diminuer ; et cela se produit lorsqu’on a démontré (par les diverses méthodes décrites plus bas) qu’un candidat est en fait impossible. Les fondements logiques formels de cette notion (qui n’est pas aussi évidente qu’il paraît) ont été définis et étudiés en détail dans La Logique cachée du Sudoku, un livre en anglais (The Hidden Logic of Sudoku[24]) ; ils font appel à la logique épistémique. L’article From Constraints to Resolution Rules, Part I: Conceptual Framework[37], librement disponible sur les pages web de son auteur, expose aussi cette logique dans le cadre général des problèmes de satisfaction de contraintes.
Il y a deux notations utilisées pour les candidats : indicée et pointée.
- Pour la notation indicée, les candidats sont inscrits dans une cellule, chaque chiffre occupant ou non une place précise. Quand un candidat est impossible, il est rayé de la liste. L’inconvénient de cette méthode est que les journaux publient des grilles de petite taille, ce qui rend difficile l’inscription de plusieurs chiffres dans une même cellule. Plusieurs joueurs reproduisent à plus grande échelle de telles grilles ou ont recours à un crayon à pointe fine.
- Pour la notation pointée, les joueurs inscrivent des points dans les cellules vides. Il y a deux logiques possibles, opposées et mutuellement exclusives :
- Quand un candidat s'avère impossible, le point correspondant est noirci. Par exemple, pour indiquer que « 1 » ne peut pas être candidat, un point est marqué en haut à gauche dans la cellule. Cette notation permet de jouer directement avec une grille imprimée dans un journal, et présente l'avantage de ne pas avoir à effacer ses marques. Cependant, elle demande du soin : il est possible de mal placer un point dans un moment d’inattention et une petite marque faite par erreur peut mener à de la confusion. Certains joueurs préfèrent utiliser un stylo pour limiter les fautes.
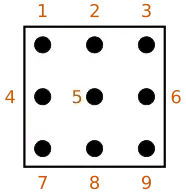
- Quand un candidat s'avère possible, le point correspondant est noirci. La position relative du point indique le chiffre manquant. Par exemple, pour représenter le chiffre 1, le joueur positionnera son point en haut à gauche de la cellule (cf schéma ci-dessus). S'il s'avère plus tard dans le raisonnement que cette hypothèse peut être éliminée, il suffira alors de barrer ce point d'une petite croix.
Lorsqu'on peut déduire qu'un nombre est nécessairement la valeur d’une cellule :
- on peut supprimer tous les autres candidats de cette cellule,
- et on peut supprimer ce nombre comme candidat de toutes les autres cellules de la même ligne, de la même colonne et du même bloc.
Élimination indirecte - interactions ligne-bloc et colonne-bloc
Lorsqu'on utilise un marquage des candidats possibles, la méthode d'élimination indirecte (mentionnée ci-dessus dans les méthodes « faciles ») se décline alors en deux cas permettant d'exclure certains candidats :
- Comme précédemment, si dans un bloc, les candidats se concentrent sur une même ligne (ou colonne), le candidat est exclu sur le reste de la ligne (ou colonne). Ce premier cas se rencontrait déjà dans les méthodes simples, parce qu'il permet parfois d'identifier un singleton caché.
- De plus à présent, si dans une ligne (ou colonne) les candidats se concentrent sur un même bloc, le candidat est exclu du reste du bloc. Ce deuxième cas ne peut jamais conduire à identifier un singleton caché.
L'élimination indirecte peut se faire formellement sur des cellules marquées, mais sa détection n'est pas tellement facilitée par le marquage.
Groupes nus et cachés
Les groupes nus et cachés correspondent à des situations assez symétriques : dans une même région (ligne, colonne ou bloc), on recherche un groupe de n (couramment de deux à quatre) nombres dont la présence est possible dans un nombre égal de cases vides et présentant une configuration remarquable, soit que la présence de ces nombres soit impossible dans les autres cases de la même région, soit qu'aucun autre nombre ne puisse apparaître dans les cases du groupe :
- si seuls les nombres du groupe peuvent apparaître dans les cases (mais la présence de ces nombres est éventuellement possible dans d'autres cases de la même région) : il s'agit alors d'un « groupe nu » ;
- si les nombres du groupe ne peuvent pas apparaître dans d'autres cases de la même région (mais d'autres nombres peuvent éventuellement apparaître dans les cases du groupe) : il s'agit alors d'un « groupe caché ».
On voit que ces définitions sont symétriques : si un groupe de n cases vides dans une région forme un groupe nu avec n candidats, les autres cases vides formeront un groupe caché (avec un nombre éventuellement différent de membres) avec le reste des candidats ; et inversement.
La recherche des singletons cachés a déjà été faite avec le balayage élémentaire, et les singletons nus ont déjà été identifiés avec la recherche des manquants et le marquage des paires. De même, les paires nues couplées peuvent être identifiées par un simple marquage des paires. Ces groupes nus et cachés non triviaux ne peuvent apporter du nouveau que dans les régions ayant de nombreuses cases libres : au minimum, si dans une même région il y a à la fois un groupe nu (de deux cases ou plus) et un groupe caché (de deux cases ou plus), la région a nécessairement au moins quatre cases libres ou plus. Si une région a moins de quatre cases libres, elle ne peut plus être réduite ; si un sous-groupe a moins de quatre membres, il ne peut pas lui-même être réduit ; et une fois qu'une telle région a été réduite, il n'est plus nécessaire de l'examiner par la suite.
La méthode ne trouve sa pleine application qu'à partir de cinq cases libres et la recherche de triplets nus : une région de cinq cases libres peut comporter un triplet nu (et une paire cachée), une région de six cases peut comporter un triplet ou un quadruplet nu (et, respectivement, un triplet ou une paire cachée), et ainsi de suite.
Quel que soit le groupe identifié, on peut alors éliminer les candidats:
- si le groupe identifié est nu, on peut le « cacher », en supprimant ses candidats des autres cases de la région ;
- s'il est caché, on peut le « dénuder », en supprimant du groupes les candidats qui n'en font pas partie.
Après cette réduction, la situation est celle d'une exclusion mutuelle : les nombres du groupe n'apparaissent pas ailleurs, et il n'y a que les nombres du groupe dans les cases.
Groupes nus

Le traitement des « paires liées » a été décrit avec le marquage des paires, et la possibilité d'identifier parfois quelques « triplets nus » y avait été signalée. Les « groupes nus » sont le cas plus général de ce traitement. Le raisonnement est le même que le groupe soit de deux, de trois, ou de quatre cases (et sera donné ici pour trois cases) ; mais il demande en pratique de marquer les candidats.
La règle est la suivante. Si dans une même région (ligne, colonne ou bloc), on observe un groupe de trois cases pour lesquelles :
i) il y a au plus trois candidats, et
ii) tous ces candidats sont pris parmi les trois mêmes valeurs ;
alors nécessairement, ces trois valeurs devront être prises sur ces trois cases, et ne peuvent pas aller ailleurs dans cette région.
La démonstration se fait par l'absurde : si l'une de ces trois valeurs candidates était affectée à une case autre de cette région, alors il ne resterait plus que deux valeurs possibles pour remplir ces trois cases, conduisant à une impossibilité.
De ce fait, quand cette configuration de groupe est identifiée, les valeurs du groupe ne peuvent pas être prises par les cases qui n'appartiennent pas au groupe : dans le reste de la région, les candidats correspondants à ces valeurs peuvent être supprimés.
Lorsque n est supérieur à 2, il arrive fréquemment qu'au moins une des cases du groupe n'ait pas comme candidats l'ensemble des chiffres de la liste : on parle alors de groupe « incomplet », mais cela n'enlève rien à la validité de la manœuvre d'élimination.
Les groupes nus exploitables par cette méthode comprennent deux, trois ou quatre éléments. On peut remarquer en effet que le cas limite d'un « groupe nu » à un élément correspond au cas des singletons nus. Inversement, si un « groupe nu » a plus que quatre éléments, on constate qu'en pratique, il est associé symétriquement à un « groupe caché » de moins de cinq éléments, qu'il est plus facile de rechercher.
De même que dans le cas des « singletons nus », ces configurations tirent leur nom de ce qu'elles sont immédiatement apparentes (dévoilées, donc « nues ») sur les grilles où les candidats ont été marqués. En effet, ces « groupes nus » peuvent facilement être recherchés formellement sur une grille où les candidats ont été marqués, et où ces triplets ont ainsi été rendus plus visibles : dès qu'une case n'a qu'un faible nombre de candidats, on recherche la possibilité d'un tel groupe, en regardant si d'autres cases de la même région (ligne, colonne ou bloc) ont des contraintes similaires.
Recherche des « groupes nus »
La recherche des « groupes nus » se fait après marquage des candidats, par balayage systématique des cases contenant deux, trois ou quatre candidats. Les étapes en sont typiquement, par ordre de difficulté croissante :
- Sur une case à deux candidats, on recherche sur les trois régions associées (ligne, colonne ou bloc) si une autre case contient les deux mêmes candidats.
- À défaut, sur une case à deux candidats, on recherche s'il existe dans la région deux autres cases ayant deux candidats dont un commun, ouvrant la possibilité d'un triplet lié incomplet (voire d'un quadruplet lié incomplet).
Ces deux premiers balayages peuvent être effectués même lorsque seules les paires candidates sont marquées.
Si ce premier balayage a échoué, un « groupe nu » aura nécessairement au moins trois candidats, dont au moins une case complète (sinon le groupe aurait été détecté dans l'étape précédente). Il formera donc formera un triplet ou un quadruplet :
- Sur une case à trois candidats, on recherche de même sur les trois régions associées si deux autres cases (y compris, le cas échéant, celles n'ayant que deux candidats) prennent leurs candidats dans ces trois mêmes valeurs.
- À défaut, on recherche s'il existe des cases de trois candidats dont deux communs, ouvrant la possibilité d'un quadruplet lié incomplet.
Si ce second balayage a échoué, un éventuel « groupe nu » aura nécessairement quatre candidat, dont au moins une case complète. En dernier ressort, on peut rechercher sur toutes les cases à quatre candidats si ces quatre mêmes candidats se retrouvent sur quatre cases différentes de la même région.
Groupes cachés

Une première remarque est que le complémentaire d'un groupe caché est un groupe nu : si sur les n+c cases libres, un sous-ensemble de c cases forment un « groupe caché » de c candidats (c'est-à-dire que ces c candidats n'apparaissent pas dans les n autres cases), le reste des n cases forme de son côté un groupe nu de n candidats (c'est-à-dire que les candidats du groupe c n'y figurent pas).
Pour rechercher un groupe caché, il faut chercher un groupe de c valeurs dont les candidats n'apparaissent que sur c cases d'une même région. Au sein de cet ensemble de cases, certaines ne contiennent pas le groupe au complet et peuvent contenir d'autres candidats étrangers au groupe. Alternativement, on peut chercher ce même groupe de c valeurs, qui soient exclues de n cases libres du groupe.
Le marquage ne permet pas de les identifier rapidement, et une recherche systématique est nécessaire, ce qui est à l'origine de la désignation de « groupe caché » : leur identification est beaucoup plus laborieuse que celle des « groupes nus », et conduit à des sudoku de difficulté plus importante. Il faut noter de plus que la difficulté croît très fortement avec le nombre de cases du groupe.
L'identification des groupes cachés peut souvent se faire indirectement par l'identification de groupes nus de taille supérieure. Dans l'exemple ci-contre, la recherche d'un triplet nu en colonne "f" conduit à remarquer le groupe "367" en Df et Ff.
- Il n'y a pas d'autre case en colonne "f" limitée aux candidats "367", mais le "3678" en Ef suggère d'étendre la recherche à des quadruplets nus.
- Il n'y a pas d'autre case en colonne "f" limitée aux candidats "3678", mais deux nouvelles cases y sont presque, en y ajoutant le candidat "9" : les cases Cf et Hf.
On a ainsi trouvé de proche en proche un groupe nu de cinq candidats "36789". Le complémentaire, correspondant aux cases Af, Gf et Jf, correspond dont à un groupe caché de trois valeurs "124".
La recherche directe d'un groupe caché porte sur des petits groupes de deux à trois candidats (exceptionnellement quatre), donc ne peut pas porter sur des candidats apparaissant plus souvent dans la région considérée. La recherche consiste à déterminer d'abord les candidats susceptibles de former un groupe caché dans la région, puis de vérifier sur les candidats identifiés s'ils forment effectivement un tel groupe. Pour reprendre l'exemple ci-contre :
- La recherche directe d'un triplet caché en colonne "f" conduit à limiter les membres potentiels aux candidats "1" (deux apparitions), "2", "4" et "9" (trois apparitions). Un triplet caché ne peut donc porter que sur les candidats "1249", l'un d'entre eux étant de trop.
- Un candidat apparaissant trois fois apparaîtra dans les trois cases du triplet caché. Le candidat "9" apparaissant deux fois sans le reste du groupe, il n'est pas possible qu'il fasse partie d'un triplet caché sur cette base, puisqu'il faudrait qu'un autre candidat du triplet fasse toutes ses apparitions sur une dernière case unique.
- Les candidats à tester se limitent donc à "124", et une vérification rapide montre qu'ils forment effectivement un triplet caché.
Fish ou Poissons (X-Wing, Swordfish, Jellyfish)

Pour rechercher ces configurations, on regarde si un candidat n'apparaît que dans un nombre précis de lignes et colonnes, pour lesquelles le nombre d'intersections est déterminé.
Le raisonnement qui permet l'élimination de candidats est le suivant dans le cas du X-Wing. Soient quatre cases a, b, c, d (exemple : Fa, Fj, Jj, Ja) contenant toutes un candidat K commun et formant un rectangle. Si sur les deux lignes (ab) et (cd), le candidat ne peut être présent qu'en a ou b, et en c ou d, alors on peut représenter le X-Wing par le rectangle abcd, ou par ses diagonales (ac) et (bd) qui forment un X. Dans cette situation, l'ensemble des possibilités se résument à deux cas. Dans le premier cas, K se trouve en a, donc il ne peut être ni en b, ni en d, ni sur la colonne de a. Comme K ne peut être en d, il se trouve nécessairement aussi en c, et ne peut donc pas apparaître dans la colonne de c. Dans le deuxième cas, K se trouve en b, donc il ne peut être en a, ni en c, ni dans la colonne de b. Donc K se trouve nécessairement aussi en d et ne peut apparaître dans la colonne de d. Dans les deux cas, sans savoir ou sera K, on voit qu'il ne peut apparaître ni dans la colonne de a, ni dans la colonne de b (sauf en a, b, c ou d), ce qui nous permet d'éliminer des candidats. Un raisonnement similaire peut être mené dans le cas symétrique où ce sont les lignes qui ne peuvent accueillir le candidat.
Le cas du Swordfish fait apparaître une figure non pas de 4 sommets comme le X-Wing, mais de six sommets. On peut le voir comme deux rectangles rattachés par un sommet. Ce sommet en commun n'a aucune utilité dans la figure, si bien qu'il ne reste que six sommets. Techniquement, il faut trouver 3 lignes (ou colonnes) où un candidat K n'apparaît qu'en deux cases. Ces cases étant alignées d'une ligne à l'autre deux à deux.
Une fois identifié, le traitement formel de ces groupes « marinés » est :
- X-Wing en ligne : si sur deux lignes, un candidat n’apparaît que sur les deux mêmes colonnes, alors on supprime ce candidat sur les deux colonnes sauf sur les deux lignes. Pour le X-Wing en colonne, on effectue le traitement en ligne.
- Swordfish : si sur trois lignes différentes, un candidat n’apparaît que sur trois colonnes, alors on supprime ce candidat sur les trois colonnes sauf sur les trois lignes.
Nota bene : il n’existe pas de règle homologue pour les blocs.
Symétries généralisées et tableau de résolution étendu
Dans The Hidden Logic of Sudoku[24], basé sur une formalisation logique systématique du jeu, toutes ses symétries généralisées ont été explicitées, en particulier entre les lignes et les nombres, entre les colonnes et les nombres et entre les blocs et les nombres. Une nouvelle méthode de résolution a été développée, basée sur leur exploitation systématique. Les espaces rn, cn et bn (complémentaires de l’espace usuel rc) ont ainsi été introduits (p. 35 de la première édition). Une grille de résolution étendue a été conçue, qui fait apparaître les liens de conjugaison comme des cases (de l’espace rc, rn, cn ou bn) à deux candidats et peut faciliter l’application de la méthode. De la sorte, les sous-ensembles cachés, ainsi que les X-wings, Swordfish et Jellyfish, apparaissent tous comme de simples Paires, Triplets ou Quadruplets. Dans un cadre général pour traiter des chaînes, ces symétries ont été utilisées pour introduire de nouvelles règles de résolution, comme les chaînes xy cachées et ultérieurement les chaînes nrczt. Cette méthode a été mise en œuvre dans un résolveur, SudoRules, basé sur des techniques d’intelligence artificielle et simulant un joueur humain.
Figures plus complexes : chaînes
Quand les techniques d’élimination de candidats basées sur des figures (ou patterns) simples ne suffisent pas, il faut recourir à des figures plus complexes, par exemple les chaînes. Une chaîne simple est une suite de candidats tels que chacun est lié au précédent. On peut définir plusieurs types de chaînes, qui peuvent tous être considérés comme des généralisations d’un unique type de base, la chaîne xy.
Chaînes xy
Une chaîne xy, est une suite de cases comportant uniquement des doublons, soit 2 candidats exactement. De plus ces cases doivent avoir un lien entre elles : on doit pouvoir passer de l'une à l'autre en restant dans une même région, tout en suivant « le fil » d'un candidat. Par exemple, pour une suite de quatre cases « bien disposées », on pourrait avoir les candidats suivants {1,9} {1,3} {3,6} {2,6}.
Dans les cas intéressants de chaînes, deux approches permettent l'élimination de candidats :
- Chaînes de type {a, b} {b, c} {c, d} {d, a}
Dans ce cas, on montre que pour toute case X, hors de la chaîne, contenant le candidat « a », et située à la fois dans la même région que la première case et dans la même région que la dernière case, alors cette case ne peut contenir le candidat « a ». Si « a » était vrai dans cette case, alors « a » serait faux dans la première case de la chaîne, et la chaîne se réduirait à {b} {c} {d} {a}. Or « a » ne peut être à la fois dans X et dans la dernière case de la chaîne. Donc X ne peut contenir « a ».
- Cas général : chaînes forcées
Partant d'une case A contenant {x, y} et que l'on voit deux « chemins » différents reposant sur des chaînes du type {x, y}{y, z}{z, t}{t, u}… arrivant à une case B contenant {t, u}, alors il se peut qu’indifféremment du choix de x ou de y dans la première case, et donc du chemin que l'on suit pour éliminer des candidats, un candidat soit systématiquement éliminé. Alors on vient de trouver une solution dans une case. Par exemple si le t de la dernière case est éliminé dans le cas où on choisit y en première case et qu'on suit le chemin 1 : {x, y}{y, z}{z, t}{t, u}, mais aussi dans le cas où on choisit x et qu'on suit le chemin 2 : {x, y}{x, v}{v, u}{u, w}{w, y}{y, t}{t, u}, alors u est la solution de la case B.
Ces raisonnements sont communs à tous les types de chaînes.
Généralisations des chaînes xy : chaînes d'ALS et chaînes nrczt
Parmi les généralisations logiques « naturelles » des chaînes xy, on a :
- les chaînes d’ALS (Almost Locked Sets), les plus anciennes et de loin les plus utilisées par les joueurs sur les forums de Sudoku ; un maillon de ces chaînes n’est plus un candidat mais un ALS (Almost Locked Sets), c’est-à-dire un ensemble de k cellules (sur une même ligne, une même colonne ou dans un même bloc) dont les candidats appartiennent à un ensemble de k+1 nombres ;
- les chaînes xyt, xyz et xyzt ainsi que leurs homologues « cachés » dans les espaces rn, cn et bn (définies dans la première édition de The Hidden Logic of Sudoku) ; les chaînes nrczt, ou chaînes supersymétriques, qui généralisent les précédentes en combinant toutes les cellules des espaces rc, rn, cn et bn (définies dans la seconde édition de The Hidden Logic of Sudoku[24])) ;
- une combinaison des deux, dont on peut trouver de nombreux exemples sur le forum sudoku-factory.
Règles résultant de l'hypothèse d'unicité
On exige en général d’un problème, qu’on dit alors bien formé, qu’il ait une solution et une seule. De toute évidence, cette exigence concerne d’abord le créateur de problèmes.
L’exigence qu’il y ait une solution ne pose pas de problème pour le joueur. Si elle n’est pas satisfaite par le créateur, le joueur pourra en général montrer la contradiction. Les règles mentionnées ci-dessus doivent en réalité s’interpréter de manière un peu plus subtile que sous la forme (usuelle) où elles ont été énoncées. La véritable interprétation est : « s’il y a une solution et si le candidat C est vrai, alors on a une contradiction ». D’où l’on conclut « s’il y a une solution, alors C est faux », et on élimine C des candidats. De cette manière, si le problème est contradictoire, on est certain qu’on ne trouvera pas de solution.
L’exigence d’unicité est plus délicate. Elle s’impose au créateur, mais le joueur ne peut d’aucune façon la contrôler. En pratique, cela signifie que, si un problème qui a plusieurs solutions est proposé mais que le joueur applique des règles découlant de l’hypothèse d’unicité, il peut faire ainsi des éliminations non justifiées (et rater des solutions alternatives ou aboutir à une situation où il croit qu’il n’y a pas de solution). Ce problème tend à disparaître en pratique car les créateurs de problèmes vérifient désormais plus sérieusement l’unicité.
Le principe du rectangle interdit
Considérons quatre cellules formant un rectangle s’étalant sur deux lignes, deux colonnes et seulement deux blocs. Si le contenu de ces quatre cellules est :
ab ab
ab ab
alors pour toute solution du problème ayant les valeurs
a b
b a
pour les cellules de ce rectangle, il existe une autre solution ayant les valeurs
b a
a b
et le problème ne peut donc avoir une solution unique.
La configuration initiale s’appelle rectangle interdit. À partir de là, on peut définir plusieurs règles visant à empêcher que cette situation se produise. Ces règles ne sont valables que sous l’hypothèse d’unicité.
Exemples de règle reposant sur l'exploitation du rectangle interdit
Règle UR1 : dans la configuration (où les quatre cellules forment un rectangle s’étalant sur deux lignes, deux colonnes et seulement deux blocs) :
ab ab
ab abc
éliminer a et b de la dernière cellule.
Règle UR2-H : dans la configuration (où les quatre cellules forment un rectangle s’étalant sur deux lignes, deux colonnes et seulement deux blocs) :
ab abc
ab abc
où les deux cellules de droite sont dans le même bloc, éliminer c de toute autre cellule liée aux deux cellules de droite.
Il existe de nombreuses variantes de ces règles.
Classification des problèmes
Il n’existe pas de classification universelle des différents problèmes : toute classification repose sur le choix d’un ensemble de méthodes de résolution. On peut cependant distinguer les classifications à large couverture (SER, SXT, NRCZT, etc.) et les classifications en quatre ou cinq niveaux (de « simple » à « diabolique »), comme ceux qui sont publiés dans les journaux. Ces dernières ne couvrent en général que des problèmes relativement simples, de SER ne dépassant pas 5 ou 6.
Il faut noter que chaque classification n’a de valeur qu’indicative et que, pour un joueur, deux problèmes ayant la même valeur dans une classification peuvent présenter des difficultés très différentes.
Préambule sur les problèmes minimaux et les statistiques de classification des puzzles
Une notion générale très utile d’un point de vue théorique est celle de problème minimal. Un problème est dit minimal (ou, plus rarement, « localement minimal ») s’il a une solution unique et si, chaque fois qu’on essaie de lui ôter un dévoilé, le puzzle obtenu (qui a toujours évidemment au moins une solution) se retrouve avoir plusieurs solutions.
Quand on veut faire des statistiques sur la classification des problèmes, il faut toujours se référer à des ensembles de puzzles minimaux, faute de quoi ces statistiques n’ont pas grand sens : en effet, en ajoutant autant de dévoilés qu’on veut, choisis parmi ses valeurs solutions, à un puzzle minimal, on peut obtenir de très nombreux puzzles qui auront évidemment la même solution, la plupart étant triviaux à résoudre.
À noter qu’il est très facile et rapide de créer par ordinateur des ensembles aléatoires de milliers de problèmes minimaux (avec, par exemple, le logiciel libre suexg (pour plus de détails sur la création de puzzles, voir plus loin).
La minimalité est une exigence annexe parfois attendue du créateur de problèmes. Elle est sans effet pour le joueur. Cependant elle peut être difficile à concilier avec d’autres exigences annexes, comme des exigences esthétiques, par exemple de symétrie, à savoir que les dévoilés se situent dans un ensemble de cellules présentant une certaine forme de symétrie. Il est plus difficile de créer des problèmes qui à la fois soient minimaux et aient certaines symétries (en particulier, suexg ne le fait pas).
Au cours de l'année 2008, il est apparu que les générateurs classiques de problèmes minimaux, qu'ils soient « bottom-up » ou « top-down » (c'est-à-dire qu'ils partent d'une grille vide et la remplissent petit à petit ou qu'ils partent d'une grille complète et éliminent des indices un par un) étaient tous fortement biaisés en faveur de problèmes avec peu d'indices. Une nouvelle sorte de générateurs a été introduite : les générateurs à biais contrôlé. Eux aussi sont biaisés mais leur biais est connu et peut donc être corrigé. Voir l'un des deux livres Constraint Resolution Theories[38], Pattern-Based Constraint Satisfaction and Logic Puzzles[39] ou l'article disponible sur le site de son auteur Unbiased Statistics of a CSP - A Controlled-Bias Generator[40].
SER (Sudoku Explainer Rating)
Le SER (Sudoku Explainer Rating) est de loin la classification la plus utilisée. Sudoku Explainer est un logiciel libre (en java), développé par Nicolas Juillerat et téléchargeable sur le web. Il peut être utilisé pour résoudre des problèmes mais aussi pour produire une estimation de leur difficulté, nommée leur SER. Celui-ci prend des valeurs de 1 à 11,7 (valeur maximale connue à ce jour).
Les règles qu’il utilise (dont certaines reposent sur l’hypothèse d’unicité) sont passablement hétérogènes et les valeurs affectées passablement ad hoc. À titre d’illustration, voici les niveaux associées à quelques-unes des règles définies plus haut.
- 1.0 à 2.3 Divers singletons
- 3.0 Paires Nues
- 3.4 Paires Cachées
- 3.6 Triplets Nus
- 3.8 Swordfish
- 4.0 Triplets Cachés
- 5.0 Quadruplets Nus
- 5.2 Jellyfish
- 5.4 Quadruplets Cachés
Les niveaux supérieurs font appel à divers types de chaînes :
- 11.6 Dynamic + Dynamic Forcing Chains (145-192 nodes) Cell Forcing Chains
- 11.7 Dynamic + Dynamic Forcing Chains (193-288 nodes) Double Forcing Chains
Ces Dynamic Forcing Chains sont une forme d’essais et erreurs.
Pour l'essentiel, la classification des problèmes les plus difficiles repose sur le nombre d'inférences élémentaires nécessaires pour l'élimination la plus difficile dans le cadre d'une procédure d'essais et erreurs à deux niveaux maximum (c’est-à-dire autorisant de faire des hypothèses sur un maximum de deux candidats simultanément). Ici, inférence élémentaire signifie soit un singleton (nu ou caché), soit l'élimination d'un candidat en contradiction directe avec une ou deux valeur(s) connue(s) ou supposée(s) par essais et erreurs.
Classification NRCZT
Cette classification, définie dans The Hidden Logic of Sudoku[24], est basée sur la longueur maximale de la chaîne nrczt nécessaire pour résoudre un problème. Contrairement au SER, un seul type de règle (les chaînes nrczt de diverses longueurs) est ici utilisé et cette classification, purement logique, indépendante de l’hypothèse d’unicité et indépendante de toute implémentation, est compatible avec toutes les symétries du jeu.
Bien que reposant sur des règles qui sont donc fort différentes de celles à la base du SER, cette classification est étroitement corrélée à celui-ci : une étude faite sur 10 000 problèmes minimaux différents (obtenus avec le générateur pseudo-aléatoire suexg) donne un coefficient de corrélation de 0,89. Cela signifie que ces deux classifications saisissent effectivement un aspect important de ce qui fait la complexité d’un problème.
Statistiques de la classification nrczt
Les statistiques de la classification nrczt sont accessibles :
- dans trois livres : The Hidden Logic of Sudoku[24], Constraint Resolution Theories[38] et Pattern-Based Constraint Satisfaction and Logic Puzzles[39]
- et dans deux articles du même auteur : From Constraints to Resolution Rules, Part II: chains, braids, confluence and T&E[41] (sur la base de 10 000 problèmes minimaux aléatoires) et Unbiased Statistics of a CSP - A Controlled-Bias Generator[40].
Les résultats suivants sont basés sur le nouveau générateur à biais contrôlé (et sur Presque six millions de problèmes minimaux aléatoires); ils sont non biaisés. Ce générateur et la vaste collection associée sont accessibles sur la plateforme GitHub : https://github.com/denis-berthier/Controlled-bias_Sudoku_generator_and_collection
Le résolveur de Sudokus ayant servi à établir cette classification (SudoRules, partie du logiciel plus général de résolution de contraintes CSP-Rules) est accessible sur la plateforme GitHub : https://github.com/denis-berthier/CSP-Rules-V2.1
La répartition en pourcentage par niveaux nrczt se fait ainsi :
- niveau 0 : 29,17
- niveau 1 : 8,44
- niveau 2 : 12,61
- niveau 3 : 22,26
- niveau 4 : 21,39
- niveau 5 : 4,67
- niveau 6 : 1,07
- niveau 7 : 0,29
- niveau 8 : 0,072
- niveau 9 : 0,020
- niveau 10 : 0,005 5
- niveau 11 : 0,001 5
Sachant que la complexité effective d’un problème croît de manière quasi exponentielle avec son SER ou son NRCZT, ces chiffres montrent que :
- une très grande majorité des problèmes peut se résoudre par des techniques relativement simples (ici, des chaînes courtes) ;
- il reste malgré tout des problèmes de très grande complexité, ce qui justifie que les joueurs experts recherchent en permanence de nouvelles règles qui permettraient de simplifier les solutions obtenues avec les règles connues à ce jour ;
- les problèmes exceptionnellement complexes (comme le fameux Easter Monster[42]) ont très peu de chances d’être trouvés par un générateur aléatoire et certains joueurs essaient en permanence de créer de nouveaux exemples « à la main ».
Résultats collatéraux : la technique des générateurs à biais contrôlé permet aussi d'estimer le nombre de problèmes minimaux (3,10 × 1037) ainsi que le nombre de problèmes minimaux non équivalents (2,55 × 1025).
Classifications des problèmes « grand public »
La plupart des auteurs des manuels sur le sudoku sont d’accord sur le fait que plusieurs facteurs influent sur la difficulté de ces problèmes dont l’équation de base tient compte modulo une certaine pondération :
- du nombre de cellules à remplir ;
- du nombre de cellules remplies par élimination ;
- du nombre de groupes indépendants de multiples numériquement liés, traitables suivant une seule dimension ; région, ligne ou colonne ;
- du nombre de groupes indépendants de multiples numériquement liés, traitables suivant deux dimensions à la fois ; région × ligne, région × colonne ou colonne × ligne ;
- du nombre de groupes indépendants de multiples numériquement liés, traitables suivant les trois dimensions à la fois ; région × ligne × colonne ;
- du nombre d’hypothèses à faire en cas de blocage momentané ;
- du nombre d’itérations de l’heuristique de résolution ;
- du nombre de recherches à faire pour compléter la grille.
Cependant, cette question de difficulté fait toujours l’objet de nombreux débats dans les forums sur le sudoku, car elle est liée aux concepts et représentations visuelles que chacun est prêt à adopter. Mais elle peut être complètement élucidée si l'on hiérarchise, du simple au complexe, les techniques et procédés que l'on peut utiliser pour réussir une grille, et si l'on considère notre manière de jouer (observer certaines règles de handicap, comme la résolution intégrale par raisonnement mental uniquement, ou l'interdiction absolue de reproduire la grille-problème en plusieurs grilles en faisant des hypothèses, etc.).
Mais, il ne faut pas confondre le niveau du joueur avec le degré de difficulté d’une grille. Certains joueurs sont capables de réussir une grille en raisonnant mentalement, sans écrire de multiples dans les cases qui ne reçoivent par la suite, chacune, que le bon chiffre, alors que d’autres peinent avec des cases présentant plusieurs candidats, ou avec plusieurs grilles provenant des hypothèses gratuitement émises, ou élaborées selon les catégories (lignes, colonnes et régions) dont la grille-conjointe par exemple, qui englobe en fait un certain tableau étendu de résolution. C’est pourquoi on préfère classer les grilles-problèmes en cinq types, au sein desquels on retrouve différents niveaux de difficulté :
Type 1
Utilisation des techniques simples dont « la recherche de la bonne case pour un chiffre et une région donnés » par réduction par croix, et « la recherche, du bon chiffre pour une cellule donnée », par décompte, bien que cette dernière soit un peu plus fastidieuse que la première. En principe, pour ce type de grilles, le raisonnement se fait mentalement, sans que l’on soit obligé d’inscrire les candidats éventuels dans une cellule donnée, et le remplissage de la grille se fait progressivement en suivant l’une des innombrables pistes ou enchaînements qui se présentent. C’est ce type de grilles que vous trouvez fréquemment dans les sites, journaux et magazines ou créées par des logiciels, classant à tort certaines d’entre elles, dans la catégorie des « difficiles » ou même « diaboliques » ! La raison en est qu’il existe une classe de grilles de type 1, vraiment difficile à réussir par calcul mental. Et donc, ne sous-estimez pas les grilles de type 1 : il y en a des « faciles », « moyennes » et même « difficiles ».
Type 2
Utilisation des techniques permettant le traitement des cellules-à-candidats-multiples selon une seule dimension ; ligne, colonne ou région, dont « l’élimination à cause des paires nues », « le dégraissage des candidats cachés » et « le dégraissage des paires camouflées ». Certaines grilles de type 2 peuvent être réussies, comme pour le type 1, mentalement. D’autres, d’un niveau supérieur, nécessitent que l’on inscrive, au fur et à mesure, les candidats dans les cellules d’une région, une ligne ou une colonne, sans toutefois le faire pour toutes les cellules vides, et voir si l’on peut simplifier les multiples par l’une des trois techniques précédentes. Les plus difficiles des grilles de ce type 2 ne se prêtent à la résolution qu’une fois que toutes les cellules contiennent leurs candidats probables. Dans ce cas, il faut essayer d’arriver à la situation optimale de la grille : dans chaque catégorie (ligne, colonne et région), les groupes des « multiples numériquement liés » doivent être « indépendants». D’autres techniques simples de traitement selon une seule dimension peuvent être utilisées, dont « l’élimination à cause des triplets nus » et « le dégraissage des triplets camouflés ». Cette dernière est plus pénible à faire ! On pourra également éliminer certains chiffres par une technique simple de traitement, cette fois-ci, à deux dimensions ligne × région ou colonne × région : « la répartition d’un bloc en quatre domaines complémentaires ou alternés ». Donc, si vous optez pour un exercice mental, ce type de grilles vous propose de bien difficiles. Et si vous vous permettez d’inscrire les multiples dans les cellules, vous avez là de très beaux exercices d’entraînement sur la stratégie de traitement des « groupes indépendants de multiples numériquement liés ».
Type 3
Utilisation des techniques permettant la simplification des cellules-à-candidats-multiples, d’abord comme pour le type 2, selon une seule dimension ; ligne, colonne ou région, mais avec une taille plus grande dont « l’élimination à cause des quadruplets et quintuples nus » et «le dégraissage des quadruplets et quintuples cachés ». Procéder par cette dernière technique, qui est d’ailleurs plus fastidieuse à mener, c’est en fait utiliser « l’élimination à cause d’un ou de deux groupes nus » mais de taille inférieure !
Certaines grilles de type 3 nécessitent un traitement selon deux dimensions (lignes × colonnes, lignes × régions et/ou colonnes × régions) en utilisant des procédés beaucoup plus astucieux, mais justifiables dont X-Wing, Swordfish, Jellyfish, Squirmbag ou la TPU, la technique découlant du « principe de l’unicité de la solution ». Donc pour ce type de grilles, il ne faut pas espérer aboutir à la solution rien qu’en raisonnant mentalement, sans avoir dorénavant mis tous les candidats possibles dans toutes les cellules. Trois degrés de difficulté sont possibles, selon la taille des groupes nus ou camouflés, mais aussi selon leur nombre.
Type 4
La stratégie adoptée pour les grilles de ce type, présentant des cas de figures plus complexes, consiste à prendre en considération simultanément les trois dimensions (lignes × colonnes × régions). Il faut donc pouvoir « sauter » d’une région à une autre, à travers les cases, en utilisant des « passerelles » matérialisées soit par une ligne, une colonne ou une région. Bref, il faut se créer des « chemins » entre les différentes cases. Ainsi, on reconnaîtra des procédés similaires à ceux déjà utilisés par traitement à deux dimensions dont le X-Wing par exemple (les sommets ne sont plus ceux d’un rectangle, mais parmi ceux d’un polygone). Précisons que cette stratégie est basée sur la logique bivalente (pour un chiffre N fixé et une case donnée de multiples, p : « N est la valeur » ou non(p) : « N n’est pas la valeur »).
Vu d’un certain angle, il s’agit de superposer deux ou plusieurs grilles sur la même grille-problème initiale, de faire une conjugaison logique des différentes propositions (concrétisées par des chemins) et de déterminer celles des grilles qui aboutissent à une contradiction avec l’une des règles qui régissent le jeu sudoku, pour découvrir la bonne solution. C’est donc comme si l’on procède par formulation par hypothèse, mais d’une manière détournée ! Il faut avouer que cette manière de faire procure plus de plaisir à jouer et à appliquer des procédés que d’émettre des hypothèses pour obtenir des grilles « pauvres » au niveau intellectuel ! Utilisez des crayons de couleur. Ceux qui sont déjà initiés à cette technique reconnaîtront des grilles faciles, moyennes et même difficiles.
Type 5
Certains journaux, magazines, sites et logiciels livrent des grilles dites «diaboliques» voire «infernales». Le plus souvent, ces grilles peuvent être résolues par les techniques mises au point jusqu’à ce jour, et sont beaucoup moins difficiles qu'il n'y parait. En effet, une grille diabolique est celle qui ne peut être résolue par aucun des procédés mis au point jusqu’à ce jour, sauf par la formulation d’une ou de plusieurs hypothèses sur les chiffres à mettre dans une ou plusieurs cases. Bien entendu, l’unicité de la solution pour la grille est requise.
Désormais, c’est le seul moyen pour aboutir à la solution, en attendant l’élaboration de nouveaux procédés « manuels ».
Signalons enfin, qu’au niveau de la construction des grilles-problèmes, il est fréquemment plus facile d’obtenir une grille de type 1, et presque rare de tomber sur une grille de type 4 ou 5. Les logiciels élaborés jusqu’à ce jour partent bien sûr des différents procédés de résolution, pour fabriquer un problème, mais le niveau souhaité baisse généralement d’un ou même de deux degrés. Statistiquement, on relève que la distribution de la fréquence par type tourne autour de 46 %, 32 %, 11 %, 8 % et 3 %, du premier type au cinquième.
Informatique et Sudoku
Solutions logicielles
Pour un informaticien, programmer la recherche d’une solution par le biais des contingences ou de multiples contingences (tel qu’exigé pour les problèmes les plus difficiles) est une tâche relativement simple. Un tel programme imite un joueur humain qui recherche une solution sans recourir au hasard.
Il est aussi relativement simple de concevoir un algorithme de recherche par backtracking. De façon habituelle, il suffit à l’algorithme de choisir 1 pour la première cellule, puis 2 pour la prochaine, ainsi de suite tant qu’aucune contradiction n’apparaît. Lorsqu’une contradiction apparaît, l’algorithme essaie une autre valeur pour la cellule qui amène la contradiction. Une fois toutes les possibilités épuisées pour cette cellule, l’algorithme « revient sur ses pas » et recommence avec l’avant-dernière cellule.
Bien que cet algorithme ne soit pas très élégant, il est certain de trouver une solution s’il en existe. Une grille 9×9 est habituellement résolue en moins de trois secondes avec un ordinateur personnel moderne qui a recours à un interpréteur, et en quelques millisecondes avec un langage compilé. Cependant, il existe des grilles qui sont particulièrement difficiles à résoudre par backtracking (voir (en) Algorithmics of Sudoku#Brute-force algorithm).
Une mise en œuvre particulière du backtracking est de recourir à la programmation logique, telle qu’implantée dans Prolog. Dans ce cas, le concepteur fournit au programme les contraintes de la grille (un chiffre par rangée, par colonne et par région ; les chiffres dévoilés) ; ce programme prendra les décisions pour résoudre le problème. Si l’on admet que la grille a une solution unique, la recherche est certaine d’aboutir.
Donald Knuth a mis au point un algorithme qui fait appel aux listes doublement chaînées (les dancing links[43]), et qui se révèle très efficace pour résoudre ce type de sudokus en quelques millisecondes.
Une autre solution, proposée en 2007 par le chercheur en méthodes formelles Nicolas Rapin, consiste à utiliser la structure de diagramme de décision binaire (BDD en abrégé) pour résoudre et représenter au sein d'une structure unique l'espace des solutions d'une grille. L'idée consiste à modéliser la présence du chiffre k en ligne i, colonne j, par la variable booléenne nommée x_i_j_k en prenant pour convention que la valeur vrai de cette variable représente la présence du chiffre k en ligne i, colonne j et la valeur faux son absence. Il faut donc 9×9×9 variables booléennes pour modéliser une grille de sudoku 9×9. Les contraintes inhérentes au sudoku peuvent alors être écrites directement sous la forme de formules booléennes et passées à une bibliothèque de BDD. Cette approche présente l'avantage de pouvoir résoudre non seulement des grilles de sudoku bien formées (ayant une seule solution) mais aussi d'énumérer toutes les solutions de grilles mal formées ayant plusieurs solutions (les solutions étant données par les chemins du diagramme menant à la feuille 1) ou encore de prouver qu'une grille mal formée ne présente aucune solution. Cette méthode peut donc être utile pour la résolution, l'élaboration et la validation de grilles. En posant que → dénote l'implication logique, ! la négation et V la disjonction, voici un exemple de contrainte de région : x_1_1_1 → ! (x_1_2_1 V x_1_3_1 V x_2_1_1 V x_2_2_1 V x_2_3_1 V x_3_1_1 V x_3_2_1 V x_3_3_1). En langage naturel cette expression signifie : si le chiffre 1 est présent en ligne 1, colonne 1, alors il n'est pas présent ailleurs dans sa région. Les contraintes de colonne sont de la forme x_i_j_k → ! ( x_h_j_k), celles de ligne de la forme x_i_j_k → ! ( x_i_h_k) et celle de présence d'un chiffre pour toute case i,j de la forme x_i_j_h. Pour les cases remplies de la grille, les contraintes implicatives ci-dessus (région, ligne, colonne) se réduisent au conséquent (terme à droite de l'implication) puisque l'antécédent est vrai. Lors de la mise en œuvre de cette solution, on observe que l'efficacité générale est très sensible à l'ordre dans lequel les contraintes sont passées à la bibliothèque de construction du BDD. Sur un PC standard (1,6 GHz, 1 Gio de RAM) la durée de résolution de grilles bien formées se situe entre 1 s et 2 min 30 s (selon les grilles). Des implémentations libres sont disponibles[44].
Il existe aussi de nombreux programmes librement disponibles sur le web, basés sur l’implémentation de règles utilisées par les joueurs : Sudocue, Sudoku Explainer, Sudoku Susser, Sudoktor, Sadman, le solveur de gsf. Le programme SudoRules, désormais public, est basé sur des techniques d’intelligence artificielle; il fait partie d'un logiciel plus général de résolution de problèmes de satisfaction de contraintes (qui inclut aussi d'autres jeux logiques). Il est disponible sur la plateforme GitHub : https://github.com/denis-berthier/CSP-Rules-V2.1.
Construction de grilles
Il semblerait que les grilles de Dell Magazines, le pionnier dans le domaine de la publication, soient créées par ordinateur. Elles sont habituellement composées de 30 chiffres dévoilés répartis au hasard. L’auteur des grilles est inconnu. Durant l’hiver 2000, Wei-Hwa Huang a affirmé qu’il était l’auteur du programme qui crée ces grilles ; selon lui, les grilles antérieures étaient construites à la main. Le générateur serait écrit en C++ et, bien qu’il offre certaines options pour satisfaire le marché japonais (symétrie et moins de chiffres), Dell préfère ne pas les utiliser. Certains spéculent que Dell continue à utiliser ce programme, mais aucune preuve ne soutient leur affirmation.
Les sudoku de Nikoli, important créateur de sudoku au Japon, sont construits à la main, le nom de l’auteur apparaissant avec chaque grille publiée ; les dévoilés sont toujours présentés de façon symétrique. Cet exploit est possible en connaissant à l’avance l’endroit où seront les dévoilés et en affectant par la suite un chiffre aux cellules ainsi choisies. Le Number Place Challenger de Dell affiche aussi le nom de l’auteur. Les grilles publiées dans la plupart des journaux britanniques seraient créées automatiquement, mais font appel à la symétrie, ce qui laisserait sous-entendre qu’un humain les crée. The Guardian affirme que ses grilles sont créées à la main par des Japonais, mais aucune mention de l’auteur n’est faite. Elles seraient construites par des gens de Nikoli. The Guardian a affirmé que puisqu’ils sont construits à la main, ils contiennent de « subtiles allusions » hautement improbables dans les grilles construites par ordinateur.
Il est possible de construire des grilles avec de multiples solutions ou sans solution, mais celles-ci ne sont pas considérées comme d’authentiques sudoku. Comme pour beaucoup d'autres jeux logiques, une solution unique est requise. Une grande attention est donc nécessaire lors de la construction d’une grille, puisqu’un seul chiffre mal placé risque de rendre la résolution de celle-ci impossible.
Le logiciel libre (suexg) permettant de construire des problèmes minimaux (plusieurs dizaines à la seconde) est disponible sur le Web.
La minimalité est une exigence annexe parfois attendue du créateur de problèmes, bien qu’elle soit sans effet pour le joueur. Elle peut être difficile à concilier avec d’autres exigences annexes, comme des exigences esthétiques, par exemple de symétrie, à savoir que les dévoilés se situent dans un ensemble de cellules présentant une certaine forme de symétrie. Il est plus difficile de créer des problèmes qui à la fois soient minimaux et aient certaines symétries (en particulier, suexg ne le fait pas).
Notes et références
- « メンテナンス情報 (Maintenance information) / J-PlatPat/AIPN », sur j-platpat.inpit.go.jp (consulté le ).
- « Sudoku Variations », sur Mathpuzzle (consulté le ).
- (en) Mark Swaney, Magic Squares.
- Problème VI « Problèmes plaisants et délectables qui se font par les nombres ».
- (de) Sudoku Anleitung.
- Jean Robin, « L'inventeur du sudoku est français », sur leparisien.fr, (consulté le ).
- http://www.time.com/time/magazine/article/0,9171,2137423,00.html
- « Japon : Le "père du Sudoku" est mort à 69 ans », sur BFMTV, (consulté le ).
- (fr) http://www.kuboku.com/
- (en) « http://www.knightfeatures.com/KFWeb/content/features/kffeatures/puzzlesandcrosswords/KF/Sudoko/sudoku_word.html »(Archive.org • Wikiwix • Archive.is • Google • Que faire ?) (consulté le ).
- (en) http://sudoku.top-notch.co.uk/wordoku.asp
- « Custom Sudoku »
- (en) http://www.mathrec.org/sudoku
- (en) http://sudoku.top-notch.co.uk/superwordoku.asp
- (en)Walter T. Federer. Experimental design: theory and application. Macmillan, New York, 1955, 544 + 47 p.
- Pierre Dagnelie. Avant le sudoku : le carré latin magique. Revue Modulad 39, 172-175, 2008 (ou [PDF]).
- Carrés magiques en Chine.
- (en) Origine retrouvée dans les journaux français dans les années 1890 jusque vers les années 1930, relevée dans un article britannique du Times daté du 3 juin 2006.
- (en) « http://www.mathsisfun.net/SingleNumber.sit »(Archive.org • Wikiwix • Archive.is • Google • Que faire ?) (consulté le ).
- (en) « http://www.mathsisfun.net/SingleNumber.prc »(Archive.org • Wikiwix • Archive.is • Google • Que faire ?) (consulté le ).
- (en) G2, home of the discerning Sudoku addict, The Guardian, publié le 13 mai 2005.
- (en) « The World’s Largest Sudoku Puzzle: Win £5000, Sky One, consulté le 28 mai 2009 »(Archive.org • Wikiwix • Archive.is • Google • Que faire ?) (consulté le ).
- (en) [PDF].
- (en) Denis Berthier, « The Hidden Logic of Sudoku », Lulu Publishers, (ISBN 978-1-84753-472-9, lire en ligne, consulté le ).
- (ja) http://www2.ic-net.or.jp/~takaken/auto/guest/bbs46.html
- (en) http://www.csse.uwa.edu.au/~gordon/sudokumin.php
- (en) Sudoku enumeration problems.
- suite A107739 de l'OEIS.
- Jean-Paul Delahaye, Le problème du Sudoku, Pour la science no 447, janvier 2015, p. 76-81
- (en) http://www.shef.ac.uk/~pm1afj/sudoku/sudgroup.html et suite A109741 de l'OEIS
- (ja) プログラミングパズル雑談コーナー.
- (en) Minimum Sudoku.
- (en) Gary McGuire : There is no 16-Clue Sudoku: Solving the Sudoku Minimum Number of Clues Problem[PDF].
- Pierre Barthélémy, « 17 est le nombre de Dieu au sudoku », sur lemonde.fr, (consulté le ).
- D'après (en)SadMan Software: Sudoku Solving Techniques - Naked Single / Singleton / Sole Candidate.
- D'après (en)SudoCue - Sudoku Solving Guide.
- (en) Denis Berthier, From Constraints to Resolution Rules, Part I: Conceptual Framework, International Joint Conferences on Computer, Information, Systems Sciences and Engineering (CISSE 08), December 5-13, 2008.
- (en) Denis Berthier, « Constraint Resolution Theories », Lulu Publishers, (ISBN 978-1-4478-6888-0, lire en ligne, consulté le ).
- (en) Denis Berthier, « Pattern-Based Constraint Satisfaction and Logic Puzzles », Lulu Publishers, (ISBN 978-1-291-20339-4, lire en ligne, consulté le ).
- Denis Berthier, Unbiased Statistics of a CSP - A Controlled-Bias Generator, International Joint Conferences on Computer, Information, Systems Sciences and Engineering (CISSE 09), 4-12 décembre 2009.
- Denis Berthier, From Constraints to Resolution Rules, Part II: chains, braids, confluence and T&E, International Joint Conferences on Computer, Information, Systems Sciences and Engineering (CISSE 08), 5-13 décembre 2008.
- Voir (en)Solution to the Easter Monster Puzzle: Formal Logic and Number Pair Chains ou (en)Easter Monster pour une étude de la solution du « easter monster ».
- (en) Knuth: Preprints.
- « robdd based sudoku solver »
Voir aussi
Bibliographie
- Narendra Jussien, Précis de Sudoku, Hermès Lavoisier, 2006, 188 pages (ISBN 2-7462-1559-4).
- (en) Denis Berthier, The Hidden Logic of Sudoku, Lulu Publishers ; 1re édition, , 384 pages (ISBN 978-1-84753-472-9) ; deuxième édition, , 416 pages (ISBN 978-1-84799-214-7).
- (en) Denis Berthier, Constraint Resolution Theories, Lulu Publishers, , 308 pages (ISBN 978-1-4478-6888-0).
- (en) Denis Berthier, Pattern-Based Constraint Satisfaction and Logic Puzzles, Lulu Publishers, , 484 pages (ISBN 978-1-291-20339-4).
- « Le tsunami du sudoku », Pour la science, no 338, , p. 144.
- (en) Denis Berthier, From Constraints to Resolution Rules, Part I: Conceptual Framework, International Joint Conferences on Computer, Information, Systems Sciences and Engineering (CISSE 08), December 5-13, 2008; re-publié comme chapitre du livre Advanced Techniques in Computing Sciences and Software Engineering, Springer, 2010 (OCLC 5662041121).
- (en) Denis Berthier, From Constraints to Resolution Rules, Part II: chains, braids, confluence and T&E, International Joint Conferences on Computer, Information, Systems Sciences and Engineering (CISSE 08), December 5-13, 2008; re-publié comme chapitre du livre Advanced Techniques in Computing Sciences and Software Engineering, Springer, 2010 (OCLC 5661887312).
- (en) Denis Berthier, Unbiased Statistics of a CSP - A Controlled-Bias Generator, International Joint Conferences on Computer, Information, Systems Sciences and Engineering (CISSE 09), December 4-12, 2009; re-publié comme chapitre du livre Innovations in Computing Sciences and Software Engineering, Springer, 2010 DOI 10.1007/978-90-481-3660-5_28.
Articles connexes
- Hors origine japonaise
- Nombres fléchés
- Carré latin
- Énigmes géométriques.
- Créateurs et éditeurs de jeux
Liens externes
- Ressource relative à la santé :
- (en) PatientLikeMe
- Notices dans des dictionnaires ou encyclopédies généralistes :
- À propos de la soudaine popularité du sudoku au Royaume-Uni :








![\vee _{{h\in [1,9]}}](https://img.franco.wiki/i/3abb7a8cca88af4f18ba3984af62ed456c6548b3.svg)