Chiffres arabes

Généalogie des numérations brahmi, gwalior, sanskrit-dévanagari et arabes (1935).

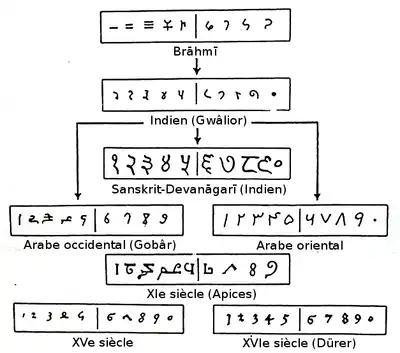
Les chiffres arabes tirent leur origine du système de numération indo-arabe, né en Inde.

La graphie originale des chiffres indiens pourrait s'inspirer d'une numération décimale non positionnelle indienne datant du III^e siècle av. J.-C., la numération Brahmi[2].

Un témoignage de leur utilisation en Inde est avéré en Syrie, au milieu du VII^e siècle, dans un commentaire de l'évêque Sévère Sebôkht sur les sciences grecques et les sciences orientales[3]. Ils sont repris par les mathématiques arabes et décrits dans un ouvrage du IX^e siècle du mathématicien persan Al-Khwârizmî sur la numération décimale positionnelle[4].

Les premiers chiffres arabes connus en Europe figurent dans le Codex Vigilanus de 976, Monastère de Saint Martin de Albeda, Royaume de Pampelune.

Au Maghreb (terme qui comprend à l'époque aussi la péninsule Ibérique sous domination musulmane), les chiffres arabes d'origine indienne prennent une forme particulière: ce sont les premiers chiffres arabes occidentaux. En arabe, cette graphie est appelée ghubar (autre translitération: ghobar), d'un mot signifiant "poussière". Ceci serait dû au fait que pour effectuer des calculs on traçait les chiffres dans le sable ou la poussière[5].

Les premiers documents connus qui contiennent ces signes datent des années 874 et 888[6].

D'après Georges Ifrah, cette forme particulière pourrait être une adaptation à l'écriture arabe maghrébine. (Cependant, on ne sait pas si ce style d'écriture s'était déjà répandu avant le X^e siècle.) Il pense également que la forme a été fixée par des vers mnémotechniques, attestés dans plusieurs manuscrits, qui font un lien avec des lettres de l'alphabet arabe[6].

Au X^e siècle, les chiffres arabes de l'époque gagnent la péninsule Ibérique, alors sous domination omeyyade. C'est leur première apparition en Europe, certes encore dans le monde arabo-musulman.

Les étiquettes utilisées sur les jetons des abaques, selon divers manuscrits médiévaux.

En Occident, les chiffres arabes apparurent une première fois dans le contexte de l'abaque.

Dans ce cadre, certains mettent l'accent sur les travaux de Gerbert d'Aurillac (940–1003), le futur pape Sylvestre II, qui étudia les mathématiques et l'astronomie à Vic en Catalogne et s'y initia aux sciences et techniques islamiques. A cette époque de sa vie, il entra probablement en contact avec les chiffres arabes, encore sans le zéro[7]. (Des légendes selon lesquelles il serait allé jusqu'à Cordoue, voire à l'Université Al Quaraouiyine de Fès au Maroc[8], sont sans fondement [9] - [10] - [11] - [12] - [13] - [14].)

En tout cas, Gerbert est entre autres à l'origine d'un type particulier d'abaque, l’abaque de Gerbert, où les jetons multiples sont remplacés par un jeton unique portant comme étiquette un symbole numérique: les sept jetons de la colonne unité sont remplacés par un jeton portant le numéro 7, les trois jetons de la colonne dizaine par un jeton portant le chiffre 3, etc. (Une telle étiquette s'appelle en latin apex, au pluriel apices.) Il est possible, mais douteux, que Gerbert ait utilisé les chiffres arabes pour ces étiquettes[15].

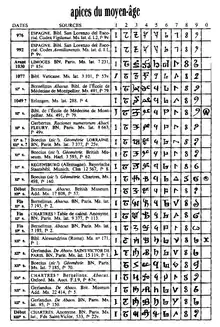
Quoi qu'il en soit, d'autres à partir du XI^e siècle ont utilisé l'abaque de Gerbert avec les chiffres arabes[16], comme en témoignent plusieurs manuscrits médiévaux (voir illustration).

Dans ces manuscrits, les graphies sont très diverses, et parfois assez éloignées de leur modèle arabe (occidental). Une première raison possible est l'adaptation à divers styles d'écriture régionaux de l'Occident médiéval. La seconde raison, plus importante: Dans certaines écoles, on prit l'habitude d'utiliser les jetons "à l'envers". (Après tout, il est facile de faire ce genre d'"erreur" avec un abaque, et cela ne change rien au fonctionnement des calculs.) C'est ainsi que de nombreuses graphies sont le résultat d'une rotation. Cela explique aussi que le chiffre six reçut à l'époque un tracé anguleux, pour éviter la confusion avec le neuf[17].

À côté de l'abaque, les chiffres arabes furent introduits une seconde fois avec la méthode des calculs écrits, qui ne nécessite pas d'abaque.

Cette fois, la forme des chiffres est plus proche de la graphie arabe occidentale, et différente de celles des abaques. Nos chiffres modernes proviennent de cette tradition[18].

Vers la fin du XI^e siècle, avec la Reconquista, les chrétiens reprennent aux musulmans des territoires. Ils gagnent ainsi accès à de nombreux manuscrits, notamment scientifiques. Tolède notamment est prise en 1085, et ses manuscrits attirent des intellectuels de toute l'Europe chrétienne. Par la suite, c'est surtout au XII^e siècle que de nombreux textes sont traduits de l'arabe au latin[19]. Parmi ces traductions, il nous reste quatre adaptations en latin du livre d'Al-Khwarizmi sur les chiffres indiens, dont le titre arabe est Kitab al-hisab al-hindi. Ces adaptations datent au moins en partie du XII^e siècle. Il n'y a pas de consensus sur les auteurs de ces textes[20].

Le nouveau système ne tarde pas à être appelé « algorisme » (du nom latinisé d'Al-Khwarizmi, Algorizmi, et modifié plus tard en algorithme), ses partisans « algoristes », et ses opposants « abacistes » (partisans de l'abaque)[21].

D'autres attribuent un rôle majeur au mathématicien Leonardo Fibonacci (environ 1170–1250), originaire de Pise en Italie actuelle. Il étudia auprès de professeurs musulmans à Béjaïa (dans l'actuelle Algérie) et ramena à Pise en 1198 une partie de leur savoir. Il publia, en 1202, le Liber abaci (Le livre du calcul), un traité sur les calculs et la comptabilité. Sa méthode est fondée sur le calcul décimal avec les "chiffres indiens" (c'est le nom qu'il utilise)[22].

Dame Arithmétique, arbitrant une compétition entre Boèce, utilisant l'écriture et les chiffres arabes, et Pythagore, utilisant l'abaque. Elle regarde en direction de Boèce, qui semble largement avoir sa faveur. Bien sûr, historiquement, Boèce n'a pas pu connaître les chiffres arabes.

Comme beaucoup de solutions qui nous paraissent simples, utiles et ingénieuses parce qu'elles nous sont familières, la diffusion des chiffres arabes s'est heurtée aux habitudes traditionnelles, et leur apprentissage a été progressif. À Florence (Italie), il fut d'abord interdit aux marchands de les employer dans les contrats et les documents officiels[23]. En 1299, ils sont partout interdits, y compris dans la comptabilité privée des banquiers et marchands florentins[24]. Tant que les opérations restent simples, l'abaque pour le calcul et les chiffres romains pour la représentation graphique suffisent. À partir de la Renaissance, avec le développement exponentiel du commerce, puis des sciences, en particulier de l'astronomie et de la balistique, la nécessité d'un système de calcul puissant et rapide s'impose : les chiffres indo-arabes écartent définitivement leurs prédécesseurs romains. Leur tracé définitif, normalisé, est attesté dès le XV^e siècle.

Le développement des chiffres décimaux dans l'Europe jusqu'au XVIII^e siècle est montré dans l'illustration ci-dessous de Jean-Étienne Montucla, qui fut publiée 1758 dans son Histoire de la mathématique :

Comparaison des notations. Pour des explications cliquez sur le document.

• Système de numération
• Système de numération indo-arabe
  • Numération indienne
  • Chiffres arabes orientaux
• Al-Khwârizmî
• Système décimal
• Nombres : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
• Nombres dans le monde
• Nombres en français

• Georges Ifrah, Histoire universelle des chiffres, Paris, Seghers, 1981, 568 p. (ISBN 2-221-50205-1), Chapitre 30: L'origine des chiffres "arabes" (p. 453-518).