Vérification de modèles
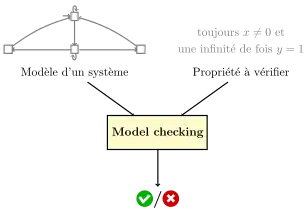
En informatique, la vérification de modèles, ou model checking en anglais, est le problème suivant : vérifier si le modèle d'un système (souvent informatique ou électronique) satisfait une propriété. Par exemple, on souhaite vérifier qu'un programme ne se bloque pas, qu'une variable n'est jamais nulle, etc. Généralement, la propriété est écrite dans un langage, souvent en logique temporelle. La vérification est généralement faite de manière automatique. Sur le plan pratique, la vérification de modèles est devenue, au niveau industriel, la méthode de vérification de code et de systèmes matériels la plus populaire et la plus utilisée aujourd'hui.
Histoire
La vérification de modèles s'appuie sur la logique temporelle dont l'un des pionniers est Amir Pnueli, qui reçut le prix Turing en 1996 pour « […] seminal work introducing temporal logic into computing science » (« […] travaux fondateurs qui introduisent la logique temporelle en informatique »)[1]. Le model checking commence avec les travaux d'Edmund M. Clarke, E. Allen Emerson[2] - [3] - [4], Jean-Pierre Queille[5] et Joseph Sifakis[6] au tout début des années 1980. Clarke, Emerson et Sifakis se sont vu attribuer le prix Turing 2007 pour leurs travaux sur le model checking[7] - [8].
Description
Dans cette section, on précise ce que l'on entend par modèle et propriété puis par le problème de model checking.
Modèle

Le système est modélisé par un système de transition d'états. Il s'agit d'un graphe orienté : un sommet représente un état du système[9] et chaque arc représente une transition[10], c'est-à-dire une évolution possible du système d'un état donné vers un autre état. Chaque état du graphe orienté est étiqueté par l'ensemble des propositions atomiques vraies à ce point d'exécution (par exemple, i=2, le processeur 3 est en attente, etc.). Un tel graphe est aussi appelé une structure de Kripke.
Exemple du distributeur de boissons
On donne ici l'exemple d'un distributeur de boissons qui peut être dans 4 états[11] : attente d'une pièce de monnaie, sélection d'une boisson, distribution d'une bouteille d'eau minérale et distribution d'une bouteille de jus d'orange.
Exemple de l'ascenseur
L'état du système est décrit par le niveau courant de l'ascenseur entre 0 et 3, l'état des appels (4 boutons, un par étage) et si l'ascenseur bouge et s'il patrouille vers le haut ou vers le bas[12] (il y a donc 4 × 2⁴ × 2 × 2 = 256 états).
Propriété
La propriété à vérifier est écrite par une formule de logique temporelle. Par exemple, si l'on souhaite vérifier que x = 0 une infinité de fois, on peut écrire la formule GF(x = 0) qui se lit « toujours, dans le futur, x = 0 ». On distingue :
- les propriétés de sécurité (safety en anglais), comme « l'ascenseur bouge toujours avec les portes fermées » ;
- les propriétés de vivacité (liveneness en anglais), comme « si l'ascenseur est appelé à un certain étage, alors il ira à cet étage ».
Dwyer et al. ont identifié 55 types de spécification en logique temporelle linéaire qui apparaissent dans des applications industrielles[13].
Exemple du distributeur de boissons
Par exemple, (GFa → (G(s → F(e ou j))) (si la machine attend une infinité de fois une pièce, alors toujours, dès que l'on sélectionne une boisson, dans le futur, une boisson (eau minérale ou jus d'orange) est délivrée) est une propriété vraie pour le distributeur de boissons.
Problème du model checking
L'entrée du problème du model checking est un modèle (typiquement un système de transition d'états) et une propriété (typiquement écrite dans une logique temporelle). En sortie, on souhaite savoir si la propriété est vérifiée et, le cas échéant, un contre-exemple d'une exécution du système qui falsifie la propriété.
Algorithmes
Méthodes explicites
Pour des propriétés de sûreté (toujours, p est fausse), on peut faire un parcours en profondeur du graphe et vérifier que chaque état vérifie p. Des algorithmes d'étiquetage existent pour la logique temporelle arborescente (en) (CTL). D'autres méthodes sont fondées sur les automates. On transforme la négation de la formule à vérifier en un automate puis on fait le produit cartésien synchrone de l'automate et du modèle. On se ramène alors à tester si le langage de l'automate produit est vide ou non.
Méthodes symboliques
Parcourir (ou énumérer) explicitement tous les mondes de la structure de Kripke peut être coûteux, c'est pourquoi des méthodes symboliques, introduites par Ken McMillan et Ed Clarke,sont plus pertinentes. Une approche, répandue pour la vérification de propriétés exprimées dans la logique temporelle arborescente, est fondée sur la représentation symbolique du modèle. De nombreuses méthodes de représentation d'ensembles d'états ont vu le jour. La plus connue utilise les diagrammes de décision binaire (BDD).
Discussions
Model checking borné
Au lieu de considérer l'ensemble des traces d'exécution du système, on peut se limiter à des traces finies, de longueur bornée : c'est le model checking borné[14]. L'existence d'une trace vérifiant une certaine propriété est équivalente à la satisfiabilité d'une certaine formule booléenne. En effet, si un état du système est décrit par un k-uplet de booléens, et que l'on s'intéresse aux traces de longueur bornée par un certain n, on se ramène au problème de la satisfiabilité d'une formule propositionnelle (problème SAT). Plus précisément, si une formule identifie les états initiaux du système, une formule les états dont on veut tester l'accessibilité, et une formule est une relation de transition, alors on considère la formule booléenne où sont des propositions atomiques qui représentent l'état à l'étape i de l'exécution du système. Il existe divers logiciels, appelés solveurs SAT, qui peuvent décider « efficacement en pratique » le problème SAT. De plus, ces logiciels fournissent habituellement un exemple de valuation satisfaisant la formule en cas de succès. Certains peuvent produire des éléments d'une preuve de non-satisfiabilité en cas d'échec.
Une évolution récente est l'ajout, en sus de variables booléennes, de variables entières ou réelles. Les formules atomiques ne sont alors plus seulement les variables booléennes, mais des prédicats atomiques sur ces variables entières ou réelles, ou plus généralement des prédicats pris dans une théorie (par exemple , etc.). On parle alors de satisfiabilité modulo une théorie (par exemple, on pourra considérer comme prédicats atomiques les égalités et inégalités linéaires).
Autres modèles
Le modèle peut être plus riche que des automates finis. Il existe par exemple du model checking sur des automates temporisés. Aussi, le concept de model checking se généralise en logique mathématique. Par exemple, la vérification de structures avec une formule de la logique du premier ordre est PSPACE-complet ; de même pour une formule de la logique monadique du second ordre. La vérification de structures automatiques avec une formule du premier ordre est décidable.
Abstraction
Des techniques comme CEGAR (Counterexample-Guided Abstraction Refinement, « raffinement de l'abstraction guidé par les contre-exemples »)[15] permettent de transformer un programme (écrit en C par exemple) en un modèle abstrait puis de raffiner successivement le modèle s'il est trop grossier.
Logique pour les systèmes multi-agents
Dans les systèmes multi-agents, on s'intéresse à des propriétés épistémiques comme « l'agent sait que x = 0 » d'où l'utilisation de logique épistémique et de logiques qui mélangent logique temporelle et épistémique[16]. On s'intéresse à raisonner sur l'existence de stratégies dans un jeu : il existe des logiques pour écrire des propriétés sur les jeux comme « l'agent a une stratégie pour qu'un jour x = 0 » (alternating-time temporal logic (en))[17].
Outils
- alloy[18] ;
- ARC[19] ;
- uPPAAL[20] ;
- APMC[21] ;
- cADP[22] ;
- csml, Mcb[23] ;
- cWB ;
- loTREC ;
- smv[24] ;
- spin[25] - [26] ;
- spot[27] ;
- nuSMV[28] ;
- tina[29] ;
- ROMEO.
- PAT
Depuis 2011, les outils qui le souhaitent participent au Model Checking Contest[30] (MCC), compétition internationale scientifique permettant de comparer les performances des « model checkers » sur différents types de calculs.
Complexité
Un aspect important de la recherche en model checking est de démontrer qu'une certaine classe de propriétés, ou une certaine logique, est décidable, ou que sa décision appartient à une certaine classe de complexité. La table suivante indique les complexités du model checking pour les trois logiques temporelles LTL, CTL et CTL*. La quantité |M| est la taille du modèle représenté explicitement. La quantité |φ| est la taille de la spécification en logique temporelle. La complexité de programme évalue la complexité du model checking lorsque la formule temporelle est fixée[31].
| Logique temporelle | Complexité temporelle d'un algorithme | Complexité du model checking | Complexité de programme du model checking |
|---|---|---|---|
| LTL | O(|M| ×2|φ|) | PSPACE-complet[32] | NLOGSPACE-complet |
| CTL | O(|M| ×|φ|) | P-complet | NLOGSPACE-complet |
| CTL* | O(|M| ×2|φ|) | PSPACE-complet | NLOGSPACE-complet |
Orna Kupferman et Moshe Y. Vardi ont introduit le problème du model checking de systèmes ouverts, abrégé en module checking[33]. En module checking, l'entrée du problème est un système de transition où certains états sont contrôlés par le système proprement dit, et d'autres sont contrôlés par l'environnement. Une propriété temporelle est vraie dans un tel système de transition si elle est vraie quels que soient les choix de l'environnement. Plus précisément, étant donné un système de transition M, on considère son dépliage VM, qui est un arbre infini. Une propriété est vraie dans ce système si elle est vraie dans tout arbre obtenu en élaguant/supprimant de VM certains sous-arbres dont la racine est un successeur d'un état contrôlé par l'environnement. Pour le module checking, Orna Kupferman et Moshe Y. Vardi ont montré que les complexités atteignent celle du problème de satisfiabilité dans les logiques correspondantes :
| Logique temporelle | Complexité du module checking | Complexité de programme du module checking |
|---|---|---|
| LTL | PSPACE-complet | NLOGSPACE-complet |
| CTL | EXPTIME-complet | P-complet |
| CTL* | 2EXPTIME-complet | P-complet |
Allur et al. ont étudié le model checking avec une extension de CTL et CTL* pour raisonner sur des stratégies dans un système multi-agent[17]. La table suivante donne les résultats de complexité pour le model checking sur ATL et ATL*.
| Logique temporelle | Complexité du model checking | Complexité de programme du module checking |
|---|---|---|
| ATL | P-complet | NLOGSPACE-complet |
| ATL* | 2EXPTIME-complet | P-complet |
Comme le signalent Allur et al.[17], le problème de model checking d'ATL* est proche du problème de synthèse LTL qu'ont développé Pnueli et Rosner[34], lui 2EXPTIME-complet également.
Algorithmes efficaces
Un autre aspect de la recherche en model checking est de rechercher des algorithmes efficaces sur des cas intéressants en pratique, de les implémenter, et de les appliquer à des problèmes réels.
Notes et références
- (en) « Amir Pnueli », Association for Computing Machinery.
- E. Allen Emerson et Edmund M. Clarke, « Characterizing correctness properties of parallel programs using fixpoints », Automata, Languages and Programming, (DOI 10.1007/3-540-10003-2_69).
- Edmund M. Clarke, E. Allen Emerson: "Design and Synthesis of Synchronization Skeletons Using Branching-Time Temporal Logic". Logic of Programs 1981: 52-71.
- E. M. Clarke, E. A. Emerson et A. P. Sistla, « Automatic verification of finite-state concurrent systems using temporal logic specifications », ACM Transactions on Programming Languages and Systems, vol. 8, no 2, , p. 244 (DOI 10.1145/5397.5399).
- Il est en particulier l'auteur de la première version du système CESAR : Jean-Pierre Queille, « The CESAR System: An Aided Design and Certification System. », Proceedings of the 2nd International Conference on Distributed Computing Systems, Paris, France, IEEE Computer Society,
- J. P. Queille et J. Sifakis, « Specification and verification of concurrent systems in CESAR », International Symposium on Programming, (DOI 10.1007/3-540-11494-7_22).
- (en) Press Release: ACM Turing Award Honors Founders of Automatic Verification Technology.
- USACM: 2007 Turing Award Winners Announced.
- En terminologie des structures de Kripke, on parle d'un monde.
- En terminologie des structures de Kripke, on parle d'accessibilité.
- Christel Baier et Joost-Pieter Katoen, Principles of Model Checking (Representation and Mind Series), The MIT Press, , 975 p. (ISBN 978-0-262-02649-9 et 0-262-02649-X, lire en ligne).
- « An introduction to model checking ».
- Matthew B. Dwyer, George S. Avrunin et James C. Corbett, « Patterns in Property Specifications for Finite-state Verification », Proceedings of the 21st International Conference on Software Engineering, ACM, iCSE '99, , p. 411–420 (ISBN 1581130740, DOI 10.1145/302405.302672, lire en ligne, consulté le )
- (en) Edmund Clarke, Armin Biere, Richard Raimi et Yunshan Zhu, « Bounded Model Checking Using Satisfiability Solving », Formal Methods in System Design, vol. 19, no 1, , p. 7–34 (ISSN 0925-9856 et 1572-8102, DOI 10.1023/A:1011276507260, lire en ligne, consulté le )
- (en) Edmund Clarke, Orna Grumberg, Somesh Jha et Yuan Lu, Counterexample-Guided Abstraction Refinement, Springer Berlin Heidelberg, coll. « Lecture Notes in Computer Science », (ISBN 978-3-540-67770-3 et 9783540450474, lire en ligne), p. 154–169.
- (en) Alessio Lomuscio et Wojciech Penczek, Symbolic Model Checking for Temporal-Epistemic Logic, Springer Berlin Heidelberg, coll. « Lecture Notes in Computer Science », (ISBN 978-3-642-29413-6 et 9783642294143, lire en ligne), p. 172–195.
- Rajeev Alur, Thomas A. Henzinger et Orna Kupferman, « Alternating-time Temporal Logic », J. ACM, vol. 49, , p. 672–713 (ISSN 0004-5411, DOI 10.1145/585265.585270, lire en ligne, consulté le ).
- Alloy.
- AltaRica.
- UPPAAL.
- Ix-labs/apmc, ix-labs, (lire en ligne)
- CADP.
- Csml, Mcb.
- Smv.
- Spin.
- Gerard Holzmann, Spin Model Checker, the : Primer and Reference Manual, Addison-Wesley Professional, , 596 p. (ISBN 0-321-22862-6, lire en ligne).
- Spot.
- NuSMV.
- Tina.
- Model Checking Contest.
- (en) Moshe Y. Vardi, Logics for Concurrency, Springer, Berlin, Heidelberg, coll. « Lecture Notes in Computer Science », (ISBN 3-540-60915-6, DOI 10.1007/3-540-60915-6_6, lire en ligne), p. 238–266
- A. P. Sistla et E. M. Clarke, « The Complexity of Propositional Linear Temporal Logics », J. ACM, vol. 32, no 3, , p. 733–749 (ISSN 0004-5411, DOI 10.1145/3828.3837, lire en ligne, consulté le )
- (en) Orna Kupferman et Moshe Y. Vardi, « Module checking », Computer Aided Verification, Springer, Berlin, Heidelberg, lecture Notes in Computer Science, , p. 75–86 (ISBN 3540614745, DOI 10.1007/3-540-61474-5_59, lire en ligne, consulté le )
- (en) Amir Pnueli et Roni Rosner, « On the synthesis of an asynchronous reactive module », Automata, Languages and Programming, Springer, Berlin, Heidelberg, lecture Notes in Computer Science, , p. 652–671 (ISBN 9783540513711, DOI 10.1007/BFb0035790, lire en ligne, consulté le )
Voir aussi
Articles connexes
En français
En anglais
- (en) E. M. Clarke, E. A. Emerson et A. P. Sistla, « Automatic verification of finite state concurrent systems using temporal logic », ACM Trans. on Programming Languages and Systems, vol. 8, no 2, , p. 244–263 (DOI 10.1145/5397.5399)
- (en) Kenneth L. McMillan, Symbolic Model Checking, Kluwer, , 194 p. (ISBN 978-0-7923-9380-1 et 0-7923-9380-5, lire en ligne)
- (en) Edmund M. Clarke, Jr., Orna Grumberg et Doron A. Peled, Model Checking, Cambridge (Mass.), MIT Press, , 314 p. (ISBN 0-262-03270-8)
- (en) Michael Huth et Mark Ryan, Logic in Computer Science : Modelling and Reasoning About Systems, CUP, (DOI 10.2277/052154310X)






