Logique monadique du second ordre

En logique mathématique et en informatique théorique, la logique monadique du second ordre[1] (abrégé en MSO pour monadic second order) est l'extension de la logique du premier ordre avec des variables dénotant des ensembles. De manière équivalente, c'est le fragment de la logique du second ordre où les quantifications du second ordre ne portent que sur des prédicats unaires (d'où le terme monadique), c'est-à-dire sur des ensembles. Par exemple :

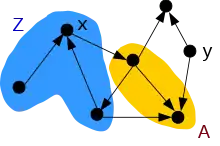
$\exists Z(\exists u,u\in Z)\land \forall x,(x\in Z\rightarrow \exists y,({\text{fils}}(x,y)\land y\in Z))$ est une formule de MSO et elle se lit « il existe un ensemble Z tel qu'il existe un élément u qui appartient à Z et pour tout x, si x est dans Z, alors il existe y tel que y est fils de x et y est dans Z ». Ce n'est pas une formule de la logique du premier ordre car il y a une quantification du second ordre sur Z ;
Toutes les formules de la logique du premier ordre sont des formules de MSO ;
La formule $\exists R,\exists x,\forall y,R(x,y)$ n'est pas une formule de MSO car il y a une quantification sur un prédicat binaire R.

En logique monadique du second ordre, il y a des variables du premier ordre (x, y, etc.) qui représentent des éléments du domaine et des variables du second ordre (A, Z, etc.) qui représentent des sous-ensembles d'éléments.

Le problème de satisfiabilité de la logique du premier ordre étant indécidable, comme MSO est une extension conservatrice de la logique du premier ordre, le problème de satisfiabilité de MSO est aussi indécidable. Mais selon Yuri Gurevich[2], MSO est une source de théories logiques à la fois expressives et décidables.

Exemples de formules

La formule qui définit la récurrence, $\forall X,(X(0)\land (\forall y,X(y)\rightarrow X(y+1)))\rightarrow (\forall z,X(z))$ et qui se lit « pour tout ensemble X, si 0 appartient à X, et si pour tout y, y appartient à X implique y+1 appartient à X alors pour tout z, z appartient à X » est une formule de MSO. Les quantifications « pour tout y » et « pour tout z » sont des quantifications du premier ordre. La quantification « pour tout X » est une quantification du second ordre.

Toutes les formules de la logique du premier ordre sont des formules de MSO.

MSO et graphes

Exemple de graphe non connexe. Les variables du premier ordre x et y dénotent des sommets. La variable du second ordre Z dénote un ensemble de sommets (en bleu).

Par exemple,

C_{1}

(respectivement

C_{2}

C_{3}

) est interprété par l'ensemble des sommets rouges (respectivement bleus et verts).

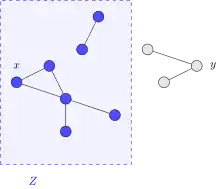
MSO a été défini sur des classes de graphes (par exemple, non orientés). Par exemple, on peut exprimer en MSO qu'un graphe n'est pas connexe[3] : $\exists Z,(\exists x,x\in Z\land \exists y,y\not \in Z)\land (\forall u,v,{\text{arête}}(u,v)\rightarrow (u\in Z\leftrightarrow v\in Z))$ qui se lit « il existe un ensemble de sommets Z tel qu'il existe un sommet x contenu dans Z et un sommet y en dehors de Z et tel que si deux sommets u et v sont reliés par une arête, alors u est dans Z si et seulement si v est dans Z » (voir figure à droite). La connexité n'est pas définissable en logique du premier ordre (c'est une conséquence du théorème de compacité de la logique du premier ordre[4]). Ainsi MSO est strictement plus expressive que la logique du premier ordre sur les graphes.

Sur une classe finie, MSO et la logique du premier ordre ont une expressivité équivalente. Il existe des classes infinies où MSO et la logique du premier ordre ont une expressivité équivalente[5] - [6].

Le théorème de Courcelle est un résultat algorithmique sur MSO et les graphes : toute propriété de MSO est décidable en temps linéaire dans la classe des graphes avec un treewidth borné[3]. Par exemple, d'après le théorème de Courcelle, savoir si un graphe est coloriable avec 3 couleurs est décidable en temps linéaire sur la classe des graphes avec un treewidth borné. En effet, on peut exprimer en MSO qu'un graphe est coloriable avec trois couleurs avec la formule suivante : $\exists C_{1},\exists C_{2},\exists C_{3},\left(\forall s,\bigvee _{i=1}^{3}C_{i}(s)\right)\land \left(\forall s\bigwedge _{i,j=1 \atop i\neq j}^{3}(\lnot C_{i}(s)\lor \lnot C_{j}(s))\right)\land \left(\forall s,t,{\text{arête}}(s,t)\rightarrow \bigwedge _{i=1}^{3}(\lnot C_{i}(s)\lor \lnot C_{i}(t))\right)$ . La formule se lit « il existe des ensembles de sommets C1, C2, C3 qui forment une partition du graphe et tels que deux sommets adjacents ne soient pas dans un même Ci ». Par contre, le problème de décision qui consiste à savoir si n'importe quel graphe est coloriable avec 3 couleurs est un problème NP-complet.

Théorie des langages

La structure sur laquelle est définie MSO change grandement les résultats de définissabilité, de calculabilité, et de complexité.

Mots finis

Büchi a démontré qu'un langage de mots finis est régulier si et seulement s'il est décrit par une formule de MSO sur les mots. MSO est strictement plus expressive que la logique du premier ordre sur les mots finis : la classe des langages de mots finis définis par la logique du premier ordre est la classe des langages sans étoile[7] - [8].

Mots infinis

Büchi a aussi démontré qu'un langage est régulier si et seulement s'il est décrit par une formule de MSO sur les mots.

S1S (pour second-order with 1 successor) est une variante de MSO interprétée sur le domaine des entiers, avec un prédicat pour le successeur et un pour l'ordre[2]. Büchi a démontré en 1962 que S1S est décidable en établissant une correspondance entre la satisfiabilité d'une formule de S1S et la vacuité d'un automate de Büchi[9]. Elgot et Rabin ont démontré que l'on peut ajouter à S1S le prédicat unaire « être un nombre factoriel » ou « être une puissance de $k$ » tout en restant décidable[10]. Par contre, si on ajoute la fonction « fois 2 » au langage, on obtient toute l'arithmétique sur les entiers avec addition et multiplication et on obtient une logique indécidable.

Arbres binaires

On appelle S2S (pour second-order with 2 successors) la variante de MSO pour parler de propriétés sur le modèle de l'arbre binaire infini. Rabin a montré que l'on peut plonger les MSO sur les arbres d'arité 3, 4 et même les arbres d'arité infinie dénombrable dans S2S[11]. Rabin a démontré la décidabilité de S2S par réduction à la vacuité d'un automate d'arbre infini. Par contre, la logique monadique du second ordre sur l'arbre binaire infini avec en plus la relation « même niveau » est indécidable[12].

Version faible

Une variante de MSO, dite faible (et notée WMSO pour weak MSO), a été considérée où la quantification du second ordre porte sur des sous-ensembles finis.

WS1S

WS1S (pour weak second-order with 1 successor) est une variante de S1S où la quantification du second ordre porte uniquement sur les sous-ensembles finis. La décidabilité de WS1S a été démontré avant celle de S1S, par Büchi en 1960[13] et Algot en 1961[14]. La preuve de décidabilité de WS1S s'obtient directement de celle de S1S puisque WS1S peut être vu comme un fragment syntaxique de S1S (on peut exprimer la finitude d'un ensemble dans S1S). On peut démontrer que l'arithmétique de Presburger est décidable en transformant une formule de l'arithmétique de Presburger en une formule de WS1S.

Büchi[15] a montré qu'il y a équivalence, pour tout langage de mots infinis L, entre :

L est définissable par une propriété S1S ;
L est définissable par une propriété WS1S ;
L est reconnaissable par un automate de Büchi.

Les équivalences sont effectives : on transforme une formule S1S en un automate de Büchi. Ainsi, la logique S1S (et WS1S) est décidable. La logique S1S est de complexité non élementaire[16].

WS2S

WS2S (pour weak second-order with 2 successors) est une variante de S2S où la quantification du second ordre est uniquement sur les sous-ensembles finis. WS2S est décidable. WS2S est strictement plus faible que S2S. L'inclusion WS2S ⊆ S2S est stricte, en effet : pour tout langage L d'arbres binaires infinis, on a équivalence entre[17] - [18] :

L et son complémentaire sont reconnaissables par un automate d'arbres avec condition de Büchi ;
L est définissable dans WS2S.

Plus précisément, le langage défini par « il y a un chemin contenant une infinité de b » est reconnaissable par un automate de Büchi alors que son complémentaire ne l'est pas[19]. Ainsi, ce langage est définissable dans S2S, mais pas dans WS2S.

Théorie des groupes

MSO sur les groupes abéliens ordonnés où la quantification du second ordre est restreinte aux sous-groupes convexes est décidable[20].

Invariance par bisimulation

À l'instar du théorème de Van Benthem qui dit que toute formule du première ordre $\phi (x)$ invariante par bisimulation est équivalente à (la traduction standard d') une formule de la logique modale, Janin et Walukiewicz ont démontré que toute formule de MSO invariante par bisimulation est équivalente à une formule du mu-calcul[21].

Il est folklore (voir[22]) d'avoir la variante du théorème de Van Benthem suivante pour WMSO sur les arbres à arité fixée : toute formule de WMSO sur les arbres d'arité k invariante par bisimulation est équivalente à une formule du fragment mu-calcul sans alternance (Arnold et Niwinski ont donné la preuve complète dans le cas des arbres binaires, c'est-à-dire pour WS2S[23]).

Le résultat est plus compliqué pour les arbres d'arités quelconques non fixées. D'une part, il existe une autre variante de MSO qui correspond au fragment sans alternance du mu-calcul[24]. D'autre part, il existe un fragment du fragment du mu-calcul sans alternance qui correspond WMSO invariant par bisimulation[22].

Axiomatisation

MSO sur les mots infinis peut être complètement axiomatisée[25]. En partant du système d'axiomatisation de la logique du premier ordre, il suffit d'ajouter le schéma d'axiomes de compréhension ainsi qu'une version au second ordre de l'axiome de récurrence de Peano.

Nombre d'alternances entre quantificateurs

Selon la structure sur laquelle MSO est interprétée, le nombre d'alternances entre quantificateurs existentiels et universels du second ordre nécessaires pour obtenir l'expressivité maximale de la logique varie. Dans l'interprétation de MSO sur les arbres infinis, toute formule MSO est équivalente à une formule utilisant deux alternances de quantificateurs monadiques[26]. Dans l'interprétation sur des modèles finis à deux dimensions et coloriés (pictures model), une seule alternance suffit[27]. Dans le cas des structures finies, il n'est par contre pas possible de restreindre le nombre d'alternances[28].

Compacité de MSO

La logique monadique du second ordre est compacte.

Voir aussi

Logique monadique du premier ordre

Mu-calcul

Notes et références

Professor Bruno Courcelle et Dr Joost Engelfriet, Graph Structure and Monadic Second-Order Logic : A Language-Theoretic Approach, Cambridge University Press, 1^er janvier 2012, 728 p. (ISBN 978-0-521-89833-1 et 0-521-89833-1, lire en ligne).
(en) Y. Gurevich, « Monadic Second-Order Theories », dans J. Barwise, S. Feferman, Model-Theoretic Logics, New York, Springer-Verlag, 1985, 479-506 p. (lire en ligne).
(en) Bruno Courcelle, Automata, Languages and Programming, Springer Berlin Heidelberg, coll. « Lecture Notes in Computer Science », 7 juillet 2008 (ISBN 978-3-540-70574-1 et 9783540705758, DOI 10.1007/978-3-540-70575-8_1#page-1, lire en ligne), p. 1–13.
(en) « Cours sur le théorème de compacité de M. Vardi » [PDF].
A. Dawar et L. Hella, « The Expressive Power of Finitely Many Generalized Quantifiers », Information and Computation, vol. 123,‎ 1^er décembre 1995, p. 172–184 (DOI 10.1006/inco.1995.1166, lire en ligne, consulté le 20 septembre 2016).
Michael Elberfeld, Martin Grohe et Till Tantau, « Where First-Order and Monadic Second-Order Logic Coincide », Proceedings of the 2012 27th Annual IEEE/ACM Symposium on Logic in Computer Science, IEEE Computer Society, lICS '12,‎ 1^er janvier 2012, p. 265–274 (ISBN 9780769547695, DOI 10.1109/LICS.2012.37, lire en ligne, consulté le 20 septembre 2016).
Robert McNaughton et Seymour A. Papert, Counter-Free Automata (M.I.T. Research Monograph No. 65), The MIT Press, 1^er janvier 1971, 163 p. (ISBN 0-262-13076-9, lire en ligne).
M. P. Schützenberger, « On finite monoids having only trivial subgroups », Information and Control, vol. 8,‎ 1^er avril 1965, p. 190–194 (DOI 10.1016/S0019-9958(65)90108-7, lire en ligne, consulté le 20 septembre 2016).
(en) J. Richard Büchi, « On a decision method in restricted second order arithmetic », dans S. Mac Lane, D. Siefkes, The Collected Works of J. Richard Büchi, New York, Springer, 1990 (ISBN 978-1-4613-8930-9).
(en) Calvin C. Elgot et Michael O. Rabin, « Decidability and Undecidability of Extensions of Second (First) Order Theory of (Generalized) Successor », Journal of Symbolic Logic, vol. 31,‎ 1^er juin 1966, p. 169–181 (ISSN 0022-4812 et 1943-5886, lire en ligne, consulté le 20 septembre 2016).
(en) Rabin M. O., « Decidability of second order theories and automata on infinite trees », Transactions of the American Mathematical Society, vol. 141,‎ 1969, p. 1-35.
Wolfgang Thomas, « Automata on infinite objects », dans Handbook of theoretical computer science (volume B), MIT Press, 1991, 133–191 p. (ISBN 0444880747, lire en ligne)
(en) J. Richard Büchi, « Weak Second-Order Arithmetic and Finite Automata », Mathematical Logic Quarterly, vol. 6,‎ 1^er janvier 1960, p. 66–92 (ISSN 1521-3870, DOI 10.1002/malq.19600060105, lire en ligne, consulté le 20 septembre 2016).
« Decision Problems of Finite Automata Design and Related Arithmetics on JSTOR », sur www.jstor.org (consulté le 20 septembre 2016).
« Büchi, J. R. (1962). On a decision method in restricted second order arithmetic. In E. Nagel, P. Suppes, & A. Tarski (Eds.), Logic, methodology and philosophy of science (pp. 1-11). Stanford Stanford University Press. - References - Scientific Research Publishing », sur www.scirp.org (consulté le 12 février 2018)
(en) « Luke Ong - Automata, Logic and Games: Theory and Application 1. Büchi Automata and S1S ».
(en) Michael O. Rabin, « Weakly Definable Relations and Special Automata », Mathematical Logic and Fondations of Set Theory, North-Holland, vol. 59,‎ 1^er janvier 1970, p. 1–23 (ISSN 0049-237X, DOI 10.1016/S0049-237X(08)71929-3, lire en ligne, consulté le 12 février 2018)
(en) Mark Weyer, Automata Logics, and Infinite Games, Springer, Berlin, Heidelberg, coll. « Lecture Notes in Computer Science », 2002 (ISBN 3-540-36387-4, DOI 10.1007/3-540-36387-4_12, lire en ligne), p. 207–230, Theorem 12.25
(en) Frank Nießner, Automata Logics, and Infinite Games, Springer, Berlin, Heidelberg, coll. « Lecture Notes in Computer Science », 2002 (ISBN 3-540-36387-4, DOI 10.1007/3-540-36387-4_8, lire en ligne), p. 135–152, Theorem 8.6
Yuri Gurevich, « Expanded theory of ordered Abelian groups », Annals of Mathematical Logic, vol. 12,‎ 1^er décembre 1977, p. 193–228 (DOI 10.1016/0003-4843(77)90014-6, lire en ligne, consulté le 20 septembre 2016).
(en) David Janin et Igor Walukiewicz « On the Expressive Completeness of the Propositional Mu-Calculus With Respect to Monadic Second Order Logic » (1996) (lire en ligne, consulté le 23 juillet 2017)
—CONCUR '96: Concurrency Theory
— « (ibid.) », dans Lecture Notes in Computer Science, vol. 1119, Springer.
Facundo Carreiro, Alessandro Facchini, Yde Venema et Fabio Zanasi, « Weak MSO: Automata and Expressiveness Modulo Bisimilarity », Proceedings of the Joint Meeting of the Twenty-Third EACSL Annual Conference on Computer Science Logic (CSL) and the Twenty-Ninth Annual ACM/IEEE Symposium on Logic in Computer Science (LICS), ACM, cSL-LICS '14,‎ 1^er janvier 2014, p. 27:1–27:27 (ISBN 9781450328869, DOI 10.1145/2603088.2603101, lire en ligne, consulté le 20 septembre 2016).
« Rudiments of Calculus, 1st Edition | A. Arnold, D. Niwinski », sur store.elsevier.com (consulté le 20 septembre 2016).
A. Facchini, Y. Venema et F. Zanasi, « A Characterization Theorem for the Alternation-Free Fragment of the Modal #x00B5;-Calculus », 2013 28th Annual IEEE/ACM Symposium on Logic in Computer Science (LICS),‎ 1^er juin 2013, p. 478–487 (DOI 10.1109/LICS.2013.54, lire en ligne, consulté le 20 septembre 2016).
C. Riba, « A Model Theoretic Proof of Completeness of an Axiomatization of Monadic Second-Order Logic on Infinite Words », FIP International Federation for Information Processing, Springer Berlin Heidelberg,‎ 1^er juin 2013, p. 310-324 (DOI 10.1007/978-3-642-33475-7_22, lire en ligne, consulté le 21 septembre 2016).
(en) Wolfgang Thomas, Handbook of Formal Languages : Volume 3 Beyond Words (Languages, automata, and logic), Grzegorz Rozenberg, Arto Salomaa.
(en) O. Matz, « One quantifier will do in existential monadic second-order logic over pictures », Mathematical Foundations of Computer Science 1998,‎ august 24–28, 1998, p. 751-759 (ISSN 0302-9743, lire en ligne).
(en) M. Otto, « A note on the number of monadic quantifiers in monadic ∑^1_1 », Information Processing Letters,‎ 24 mars 1995, p. 337-339 (lire en ligne).

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.