ZPP (complexité)
La classe ZPP, est un objet de la théorie de la complexité, en informatique théorique. C'est une classe de problèmes de décision sur machine de Turing probabiliste. L'acronyme ZPP vient de Zero-Error Probabilistic Polynomial time.
Définitions
Il existe plusieurs définitions équivalentes de ZPP. On commence par celle qui lui donne son nom.
Définition par le temps polynomial en espérance
La classe ZPP est l'ensemble des problèmes, ou de façon équivalentes des langages, pour lesquels il existe une machine de Turing probabiliste telle que :
- La machine ne se trompe pas : elle rejette les mots qui ne sont pas dans le langage et accepte ceux qui y appartiennent (comme pour une classe non-probabiliste).
- Le temps de calcul est polynomial en espérance.
Définitions avec la réponse « Do Not Know »
ZPP est la classe des problèmes qui peuvent être résolus sur une machine de Turing probabiliste en temps polynomial ayant les propriétés suivantes :
- Elle répond Yes, No ou Do Not Know.
- Si la réponse est Yes, alors le mot est dans le langage, et si c'est No il n'y est pas.
- Elle répond Do Not Know avec une probabilité inférieure ou égale à 1/2.
La probabilité 1/2 peut de manière équivalente être remplacée par n'importe quel nombre compris entre 0 et 1 strictement.
Définition par intersection
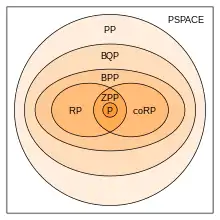
La classe ZPP est aussi l'intersection des classes RP et co-RP :
Histoire
Cette classe a été introduite par J. Gill[1] dans l'article Computational complexity of probabilistic Turing machines, en même temps que la classe RP[2].
Bibliographie
(en) Sanjeev Arora et Boaz Barak, Computational Complexity : A Modern Approach, Cambridge University Press, (ISBN 0-521-42426-7), chap. 7
Lien externe
Notes et références
- Complexity Zoo
- (en) John Gill, « Computational complexity of probabilistic Turing machines », SIAM Journal on Computing, vol. 6, no 4, , p. 675-695

