RP (complexité)

La classe RP est l'ensemble des problèmes, ou de façon équivalente des langages, pour lesquels il existe une machine de Turing probabiliste en temps polynomial qui satisfait les conditions d'acceptation suivantes :

• Si le mot n'est pas dans le langage, la machine le rejette.
• Si le mot est dans le langage, la machine l'accepte avec une probabilité supérieure à 1/2.

On dit que la machine « ne se trompe que d'un côté ».

Pour un polynôme ${\displaystyle T}$ en la taille de l'entrée ${\displaystyle n}$, on définit ${\displaystyle RTIME(T(n))}$, l'ensemble des langages ${\displaystyle L}$ pour lesquels il existe une machine de Turing probabiliste ${\displaystyle M_{L}}$, en temps ${\displaystyle T(n)}$, telle que pour tout mot ${\displaystyle x}$ :

• ${\displaystyle x\notin L\Rightarrow Pr(M_{L}(x)=0)=1}$ .
• ${\displaystyle x\in L\Rightarrow Pr(M_{L}(x)=1)\geq {\frac {1}{2}}}$.

Alors on peut définir RP comme : ${\displaystyle RP=\cup _{p\in N}RTIME(n^{p})}$.

La constante 1/2 est en fait arbitraire, on peut choisir n'importe quel nombre (constant) entre 0 et 1 (exclus)[1].

L'idée est qu'en faisant le calcul indépendamment un nombre polynomial de fois ${\displaystyle p(n)}$, on peut faire chuter la probabilité d'erreur à ${\displaystyle \left({\frac {1}{2}}\right)^{p(n)}}$ dans le cas ${\displaystyle x\in L}$ (tout en gardant une réponse sûre dans le cas ${\displaystyle x\not \in L}$).

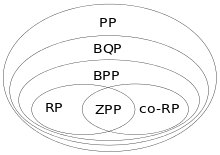
On a la relation suivante avec les classes P et NP : ${\displaystyle P\subseteq RP\subseteq NP}$

Remarquons que cette classe n'est plus intéressante si P=NP.

Valiant et Vazirani ont démontré[2] que ${\displaystyle NP\subseteq RP^{USAT}}$où USAT est le problème SAT, où on promet que la formule booléenne en entrée admet au plus qu'une solution. L'oracle à USAT fonctionne comme suit : il répond positivement sur des formules qui ont exactement une unique solution, il répond négativement sur des formules sans solution, et il répond de manière arbitraire sur les autres formules.

Les inclusions suivantes mettent en jeu les classes ZPP et BPP.

${\displaystyle ZPP\subseteq RP\subseteq BPP}$

Cela vient directement des définitions : ZPP est l'intersection de RP et co-RP et BPP a des conditions d'acceptation moins contraignantes (erreur « des deux côtés »).