BQP

De même que pour les autres classes de complexité probabilistes à erreur bornée, le choix de la probabilité 1/3 d'erreur est arbitraire. On peut exécuter l'algorithme un nombre constant de fois, et prendre la majorité des votes pour obtenir n'importe quelle probabilité de réussite désirée, en utilisant les inégalités de Chernoff. Une analyse détaillée montre que la classe de complexité reste inchangée en autorisant un risque d'erreur inférieur à 1/2 − n^−c d'une part, et supérieur à 2^−nc d'autre part, c étant une constante positive quelconque et n la longueur des données en entrée de l'algorithme.

Inclusions de classes de complexité probabilistes

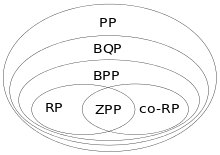
La classe de complexité BQP est l'objet d'études intensives car certains problèmes présentant un intérêt pratique sont démontrés dans BQP, mais sont supposés en dehors de P (classe des problèmes qui peuvent être résolus par l'informatique classique en un temps polynomial).

Parmi les exemples les plus significatifs figurent :

• la décomposition en produit de facteurs premiers (voir Algorithme de Shor) [2] ;
• les logarithmes discrets[2] ;
• la simulation de systèmes quantiques , qui est complet pour les problèmes à promesse de BQP ;
• le calcul des polynômes de Jones pour certaines racines de l'unité.

(en) La classe BQP sur le Complexity Zoo