NL (complexité)

En informatique théorique, plus précisément en théorie de la complexité, NL est une classe de complexité. Cette classe est aussi appelée NLogSpace. C'est l'ensemble des problèmes de décision qui peuvent être décidés par des machines de Turing non déterministes dont l'espace de travail est borné par une fonction logarithmique.

Définition formelle

Si l'on appelle ${\mbox{NSPACE}}(t(n))$ , l'ensemble des problèmes de décision qui peuvent être décidés par des machines de Turing non déterministes utilisant un espace $O(t(n))$ pour une fonction $t$ en la taille de l'entrée $n$ , alors on définit ${\mbox{NL}}={\mbox{NSPACE}}(log(n))$ [1].

Un problème A est NL-dur si tout problème de NL se réduit en espace logarithmique à A. Un problème est NL-complet s'il est dans NL et NL-dur.

Exemples de problèmes NL-complets

Le problème de l'accessibilité : savoir s'il y a un chemin d'une source s à un sommet destination t.

Le problème de l'accessibilité (aussi appelé s-t-accessibilité) qui consiste, étant donné un graphe orienté G, et deux sommets s et t de G, à déterminer s'il y a un chemin de s à t dans G, est NL-complet. Dans ce problème, le graphe est représenté explicitement, avec une matrice d'adjacence ou avec des listes d'adjacences.

Voici d'autres problèmes de décision NL-complets :

2-SAT, la restriction du problème SAT (qui est NP-complet) aux ensembles de clauses d'au plus deux littéraux.
décider si le langage d'un automate fini non-déterministe est vide[2] - [3] - [4].
décider si le langage d'un automate fini déterministe (avec un alphabet non unaire) est vide[3]. Si l'alphabet est unaire, le problème devient L-complet[3].
décider si le langage d'une automate fini déterministe est le langage de tous les mots[3] (attention, si l'automate fini est non-déterministe, le problème devient PSPACE-complet[5]).
décider si le langage d'un automate de Büchi est vide est NL-complet[6].

En 1976, Neil D. Jones, Y. Edmund Lien et William T. Laaser propose des démonstrations de NL-complétude pour plusieurs problèmes[7], à l'instar des problèmes de Karp pour la NP-complétude.

Relations avec les autres classes

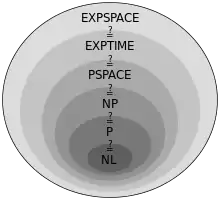
Représentations des inclusions des classes usuelles

La classe NL est une classe relativement petite parmi les classes usuelles. On a notamment NL $\scriptstyle \subseteq$ P.

Comme pour toutes les classes, la variante non déterministe contient la version déterministe, c'est-à-dire que L $\scriptstyle \subseteq$ NL. Au 1^er janvier 2015, l'autre sens NL $\scriptstyle \subseteq$ L est un problème ouvert. Un autre résultat est donné par le théorème de Savitch[8] :

Théorème de Savitch — $\mathbf {NL\subseteq SPACE} (\log ^{2}n)$

Un autre résultat est le théorème dû à Neil Immerman[9] et Róbert Szelepcsényi[10] indépendamment :

Théorème d'Immerman-Szelepcsényi — ${\text{NSPACE}}(s(n))={\text{co-NSPACE}}(s(n))$ , pour toute fonction $s(n)\geq \log n$ , en particulier NL=co-NL

La classe NL est incluse dans NC, même plus précisément dans NC₂[11]. Pour le démontrer, on construit un circuit de taille polynomiale et de profondeur polylogarithmique pour le problème d'accessibilité qui est NL-complet. On montre aussi que la classe NC est stable par réduction logarithmique.

Autres définitions

Définition par certificat

Une définition par certificat est aussi possible, comme pour NP. Les contraintes à ajouter sont les suivantes : le vérificateur est unidirectionnel, c'est-à-dire que la tête de lecture ne peut pas revenir en arrière, et il travaille en espace logarithmique[12].

Définition de complexité descriptive

En complexité descriptive, NL correspond à la logique du premier ordre avec fermeture transitive[13].

Notes et références

Sylvain Perifel, Complexité algorithmique, Ellipses, 2014, 432 p. (ISBN 9782729886929, lire en ligne), chap. 4.3 (« Considérations de base sur l’espace : comparaison avec les classes en temps »), p. 109
« Examen qui pose cette question »
« Space-bounded reducibility among combinatorial problems », Journal of Computer and System Sciences, vol. 11, n^o 1,‎ 1^er août 1975, p. 68–85 (ISSN 0022-0000, DOI 10.1016/S0022-0000(75)80050-X, lire en ligne, consulté le 13 décembre 2017)
« Complexity of universality and related problems for partially ordered NFAs », Information and Computation, vol. 255,‎ 1^er août 2017, p. 177–192 (ISSN 0890-5401, DOI 10.1016/j.ic.2017.06.004, lire en ligne, consulté le 13 décembre 2017)
Alfred V. Aho et John E. Hopcroft, The Design and Analysis of Computer Algorithms, Addison-Wesley Longman Publishing Co., Inc., 1974 (ISBN 0201000296, lire en ligne)
(en) A. Prasad Sistla, Moshe Y. Vardi et Pierre Wolper, « The complementation problem for Büchi automata with applications to temporal logic », Theoretical Computer Science, vol. 49, n^o 2,‎ 1^er janvier 1987, p. 217–237 (ISSN 0304-3975, DOI 10.1016/0304-3975(87)90008-9, lire en ligne, consulté le 7 février 2020) :
« Theorem 2.9 The nonemptiness problem for Büchi automata is logspace complete for NLOGSPACE. »
(en) Neil D. Jones, Y. Edmund Lien et William T. Laaser, « New problems complete for nondeterministic log space », Mathematical Systems Theory, vol. 10, n^o 1,‎ décembre 1976, p. 1–17 (ISSN 0025-5661 et 1433-0490, DOI 10.1007/bf01683259, lire en ligne, consulté le 7 novembre 2018)
Sylvain Perifel, Complexité algorithmique, Ellipses, 2014, 432 p. (ISBN 9782729886929, lire en ligne), chap. 4.5.2 (« Théorème de Savitch »), p. 118.
Neil. Immerman, « Nondeterministic Space is Closed under Complementation », SIAM Journal on Computing, vol. 17, n^o 5,‎ 1^er octobre 1988, p. 935–938 (ISSN 0097-5397, DOI 10.1137/0217058, lire en ligne, consulté le 7 février 2020)
(en) Róbert Szelepcsényi, « The method of forced enumeration for nondeterministic automata », Acta Informatica, vol. 26, n^o 3,‎ 1^er novembre 1988, p. 279–284 (ISSN 1432-0525, DOI 10.1007/BF00299636, lire en ligne, consulté le 7 février 2020)
(en) Papadimitriou, Computational complexity, Theorem 16.1 (p. 395)
Sylvain Perifel, Complexité algorithmique, Ellipses, 2014, 432 p. (ISBN 9782729886929, lire en ligne), chap. 4.5.1 (« Certificats unidirectionnels »), p. 117.
(en) Neil Immerman, « Languages Which Capture Complexity Classes », 15th ACM STOC Symp.,‎ 1983, p. 347-354 (lire en ligne).

Bibliographie

(en) Sanjeev Arora et Boaz Barak, Computational Complexity : A Modern Approach, Cambridge University Press, 2009 (ISBN 0-521-42426-7), chap. 4 (« Space complexity »)

Lien externe

(en) La classe NL sur le Complexity Zoo

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.