Lambda-calcul
Le lambda-calcul (ou λ-calcul) est un système formel inventé par Alonzo Church dans les années 1930, qui fonde les concepts de fonction et d'application. On y manipule des expressions appelées λ-expressions, où la lettre grecque λ est utilisée pour lier une variable. Par exemple, si M est une λ-expression, λx.M est aussi une λ-expression et représente la fonction qui à x associe M.
Le λ-calcul a été le premier formalisme pour définir et caractériser les fonctions récursives : il a donc une grande importance dans la théorie de la calculabilité, à l'égal des machines de Turing[1] et du modèle de Herbrand-Gödel. Il a depuis été appliqué comme langage de programmation théorique et comme métalangage pour la démonstration formelle assistée par ordinateur. Le lambda-calcul peut être typé ou non.
Le lambda-calcul est apparenté à la logique combinatoire de Haskell Curry et se généralise dans les calculs de substitutions explicites.
Présentation informelle
En lambda-calcul, tout est fonction
L'idée de base du lambda-calcul est que tout est fonction. Une fonction est en particulier exprimée par une expression qui peut contenir des fonctions qui ne sont pas encore définies : ces dernières sont alors remplacées par des variables. Il existe une opération de base, appelée application :
Appliquer l'expression (qui décrit une fonction) à l'expression (qui décrit une fonction) se note .
Comment « fabriquer » des fonctions ?
On peut aussi fabriquer des fonctions en disant que si E est une expression[2], on crée la fonction qui à x fait correspondre l'expression E; On écrit λx.E cette nouvelle fonction[3].
Le nom de la variable n'est pas plus important qu'il ne l'est dans une expression comme ∀x P(x) qui est équivalente à ∀y P(y) . Autrement dit si E[y/x] est l'expression E dans laquelle toutes les occurrences de x ont été renommées en y, on considérera que les expressions λx.E et λy.E[y/x] sont équivalentes.
En utilisant les outils dont on vient de se doter, on obtient, par applications et abstractions, des fonctions assez compliquées que l'on peut vouloir simplifier ou évaluer. Simplifier une application de la forme (λx.E) P revient à la transformer en une variante de l'expression E dans laquelle toute occurrence libre de x est remplacée par P. Cette forme de simplification s'appelle une contraction (ou une β-contraction si l'on veut rappeler que l'on applique la règle β du lambda-calcul).
Quelques fonctions
Sur cette base, on peut construire quelques fonctions intéressantes, comme la fonction identité , qui est la fonction qui à fait correspondre , autrement dit la fonction . On peut aussi construire la fonction constante égale à , à savoir .
De là on peut construire la fonction qui fabrique les fonctions constantes, pourvu qu'on lui donne la constante comme paramètre, autrement dit la fonction , c'est-à-dire la fonction qui à fait correspondre la fonction constamment égale à .
On peut aussi par exemple construire une fonction qui permute l'utilisation des paramètres d'une autre fonction, plus précisément si est une expression, on voudrait que fonctionne comme . La fonction est la fonction . Si on applique la fonction à on obtient que l'on peut simplifier en .
Jusqu'à maintenant nous avons été assez informels[4]. L'idée du lambda-calcul consiste à fournir un langage précis pour décrire les fonctions et les simplifier.
Syntaxe
Le lambda calcul définit des entités syntaxiques que l'on appelle des lambda-termes (ou parfois aussi des lambda expressions) et qui se rangent en trois catégories :
- les variables : x, y... sont des lambda-termes ;
- les applications : u v est un lambda-terme si u et v sont des lambda-termes ;
- les abstractions : λ x.v est un lambda-terme si x est une variable et v un lambda-terme.
L’application peut être vue ainsi : si u est une fonction et si v est son argument, alors u v est le résultat de l'application à v de la fonction u.
L’abstraction λ x.v peut être interprétée comme la formalisation de la fonction qui, à x, associe v, où v contient en général des occurrences de x.
Ainsi, la fonction[5] f qui prend en paramètre le lambda-terme x et lui ajoute 2 (c'est-à-dire en notation mathématique courante la fonction f: x ↦ x+2) sera dénotée en lambda-calcul par l'expression λ x.x+2. L'application de cette fonction au nombre 3 s'écrit (λ x.x+2)3 et s'« évalue » (ou se normalise) en l'expression 3+2.
Origine du λ
Alonzo Church connaissait la relation entre son calcul et celui des Principia Mathematica de Russell et Whitehead. Or ceux-ci utilisent la notation pour noter l'abstraction, mais Church utilisa à la place la notation qui devint par la suite [6]. Peano a lui aussi défini l'abstraction dans son Formulaire de mathématique[7], il utilise notamment la notation, pour noter la fonction telle que [8].
Notations, conventions et concepts
Parenthésage
Pour délimiter les applications, on utilise des parenthèses, mais par souci de clarté, on omet certaines parenthèses. Par exemple, on écrit x1 x2 ... xn pour ((x1 x2) ... xn).
Il y a en fait deux conventions :
- Association à gauche, l'expression ((M0 M1) (M2M3)) s'écrit M0 M1 (M2M3). Quand une application s'applique à une autre application, on ne met de parenthèse que sur l'application de droite. Formellement, la grammaire du lambda calcul parenthésé est alors :Λ ::= Var | λ Var. L | Λ L ; L ::= Var | λ Var. L | (Λ L)
- Parenthésage du terme de tête, l'expression ((M0 M1) (M2M3)) s'écrit (M0) M1 (M2) M3. Un terme entre parenthèses est le premier d'une suite d'applications. Ainsi les arguments d'un terme sont facilement identifiables. Formellement, la grammaire du lambda-calcul parenthésé est alors :Λ ::= Var | λ Var. Λ | (Λ) Λ+.
Curryfication
Shönfinkel et Curry ont introduit la curryfication : c'est un procédé pour représenter une fonction à plusieurs arguments. Par exemple, la fonction qui au couple (x, y) associe u est considérée comme une fonction qui, à x, associe une fonction qui, à y, associe u. Elle est donc notée : λx.(λy.u). Cela s'écrit aussi λx.λy.u ou λxλy.u ou tout simplement λxy.u. Par exemple, la fonction qui, au couple (x, y) associe x+y sera notée λx.λy.x+y ou plus simplement λxy.x+y.
Variables libres et variables liées
Dans les expressions mathématiques en général et dans le lambda calcul en particulier, il y a deux catégories de variables : les variables libres et les variables liées (ou muettes). En lambda-calcul, une variable est liée[9] par un λ. Une variable liée a une portée[10] et cette portée est locale. De plus, on peut renommer une variable liée sans changer la signification globale de l'expression entière où elle figure. Une variable qui n'est pas liée est dite libre.
Variables liées en mathématiques
Par exemple dans l'expression , la variable est libre, mais la variable est liée (par le ). Cette expression est « la même » que car était un nom local, tout comme l'est . Par contre ne correspond pas à la même expression car le est libre.
Tout comme l'intégrale lie la variable d'intégration, le lie la variable qui le suit.
Exemples:
- Dans , la variable est liée et la variable est libre. Ce terme est α-équivalent au terme .
- est α-équivalent à .
- est α-équivalent à .
Définition formelle des variables libres en lambda-calcul
On définit l'ensemble VL(t) des variables libres d'un terme t par récurrence :
- si est une variable alors VL() = {}
- si u et v sont des lambda-termes alors VL(u v) = VL(u) ∪ VL(v)
- si est une variable et u un lambda-terme alors VL(λ.u) = VL(u) \{}
Terme clos et terme ouvert
Un terme qui ne contient aucune variable libre est dit clos (ou fermé). On dit aussi que ce lambda-terme est un combinateur (d'après le concept apparenté de logique combinatoire).
Un terme qui n'est pas clos est dit ouvert.
Substitution et α-conversion
L'outil le plus important pour le lambda-calcul est la substitution qui permet de remplacer, dans un terme, une variable par un terme. Ce mécanisme est à la base de la réduction qui est le mécanisme fondamental de l'évaluation des expressions, donc du « calcul » des lambda-termes.
La substitution dans un lambda terme t d'une variable x par un terme u est notée t[x := u]. Il faut prendre quelques précautions pour définir correctement la substitution afin d'éviter le phénomène de capture de variable qui pourrait, si l'on n'y prend pas garde, rendre liée une variable qui était libre avant que la substitution n'ait lieu.
Par exemple, si u contient la variable libre y et si x apparaît dans t comme occurrence d'un sous terme de la forme λy.v, le phénomène de capture pourrait apparaître. L'opération t[x := u] s'appelle la substitution dans t de x par u et se définit par récurrence sur t :
- si t est une variable alors t[x := u]=u si x=t et t sinon
- si t = v w alors t[x := u] = v[x := u] w[x := u]
- si t = λy.v alors t[x := u] = λy.(v[x := u]) si x≠y et t sinon
Remarque : dans le dernier cas on fera attention à ce que y ne soit pas une variable libre de u. En effet, elle serait alors « capturée » par le lambda externe. Si c'est le cas, on renomme y et toutes ses occurrences dans v par une variable z qui n'apparaît ni dans t ni dans u.
L'α-conversion identifie λy.v et λz.v[y := z]. Deux lambda-termes qui ne diffèrent que par un renommage (sans capture) de leurs variables liées sont dits α-convertibles. L'α-conversion est une relation d'équivalence entre lambda-termes.
Exemples :
- (λx.xy)[y := a] = λx.xa
- (λx.xy)[y := x] = λz.zx (et non λ x.xx, qui est totalement différent, cf remarque ci-dessus)
Remarque : l'α-conversion doit être définie avec précaution avant la substitution. Ainsi dans le terme λx.λy.xyλz.z, on ne pourra pas renommer brutalement x en y (on obtiendrait λy.λy.yyλz.z) en revanche on peut renommer x en z.
Définie ainsi, la substitution est un mécanisme externe au lambda-calcul, on dit aussi qu'il fait partie de la méta-théorie. À noter que certains travaux visent à introduire la substitution comme un mécanisme interne au lambda-calcul, conduisant à ce qu'on appelle les calculs de substitutions explicites.
Réductions
Une manière de voir les termes du lambda-calcul consiste à les concevoir comme des arbres ayant des nœuds binaires (les applications), des nœuds unaires (les λ-abstractions) et des feuilles (les variables). Les réductions[11] ont pour but de modifier les termes, ou les arbres si on les voit ainsi ; par exemple, la réduction de (λx.xx)(λy.y) donne (λy.y)(λy.y).
On appelle rédex un terme de la forme (λx.u) v, où u et v sont des termes et x une variable. On définit la bêta-contraction (ou β-contraction) de (λx.u) v comme u[x := v]. On dit qu'un terme C[u] se réduit[12] en C[u'] si u est un rédex qui se β-contracte en u', on écrit alors C[u]→C[u'], la relation → est appelée contraction.
Exemple de contraction :
(λx.xy)a donne (xy)[x := a] = ay.
On note →* la fermeture réflexive transitive[13] de la relation de contraction → et on l'appelle réduction. Autrement dit, une réduction est une suite finie, éventuellement vide, de contractions.
On définit =β comme la fermeture réflexive symétrique et transitive de la contraction et elle est appelée bêta-conversion, β-conversion, ou plus couramment bêta-équivalence ou β-équivalence.
La β-équivalence permet par exemple de comparer des termes qui ne sont pas réductibles l'un envers l'autre, mais qui après une suite de β-contractions arrivent au même résultat. Par exemple (λy.y)x =β (λy.x)z car les deux expressions se contractent pour donner x.
Formellement, on a M =β M' si et seulement si ∃ N1, ..., Np tels que M = N1, M'=Np et, pour tout i inférieur à p et supérieur à 0, Ni→ Ni+1 ou Ni+1→ Ni .
Cela signifie que dans une conversion on peut appliquer des réductions ou des relations inverses des réductions (appelées expansions).
On définit également une autre opération, appelée êta-réduction[14], définie ainsi : λx.ux →η u, lorsque x n'apparait pas libre dans u. En effet, ux s'interprète comme l'image de x par la fonction u. Ainsi, λx.ux s'interprète alors comme la fonction qui, à x, associe l'image de x par u, donc comme la fonction u elle-même.
La normalisation : notions de calcul et de terme en forme normale
Le calcul associé à un lambda-terme est la suite de réductions qu'il engendre. Le terme est la description du calcul et la forme normale du terme[15] (si elle existe) en est le résultat.
Un lambda-terme t est dit en forme normale si aucune bêta-contraction ne peut lui être appliquée, c'est-à-dire si t ne contient aucun rédex, ou encore s'il n'existe aucun lambda-terme u tel que t → u. La structure syntaxique des termes en forme normale est décrite plus loin.
λx.y(λz.z(yz))
On dit qu'un lambda-terme t est normalisable s'il existe un terme u auquel on ne peut appliquer aucune bêta-contraction et tel que t =β u. Un tel u est appelé la forme normale de t.
On dit qu'un lambda-terme t est fortement normalisable si toutes les réductions à partir de t sont finies.
Posons Δ ≡ λx.xx.
- L'exemple par excellence de lambda-terme non fortement normalisable est obtenu en appliquant ce terme à lui-même, autrement dit : Ω = (λx.xx)(λx.xx) = ΔΔ. Le lambda terme Ω n'est pas fortement normalisable car sa réduction boucle indéfiniment sur elle-même. (λx.xx)(λx.xx) → (λx.xx)(λx.xx).
- (λx.x)((λy.y)z) est un lambda-terme fortement normalisable et sa forme normale est .
- (λx.y)(ΔΔ) est normalisable et sa forme normale est , mais il n'est pas fortement normalisable car la réduction du terme (λx.y)(ΔΔ) peut aboutir au terme mais aussi au terme (λx.y)(ΔΔ) si on considère Δ ≡ λx.xx.
- (λx.xxx)(λx.xxx) → (λx.xxx)(λx.xxx)(λx.xxx) → (λx.xxx)(λx.xxx)(λx.xxx)(λx.xxx) → ... crée des termes de plus en plus grands.
Si un terme est fortement normalisable, alors il est normalisable.
Deux théorèmes fondamentaux
Théorème de Church-Rosser : soient t et u deux termes tels que t =β u. Il existe un terme v tel que t →* v et u →* v.
Théorème du losange (ou de confluence) : soient t, u1 et u2 des lambda-termes tels que t →* u1 et t →* u2. Alors il existe un lambda-terme v tel que u1 →* v et u2 →* v.
Grâce au Théorème de Church-Rosser on peut facilement montrer l’unicité de la forme normale ainsi que la cohérence du lambda-calcul (c'est-à-dire qu'il existe au moins deux termes distincts non bêta-convertibles).
Structure des termes en forme normale
On peut décrire la structure des termes en forme normale qui forment l'ensemble . Pour cela on décrit des termes dits neutres qui forment l'ensemble . Les termes neutres sont les termes dans lesquels une variable (par exemple ) est appliquée à des termes en forme normale. Ainsi, par exemple, est neutre si ... sont en forme normale. Les termes en forme normale sont les termes neutres précédés de zéro, un ou plusieurs λ, autrement dit, des abstractions successives de termes en forme normale. Ainsi est en forme normale. On peut décrire les termes en forme normale par une grammaire.
Exemples : est neutre, donc aussi en forme normale. est en forme normale. est neutre. est en forme normale. Par contre, n'est pas en forme normale car il n'est pas neutre et il n'est pas une abstraction d'un terme en forme normale, mais aussi parce qu'il est lui-même un β-rédex, donc β-réductible.
Différents lambda-calculs
Sur la syntaxe et la réduction du lambda-calcul on peut adapter différents calculs en restreignant plus ou moins la classe des termes. On peut ainsi distinguer deux grandes classes de lambda-calculs : le lambda-calcul non typé et les lambda-calculs typés. Les types sont des annotations des termes qui ont pour but de ne garder que les termes qui sont normalisables, éventuellement en adoptant une stratégie de réduction. On espère[16] ainsi avoir un lambda-calcul qui satisfait les propriétés de Church-Rosser et de normalisation.
La correspondance de Curry-Howard relie un lambda calcul typé à un système de déduction naturelle. Elle énonce qu'un type correspond à une proposition et un terme correspond à une preuve, et réciproquement.
Le lambda-calcul non typé
Des codages simulent les objets usuels de l'informatique dont les entiers naturels, les fonctions récursives et les machines de Turing. Réciproquement le lambda-calcul peut être simulé par une machine de Turing. Grâce à la thèse de Church on en déduit que le lambda-calcul est un modèle universel de calcul.
Les booléens
Dans la partie Syntaxe, nous avons vu qu'il est pratique de définir des primitives. C'est ce que nous allons faire ici.
vrai = λab.a
faux = λab.b
Ceci n'est que la définition d'un codage, et l'on pourrait en définir d'autres.
Nous remarquons que : vrai x y →* x et que : faux x y →* y
Nous pouvons alors définir un lambda-terme représentant l'alternative: if-then-else. C'est une fonction à trois arguments, un booléen b et deux lambda termes u et v, qui retourne le premier si le booléen est vrai et le second sinon.
ifthenelse = λbuv.(b u v).
Notre fonction est bien vérifiée: ifthenelse vrai x y = (λbuv.(b u v)) vrai x y ; ifthenelse vrai x y → (λuv.(vrai u v)) x y ; ifthenelse vrai x y →* (vrai x y) ; ifthenelse vrai x y →* ( (λab.a) x y) ; ifthenelse vrai x y →* x.
On verra de la même manière que ifthenelse faux x y →* y.
À partir de là nous avons aussi un lambda-terme pour les opérations booléennes classiques : non = λb.ifthenelse b faux vrai ; et = λab.ifthenelse a b faux (ou bien λab.ifthenelse a b a) ; ou = λab.ifthenelse a vrai b (ou bien λab.ifthenelse a a b).
Les entiers
Ce qui suit est un codage en lambda-calcul des entiers que l'on appelle entiers de Church, du nom de leur concepteur. On pose : 0 = λfx.x, 1 = λfx.f x, 2 = λfx.f (f x), 3 = λfx.f (f (f x)) et d'une manière générale : n = λfx.f (f (...(f x)...)) = λfx.f nx avec f itérée n fois.
Ainsi, l'entier n est vu comme la fonctionnelle qui, au couple ≺f, x≻, associe f n(x).
Quelques fonctions
Il y a deux manières de coder la fonction successeur, soit en ajoutant un f en tête, soit en queue. Au départ nous avons n = λfx.f n x et nous voulons λfx.f n+1 x. Il faut pouvoir rajouter un f soit au début des f (« sous » les lambdas), soit à la fin.
- Si nous choisissons de le mettre en tête, il faut pouvoir entrer « sous » les lambdas. Pour cela, si n est notre entier, on forme d'abord n f x, ce qui donne f n x. En mettant un f en tête, on obtient : f (n f x) → f(f n x) = f n+1 x. Il suffit alors de compléter l'entête pour reconstruire un entier de Church : λfx.f (n f x) = λfx.f n+1 x . Enfin pour avoir la « fonction » successeur, il faut bien entendu prendre un entier en paramètre, donc rajouter un lambda. Nous obtenons λnfx.f(n f x). Le lecteur pourra vérifier que (λnfx.f(n f x)) 3 = 4, avec 3 = λfx.f(f(f x))) et 4 = λfx.f(f(f(f x)))).
- Si par contre nous voulions mettre le f en queue, il suffit d'appliquer n f x non pas à x, mais à f x, à savoir n f (f x), ce qui se réduit à fn (f x) = fn+1 x. On n'a plus qu'à refaire l'emballage comme dans le cas précédent et on obtient λnfx.n f (f x). La même vérification pourra être faite.
Les autres fonctions sont construites avec le même principe. Par exemple l'addition, en « concaténant » les deux lambda-termes : λnpfx.n f (p f x).
Pour coder la multiplication, on utilise le f pour « propager » une fonction sur tout le terme : λnpf.n (p f)
Le prédécesseur et la soustraction ne sont pas simples non plus. On en reparlera plus loin.
On peut définir le test à 0 ainsi : if0thenelse = λnab.n (λx.b) a, ou bien en utilisant les booléens λn.n (λx.faux) vrai.
Les itérateurs
Définissons d'abord une fonction d'itération sur les entiers : itère = λnuv.n u v
v est le cas de base et u une fonction. Si n est nul, on calcule v, sinon on calcule u n(v).
Par exemple l'addition qui provient des équations suivantes
- add(0, p) = p
- add(n+1, p) = add(n,p+1)
peut être définie comme suit. Le cas de base v est le nombre p, et la fonction u est la fonction successeur. Le lambda-terme correspondant au calcul de la somme est donc : add = λnp.itère n successeur p. On remarquera que add n p →* n successeur p.
Les couples
On peut coder des couples par c = λz.z a b où a est le premier élément et b le deuxième. On notera ce couple (a, b). Pour accéder aux deux parties on utilise π1 = λc.c (λab.a) et π2 = λc.c (λab.b). On reconnaîtra les booléens vrai et faux dans ces expressions et on laissera le soin au lecteur de réduire π1(λz.z a b) en a.
Les listes
On peut remarquer qu'un entier est une liste dont on ne regarde pas les éléments, en ne considérant donc que la longueur. En rajoutant une information correspondant aux éléments, on peut construire les listes d'une manière analogue aux entiers : [a1 ; ... ; an] = λgy. g a1 (... (g an y)...). Ainsi : [] = λgy.y ; [a1] = λgy.g a1 y ; [a1 ; a2] = λgy.g a1 (g a2 y).
Les itérateurs sur les listes
De la même manière qu'on a introduit une itération sur les entiers on introduit une itération sur les listes. la fonction liste_it se définit par λlxm.l x m comme pour les entiers. Le concept est à peu près le même mais il y a des petites nuances. Nous allons voir par un exemple.
exemple : La longueur d'une liste est définie par
- longueur ([]) = 0
- longueur (x :: l) = 1 + longueur l
x :: l est la liste de tête x et de queue l (notation ML). La fonction longueur appliquée sur une liste l se code par : λl.liste_it l (λym.add (λfx.f x) m) (λfx.x) ou tout simplement λl.l (λym.add 1 m) 0.
Les arbres binaires
Le principe de construction des entiers, des couples et des listes se généralise aux arbres binaires :
- constructeur de feuille : feuille = λngy.y n
- constructeur de nœud : nœud = λbcgy.g (b g y) (c g y) (avec b et c des arbres binaires)
- itérateur : arbre_it = λaxm.a x m
Un arbre est soit une feuille, soit un nœud. Dans ce modèle, aucune information n'est stockée au niveau des nœuds, les données (ou clés) sont conservées au niveau des feuilles uniquement. On peut alors définir la fonction qui calcule le nombre de feuilles d'un arbre : nb_feuilles = λa.arbre_it a (λbc.add b c) (λn.1), ou plus simplement: nb_feuilles = λa.a add (λn.1)
Le prédécesseur
Pour définir le prédécesseur sur les entiers de Church, il faut utiliser les couples. L'idée est de reconstruire le prédécesseur par itération : pred = λn.π1 (itère n (λc.(π2 c, successeur (π2 c))) (0,0)). Puisque le prédécesseur sur les entiers naturels n'est pas défini en 0, afin de définir une fonction totale, on a ici adopté la convention qu'il vaut 0.
On vérifie par exemple que pred 3 →* π1 (itère 3 (λc.(π2 c, successeur (π2 c))) (0,0)) →* π1 (2,3) →* 2.
On en déduit que la soustraction est définissable par : sub = λnp.itère p pred n avec la convention que si p est plus grand que n, alors sub n p vaut 0.
La récursion
En combinant prédécesseur et itérateur, on obtient un récurseur. Celui-ci se distingue de l'itérateur par le fait que la fonction qui est passée en argument a accès au prédécesseur.
rec = λnfx.π1 (n (λc.(f (π2 c) (π1 c), successeur (π2 c))) (x, 0))
Combinateurs de point fixe
Un combinateur de point fixe permet de construire pour chaque F, une solution à l'équation X = F X . Ceci est pratique pour programmer des fonctions qui ne s'expriment pas simplement par itération, telle que le pgcd, et c'est surtout nécessaire pour programmer des fonctions partielles.
Le combinateur de point fixe le plus simple, dû à Curry, est : Y = λf.(λx.f(x x))(λx.f(x x)). Turing a proposé un autre combinateur de point fixe : Θ = (λx. λy. (y (x x y))) (λx. λy. (y (x x y))).
On vérifie que quel que soit g. Grâce au combinateur de point fixe, on peut par exemple définir une fonction qui prend en argument une fonction et teste si cette fonction argument renvoie vrai pour au moins un entier : teste_annulation = λg.Y (λfn.ou (g n) (f (successeur n))) 0.
Par exemple, si on définit la suite alternée des booléens vrai et faux : alterne = λn.itère n non faux, alors, on vérifie que : teste_annulation alterne →* ou (alterne 0) (Y (λfn.ou (alterne n) (f successeur n)) (successeur 0)) →* ou (alterne 1) (Y (λfn.ou (alterne n) (f successeur n)) (successeur 1)) →* vrai.
On peut aussi définir le pgcd : pgcd = Y (λfnp.if0thenelse (sub p n) (if0thenelse (sub n p) p (f p (sub n p))) (f n (sub p n))).
Connexion avec les fonctions partielles récursives
Le récurseur et le point fixe sont des ingrédients clés permettant de montrer que toute fonction partielle récursive est définissable en λ-calcul lorsque les entiers sont interprétés par les entiers de Church. Réciproquement, les λ-termes peuvent être codés par des entiers et la réduction des λ-termes est définissable comme une fonction (partielle) récursive. Le λ-calcul est donc un modèle de la calculabilité.
Le lambda-calcul simplement typé
On annote les termes par des expressions que l'on appelle des types. Pour cela, on fournit un moyen de donner un type à un terme. Si ce moyen réussit, on dit que le terme est bien typé. Outre le fait que cela donne une indication sur ce que « fait » la fonction, par exemple, elle transforme les objets d'un certain type en des objets d'un autre type, cela permet de garantir la normalisation forte, c'est-à-dire que, pour tous les termes, toutes les réductions aboutissent à une forme normale (qui est unique pour chaque terme de départ). Autrement dit, tous les calculs menés dans ce contexte terminent. Les types simples sont construits comme les types des fonctions, des fonctions de fonctions, des fonctions de fonctions de fonctions vers les fonctions, etc. Quoi qu'il puisse paraître, le pouvoir expressif de ce calcul est très limité (ainsi, l'exponentielle ne peut y être définie, ni même la fonction ).
Plus formellement, les types simples sont construits de la manière suivante:
- un type de base (si on a des primitives, on peut aussi se donner plusieurs types de bases, comme les entiers, les booléens, les caractères, etc. mais cela n'a pas d'incidence au niveau de la théorie).
- si et sont des types, est un type.
Intuitivement, le second cas représente le type des fonctions acceptant un élément de type et renvoyant un élément de type .
Un contexte est un ensemble de paires de la forme où est une variable et un type. Un jugement de typage est un triplet (on dit alors que est bien typé dans ), défini récursivement par:
- si , alors .
- si , alors .
- si et , alors
Si on a ajouté des constantes au lambda calcul, il faut leur donner un type (via ).
Les lambda-calculs typés d'ordres supérieurs
Le lambda-calcul simplement typé est trop restrictif pour exprimer toutes les fonctions calculables dont on a besoin en mathématiques et donc dans un programme informatique. Un moyen de dépasser l'expressivité du lambda-calcul simplement typé consiste à autoriser des variables de type et à quantifier sur elles, comme cela est fait dans le système F ou le calcul des constructions.
Le lambda calcul et les langages de programmation
Le lambda-calcul constitue la base théorique de la programmation fonctionnelle et a ainsi influencé de multiples langages de programmation. Le premier d'entre eux est Lisp qui est un langage non typé. Plus tard, ML et Haskell, qui sont des langages typés, seront développés.
Les indices de de Bruijn
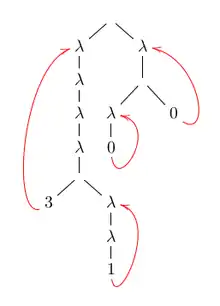
Les indices de de Bruijn[17] - [18] sont une notation du lambda calcul qui permet de représenter par un terme, chaque classe d'équivalence pour l'α-conversion. Pour cela, de Bruijn a proposé de remplacer chaque occurrence d'une variable par un entier naturel[19]. Chaque entier naturel dénote le nombre de λ qu'il faut croiser pour relier l'occurrence à son lieur.
Ainsi le terme λ x. x x est représenté par le terme λ 0 0 tandis que le terme λx. λy. λz .x z (y z) est représenté par λ λ λ 2 0 (1 0), parce que, dans le premier cas, le chemin de x à son lieur ne croise aucun λ, tandis que, dans le deuxième cas, le chemin de x à son lieur croise deux λ (à savoir λy et λz), le chemin de y à son lieur croise un λ (à savoir λz) et le chemin de z à son lieur ne croise aucun λ.
Comme autre exemple, le terme (λ x λ y λ z λ u . (x (λ x λ y. x))) (λ x. (λ x. x) x) et un terme qui lui est α-équivalent, à savoir (λ x λ y λ z λ u . (x (λ v λ w. v))) (λ u. (λ t. t) u) sont représentés par (λ λ λ λ (3 (λ λ 1))) (λ (λ 0) 0) (voir la figure).
Notes
- A. M. Turing, « Computability and λ-Definability », The Journal of Symbolic Logic, vol. 2, no 4, , p. 153–163 (DOI 10.2307/2268280, lire en ligne, consulté le )
- qui peut éventuellement contenir la variable x.
- ce que les mathématiciens auraient écrit .
- En particulier, nous avons édulcoré le problème du remplacement d'une variable par un terme qui pose des problèmes délicats.
- Cette explication semble introduire des constantes entières et des opérations, comme + et *, mais il n'en est rien, car ces concepts peuvent être décrits par des lambda termes spécifiques dont ils ne sont que des abréviations.
- (en) J. Barkley Rosser, « Highlights of the History of the Lambda-Calculus », Annals of the History of Computing, vol. 6, no 4, , p. 338.
- G. Peano, Formulaire de mathématiques : Logique mathématique, t. II, (lire en ligne),
- page 58.
- En mathématiques, les variables sont liées par ∀ ou par ∃ ou par ∫ ... dx.
- La portée est la partie de l'expression où la variable a la même signification.
- Attention « réduction » ne veut pas dire que la taille diminue !
- C[ ] est appelé un contexte.
- De nombreux auteurs notent cette relation ↠.
- Ainsi que son inverse la êta-expansion
- Le terme issu de la réduction à partir duquel on ne peut plus réduire.
- Espoir fondé en général, mais encore faut-il le démontrer !
- De Bruijn, Nicolaas Govert, « Lambda Calculus Notation with Nameless Dummies: A Tool for Automatic Formula Manipulation, with Application to the Church-Rosser Theorem », Elsevier, vol. 34, , p. 381–392 (ISSN 0019-3577, lire en ligne)
- Benjamin Pierce, Types and Programming Language, The MIT Press, (ISBN 0-262-16209-1, lire en ligne), « Chapitre 6: Nameless representation of terms »
- Ceci est une approche assez comparable à celle de Bourbaki qui utilise des « assemblages » et des « liens ».
Bibliographie
- (en) Henk Barendregt, The Lambda-Calculus, volume 103, Elsevier Science Publishing Company, Amsterdam, 1984.
- F Cardone et JR Hindley, Handbook of the History of Logic,, (lire en ligne), « History of lambda-calculus and combinatory logic »
- Marcel Crabbé, Le calcul lambda, Cahiers du centre de logique, numéro 6, 1986.
- Jean-Louis Krivine, Lambda-Calcul, types et modèles, Masson 1991, traduction anglaise accessible sur le site de l'auteur .
- (en) Steven Fortune, Daniel Leivant, Michael O'Donnell, « The Expressiveness of Simple and Second-Order Type Structures » dans Journal of the ACM vol. 30 (1983), p. 151-185.
- (en) Jean-Yves Girard, Paul Taylor, Yves Lafont, Proofs and Types, Cambridge University Press, New York, 1989 (ISBN 0-521-37181-3).
- Pierre Lescanne, « Et si on commençait par les fonctions ! », Images des mathématiques.
- Hervé Poirier, « La Vraie Nature de l'intelligence », dans Science et Vie no 1013 (), p. 38-57.
- Francis Renaud, Sémantique du temps et lambda-calcul, Presses universitaires de France, 1996 (ISBN 2-13-047709 7)

































































