Maille (cristallographie)

• Le contenu de la maille se répète par translation dans les 3 dimensions.
• Le contenu de la maille peut être fait d'un motif qui se répète (à l'intérieur de la maille) par des symétries autres que les translations. Par exemple centres, plans, axes…
• Le contenu d'une maille peut n'être constitué que d'un motif (s'il n y a pas de symétrie).
• La connaissance du motif et des symétries permet de reconstituer le contenu de la maille, la connaissance de la maille permet de reconstruire par translation tout le cristal.

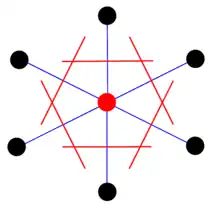
Une maille primitive, ou simple, voire élémentaire, est le motif géométrique le plus simple qui, en se répétant indéfiniment, constitue un réseau cristallin. Les mailles représentées sur la figure de droite sont des mailles primitives.

Une maille primitive contient un nœud du réseau à chaque sommet, mais aucun nœud à l'intérieur de son volume ou de l'une de ses faces.

Maille de Wigner-Seitz.

La Maille de Wigner-Seitz est un type particulier de maille primitive qui est construite comme la région de l'espace la plus proche d'un nœud du réseau que de n'importe quel autre nœud. Elle contient donc un nœud au centre mais aucun nœud aux sommets.

Un algorithme a été trouvé dans les années 1970 pour isoler systématiquement un représentant unique parmi l'infinité de mailles primitives[2], appelé alors maille réduite. La première condition pour qu'une maille élémentaire soit la maille réduite est qu'elle soit basée sur les trois vecteurs de base non-coplanaires les plus petits. Des conditions particulières permettent de traiter le cas des réseaux où cette condition ne suffit pas à déterminer une maille unique. Aujourd'hui, cet algorithme de réduction a été implémenté dans des logiciels qui automatisent la procédure[2].

Maille conventionnelle (rouge) ainsi que quatre mailles primitives (noires) du réseau orthorhombique centré oc à deux dimensions.

La maille conventionnelle est une maille dont les axes sont parallèles aux directions de symétrie du réseau. Dans le cas de réseaux centrés ou à faces centrées, la maille conventionnelle n'est donc pas une maille primitive ; la maille conventionnelle équivaut à un nombre entier de mailles primitives, généralement noté Z.

Les cristaux dont les mailles conventionnelles sont transformées l'une en l'autre en ajoutant ou supprimant des nœuds soit au centre des faces, soit à l'intérieur du volume de la maille, appartiennent à la même famille cristalline.

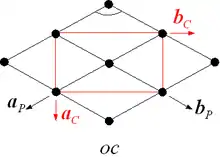
Exemple. Le réseau orthorhombique centré représenté ci-contre possède deux axes de symétrie d'ordre deux : l'un horizontal et l'autre vertical. La maille conventionnelle du réseau (maille rouge dans la figure) possède des côtés parallèles aux axes de symétrie du réseau, tandis que dans la maille primitive correspondante (maille noire dans la figure), les deux directions de symétrie sont bissectrices des axes (a_P et b_P).

Le réseau monoclinique n’ayant qu’une direction de symétrie, sa maille conventionnelle est normalement repérée :

• en prenant la direction de symétrie comme axe b ;
• en choisissant le sommet origine de façon que les axes a et c forment le plus petit angle non-aigu.

Le terme maille élémentaire est le plus utilisé dans la littérature cristallographique francophone. Comme l'adjectif « élémentaire » le suggère, la maille en question ne contient qu'un seul nœud de réseau : il s'agit ainsi d'une maille primitive ou simple. Toutefois, dans l'usage courant le terme est souvent utilisé comme synonyme de maille conventionnelle, qui parfois est une maille multiple. Dans ce cas, on obtient une « maille élémentaire » qui, étant multiple, n'a plus le caractère « élémentaire ». Par exemple, la maille conventionnelle d'un réseau cubique à faces centrées est une maille qui contient quatre nœuds. La maille élémentaire de ce réseau ne coïncide pas avec la maille conventionnelle mais avec la maille rhomboédrique primitive.

La prise en compte du groupe d'espace G du cristal permet une définition plus formelle de la notion de maille. Ce groupe est constitué des opérations de symétrie — isométrie affine — laissant invariant la structure cristalline. Ce groupe comporte notamment un sous-groupe normal T composé des translations laissant le réseau invariant. Une maille primitive peut alors être vue comme un domaine fondamental du groupe T, c'est-à-dire la plus petite région reconstituant l'espace sous l'action de T. Une maille en général est un domaine fondamental d'un sous-groupe de T.

La notion de maille primitive peut être généralisée. On appelle unité asymétrique la plus petite région de l'espace qui, sous l'action de toutes les opérations du groupe d'espace G (pas seulement les translations comme pour la maille), permet de reconstruire la structure cristalline. On en déduit facilement que :

• les miroirs forment des faces de l'unité asymétrique ;
• les axes de rotations forment des arêtes de l'unité asymétrique ;
• les centres d'inversion sont, soit des sommets de l'unité asymétrique, soit positionnés au centre des faces ou des arêtes de l'unité asymétrique.

Ces restrictions ne s'appliquent pas aux axes hélicoïdaux et aux miroirs translatoires.

L'unité asymétrique correspond donc à la région fondamentale ou au domaine fondamental du groupe de symétrie du cristal. Ces termes seraient à préférer car une telle région n'est pas forcement dépourvue de symétrie mais peut avoir une forme régulière, en contradiction au moins apparente avec le terme d'unité asymétrique. Ce dernier terme est toutefois le terme standard retenu par l'Union internationale de cristallographie.

• Indices de Miller et indices de direction
• Réseau de Bravais

• [PDF] (en) Determination of Reduced Cells in Crystallography, A. D. Mighel, V. L. Karen, R. Munro