Algorithme LLL

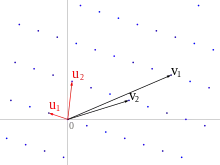
L'algorithme LLL procède à une réduction de base de réseau. Il prend en entrée un nombre d de vecteurs de base d'un réseau, tels que ces vecteurs soient de dimension n et de norme inférieure à B, et retourne en sortie une base de réseau LLL-réduite, c'est-à-dire presque orthogonale, en temps ${\displaystyle O(d^{5}n\log ^{3}B)\,}$.

L'algorithme LLL repose sur l'algorithme de réduction faible de bases, qui permet de rendre une base presque orthogonale.

Entrée : Une base ${\displaystyle B=(e_{1},...,e_{n})}$
Sortie : Une base réduite issue de ${\displaystyle B}$
LLL(B):
  B = ${\displaystyle (e_{1},...,e_{n})\leftarrow }$ ReducFaible(B)
  *On fait Gram-Schmidt*
  Pour i=1 à n :                      
     Pour j= 1 à i-1 :
        ${\displaystyle a_{i,j}\leftarrow {\dfrac {<e_{i},e_{j}>}{<e_{j},e_{j}>}}}$
      ${\displaystyle e_{i}\leftarrow e_{i}-\sum _{j<i}a_{i,j}e_{j}}$
  Si B est réduite
    retourne B
  Sinon
    ${\displaystyle i\leftarrow min(\lbrace ||j\in [1,n]~|~e_{j}+a_{j+1,j}e_{j+1}||^{2}<{\dfrac {3}{4}}||e_{j}||^{2}\rbrace )}$
    echanger(${\displaystyle e_{i}}$,${\displaystyle e_{i+1}}$)
    retourne LLL(B)

À l'origine, les applications consistaient en la production d'un algorithme de factorisation des polynômes à coefficients rationnels en produits de polynômes irréductibles, ainsi qu'en la résolution des problèmes d'optimisation linéaire avec solutions entières et dimensions fixes. D'autres applications ont été découvertes en cryptographie[1], notamment en cryptographie à clé publique, par exemple avec RSA, les cryptosystèmes basés sur le problème du sac à dos et NTRUEncrypt. En particulier l'algorithme LLL a rendu inefficaces tous les cryptosystèmes utilisant le problème du sac à dos[2]. Il sert également dans le cas des réseaux euclidiens.

• (en) A. Lenstra, H. Lenstra et L. Lovász, « Factoring polynomials with rational coefficients », Mathematische Annalen, vol. 261, n^o 4,‎ 1982, p. 515–534 (DOI 10.1007/BF01457454, MR 0682664, lire en ligne)
• (en) Peter Borwein, Computational Excursions in Analysis and Number Theory, Springer, 2002 (ISBN 978-0-387-95444-8) : contient une description complète de l'algorithmes ainsi que des implémentations en pseudocode
• Abuaf Roland, Boyer Ivan, « Factorisation dans ${\displaystyle \mathbb {Z} [X]}$ », Exposé de maîtrise proposé par François Loeser,‎ 20 juin 2007 (lire en ligne)