Liste des petits groupes
La liste mathématique suivante décrit les groupes finis (abéliens ou non abéliens) d'ordre inférieur ou égal à 20, à isomorphisme près.
Terminologie et notations
- Zn : le groupe cyclique d'ordre n (parfois noté Cn, il est isomorphe à Z/nZ).
- D2n : le groupe diédral d'ordre 2n.
- Sn : le groupe symétrique de degré n, contenant les n! permutations de n objets.
- An : le groupe alterné de degré n, contenant les n!/2 permutations paires de n objets.
- Dicn : le groupe dicyclique d'ordre 4n (généralisant les groupes de quaternions Q4n).
La notation G × H désigne le produit direct des deux groupes ; Gn désigne le produit direct de n copies du groupe G. G ⋊ H désigne un produit semi-direct où H agit sur G ; quand l'action exacte de H sur G est omise, toutes les actions non triviales conduisent au même groupe produit (à isomorphisme près).
Les groupes simples d'ordre n < 60 sont les groupes cycliques Zn, avec n premier. Le signe d'égalité ("=") désigne l'isomorphisme.
Dans les graphes des cycles, l'élément neutre est représenté par un cercle noir. Le plus petit groupe que ce graphe ne caractérise pas à isomorphisme près est d'ordre 16.
La liste des sous-groupes ne mentionne que ceux distincts du groupe trivial et du groupe entier. Quand il existe plusieurs sous-groupes isomorphes, leur nombre est indiqué entre parenthèses.
Petits groupes abéliens
Les groupes abéliens finis ont une classification simple : ils sont cycliques, ou produits directs de groupes cycliques.
| Ordre | Groupe | Sous-groupes | Propriétés | Graphe des cycles |
|---|---|---|---|---|
| 1 | groupe trivial = Z1 = S1 = A2 | - | de nombreuses propriétés triviales | |
| 2 | Z2 = S2 = D2 | - | simple, plus petit groupe non trivial | |
| 3 | Z3 = A3 | - | simple | |
| 4 | Z4 | Z2 | - | |
| groupe de Klein = Z2 × Z2 = D4 | Z2 (3) | plus petit groupe non cyclique | ||
| 5 | Z5 | - | simple | |
| 6 | Z6 = Z3 × Z2 | Z3 , Z2 | ||
| 7 | Z7 | - | simple | |
| 8 | Z8 | Z4 , Z2 | - | |
| Z4 × Z2 | Z22, Z4 (2), Z2 (3) | |||
| Z23 | Z22 (7) , Z2 (7) | les éléments autres que l'identité correspondent aux points du plan de Fano (le plus petit plan projectif fini), les Z2 × Z2 sous-groupes aux droites de ce plan | ||
| 9 | Z9 | Z3 | ||
| Z32 | Z3 (4) | |||
| 10 | Z10 = Z5 × Z2 | Z5 , Z2 | ||
| 11 | Z11 | - | simple | |
| 12 | Z12 = Z4 × Z3 | Z6 , Z4 , Z3 , Z2 | 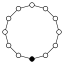 | |
| Z6 × Z2 = Z3 × Z22 | Z6 (3), Z3, Z2 (3), Z22 | 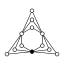 | ||
| 13 | Z13 | - | simple | 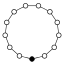 |
| 14 | Z14 = Z7 × Z2 | Z7 , Z2 | 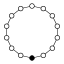 | |
| 15 | Z15 = Z5 × Z3 | Z5 , Z3 | 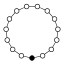 | |
| 16 | Z16 | Z8 , Z4 , Z2 | 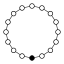 | |
| Z24 | Z2 (15) , Z22 (35) , Z23 (15) | 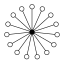 | ||
| Z4 × Z22 | Z2 (7) , Z4 (4) , Z22 (7) , Z23, Z4 ×Z2 (6) | ce groupe a le même graphe des cycles que celui engendré par les matrices de Pauli (mais ne lui est pas isomorphe) | 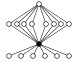 | |
| Z8 × Z2 | Z2 (3) , Z4 (2) , Z22, Z8 (2) , Z4 × Z2 | 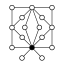 | ||
| Z42 | Z2 (3), Z4 (6) , Z22, Z4 × Z2 (3) | 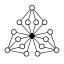 | ||
| 17 | Z17 | - | simple |
Petits groupes non abéliens
On ne connait pas de classification complète des groupes non abéliens. Tout groupe simple non abélien est d'ordre pair (c'est le théorème de Feit-Thompson) ; le plus petit est le groupe A5, d'ordre 60. Le plus petit groupe non abélien d'ordre impair est le groupe de Frobenius F21, d'ordre 21.
| Ordre | Groupe | Sous-groupes | Propriétés | Graphe des cycles |
|---|---|---|---|---|
| 6 | S3 = D6 | Z3 , Z2 (3) | plus petit groupe non abélien, groupe des symétries du triangle équilatéral | |
| 8 | D8 | Z4, Z22 (2) , Z2 (5) | groupe des symétries du carré | |
| groupe des quaternions = Q8 = Dic2 | Z4 (3), Z2 | plus petit groupe hamiltonien ; plus petit groupe admettant un groupe quotient non isomorphe à l'un de ses sous-groupes | ||
| 10 | D10 | Z5 , Z2 (5) | groupe des symétries du pentagone régulier | |
| 12 | D12 = D6 × Z2 | Z6 , D6 (2) , Z22 (3) , Z3 , Z2 (7) | groupe des symétries de l'hexagone régulier | 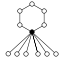 |
| A4 | Z22 , Z3 (4) , Z2 (3) | plus petit groupe n'admettant pas de sous-groupes de tous les ordres divisant l'ordre du groupe : pas de sous-groupe d'ordre 6 (voir le théorème de Lagrange et les théorèmes de Sylow) | 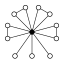 | |
| Dic3 = Z3⋊Z4 | Z2, Z3, Z4 (3), Z6 | 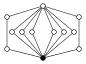 | ||
| 14 | D14 | Z7, Z2 (7) | groupe des symétries de l'heptagone régulier | 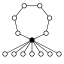 |
| 16[7] | D16 | Z8, D8 (2), Z22 (4), Z4, Z2 (9) | groupe des symétries de l'octogone régulier | 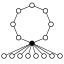 |
| D8 × Z2 | D8 (2), Z4 × Z2, Z23 (2), Z22 (11), Z4 (2), Z2 (11) | 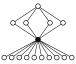 | ||
| groupe de quaternions généralisé Q16 = Dic4 | 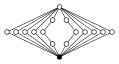 | |||
| Q8 × Z2 | groupe hamiltonien | 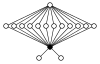 | ||
| Le groupe quasidiédral (en) d'ordre 16 | 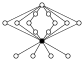 | |||
| Le groupe modulaire (en) d'ordre 16 |  | |||
| Z4⋊Z4 | 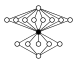 | |||
| Le groupe engendré par les matrices de Pauli | ce groupe a le même graphe des cycles que le groupe Z4 × Z22, mais ne lui est pas isomorphe |  | ||
| G4,4 = Z22⋊Z4 | 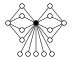 |
Notes et références
- Pour des ordres plus grands, voir la suite A000688 de l'OEIS.
- Pour des ordres plus grands, voir la suite
 A060689 de l'OEIS.
A060689 de l'OEIS. - (en) Marshall Hall, Jr., The Theory of Groups [détail des éditions], 1976, p. 52, aperçu sur Google Livres.
- Pour des ordres plus grands, voir la suite
 A000001 de l'OEIS.
A000001 de l'OEIS. - (en) « Groups of order 18 », sur groupprops.
- (en) « Groups of order 20 », sur groupprops.
- (en) Marcel Wild, « The Groups of Order Sixteen Made Easy », Amer. Math. Monthly, (lire en ligne)
Voir aussi
Article connexe
Liens externes
- Liste des groupes d'ordre inférieur ou égal à 31 dans : (en) Eric W. Weisstein, « Finite Group », sur MathWorld
- (en) Hans Ulrich Besche, Bettina Eick et Eamonn O'Brien, « The Small Groups library »