Plan de Fano
En géométrie projective finie, le plan de Fano, portant le nom du mathématicien Gino Fano, est le plus petit plan projectif fini, c'est-à-dire celui comportant le plus petit nombre de points et de droites, à savoir 7 de chaque. C'est le seul plan projectif (au sens des axiomes d'incidence) de 7 points, et c'est le plan projectif sur le corps fini à deux éléments.
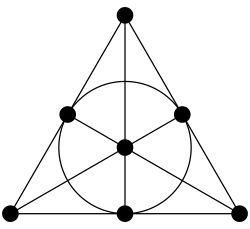
Deux définitions équivalentes
Le plan de Fano peut être défini de deux façons, soit comme le plan projectif sur le corps à deux éléments, soit comme le plus petit plan projectif vérifiant certains axiomes dits d'incidence. Ces derniers n'assurent pas a priori (c'est une particularité de la dimension 2) que le plan projectif est défini sur un corps, mais dans le cas du plan de Fano elles sont équivalentes : à isomorphisme près (bijection conservant l'alignement), il n'y a qu'un seul plan projectif d'ordre 2.
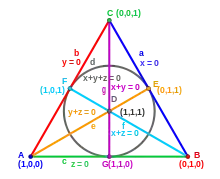
Définition algébrique
Le plan de Fano est le plan projectif sur le corps à deux éléments F2 = Z/2Z. Il est noté P2(F2), PG(2,F2)[1], ou simplement PG(2,2)[2]. Par définition les points du plan de Fano sont donc les droites vectorielles de l'espace vectoriel F23, chacune de ces droites possède deux éléments dont un seul est non nul, et qui définit donc le point. Le plan de Fano possède donc exactement 23 – 1 = 7 points (les 7 éléments non nuls de F23). Les droites (projectives) du plan de Fano sont les plans vectoriels de F23, définis par une équation ax + by + cz = 0, où les coefficients a, b et c sont 0 ou 1, et non tous nuls, ce qui fait également 7 droites.
La dualité entre l'espace vectoriel F23 et l'espace dual de ses formes linéaires induit une correspondance bijective par dualité entre points et droites[3] du plan projectif. Une telle correspondance (elle n'est pas unique) est indiquée sur le dessin ci-contre.
Le plan de Fano défini comme structure d'incidence
Une structure d'incidence est la donnée de deux ensembles P (les éléments de P sont appelés points) et D (les éléments de D sont appelés droites) disjoints et d'une relation binaire I entre éléments de P et éléments de D, soit un sous-ensemble de P×D. Dans ce cadre, un plan projectif est alors défini comme une structure d'incidence vérifiant les axiomes d'incidence de la géométrie projective plane[4]. Pour « un point et une droite sont incidents », on dit également que le point est sur la droite ou que la droite passe par le point.
Ainsi le plan projectif PG(2,F2) définit bien une structure d'incidence, qui peut se décrire soit par la matrice de la relation binaire, dite matrice d'incidence, ou par la donnée pour chaque droite des ensembles de points qui lui sont incidents. Pour les notations du dessin ci-dessus, cela donne (la matrice ci-dessous répond à la question « telle droite est-elle incidente à tel point ? », 1 signifiant que oui, et 0 que non) :
|
|
Si l'on voit chacune des 7 droites comme l'ensemble des 3 points qui lui sont incidents, la relation d'incidence est la relation d'appartenance à cet ensemble. Mais on pourrait tout aussi bien donner pour chaque point l'ensemble des droites passant par ce point. Deux points X et Y étant donnés, l'unique droite passant par X et Y peut se noter (XY). Deux droites distinctes x et y étant données, l'unique point à l'intersection de x et y peut se noter x ∩ y[5]. La symétrie de la matrice met en évidence une correspondance par dualité entre points et droites : on peut échanger les noms des points et des droites et l'on obtient la même matrice. Une matrice d'incidence du plan de Fano n'est pas nécessairement symétrique[6].

On vérifie qu'un plan projectif défini axiomatiquement par les seuls axiomes d'incidence contient au moins 7 points et 7 droites. En effet les axiomes d'incidence imposent l'existence d'un quadrangle, c'est-à-dire d'un quadrilatère dont 3 points parmi ces 4 ne sont jamais alignés et qui définit donc 6 droites distinctes. On note (ABCD) le quadrangle. Chacun des trois points diagonaux, E = (AD)∩(BC), F =(BD)∩(CA) et G = (CD)∩(AB) ne peut être situé sur aucune autre droite que les deux qui le définissent, car sinon deux des 6 droites initiales seraient confondues. En particulier les 3 points diagonaux ne peuvent être confondus ni entre eux, ni avec les points de départ, et donc le plan possède 7 points au moins. On peut décider que les 3 points diagonaux sont alignés, on obtient ainsi une structure d'incidence de 7 points et 7 droites dont on vérifie facilement qu'elle satisfait les axiomes de plan projectif. La structure est en fait identique à celle définie algébriquement précédemment. Tout autre choix indurait l'existence de 3 nouvelles droites (EF), (FG) et (EG), et par intersection par exemple de (EF) avec (CD), de nouveaux points. Il n'y a donc, à isomorphisme de la structure d'incidence près, qu'un seul plan de 7 points qui est bien le plus petit plan projectif défini par les axiomes d'incidences[7].
Qui plus est dans le plan de Fano, tout quadrangle complet a ses 3 points-diagonaux alignés. On en déduit la propriété duale, à savoir que dans le plan de Fano, tout quadrilatère complet, donnée de 4 droites dont aucune combinaison de 3 n'est concourante, a ses 3 diagonales concourantes.
Configuration de Fano dans un plan projectif
Ces propriétés sont le cas particulier d'un résultat plus général. On appelle configuration de Fano la donnée dans un plan projectif d'un quadrangle complet dont les points diagonaux sont alignés. Alors[8] :
Proposition. — Soit E un espace vectoriel de dimension 3 sur un corps K. Si le plan projectif P(E) contient une configuration de Fano, le corps K est de caractéristique 2, et alors tout quadrangle complet a ses points diagonaux alignés. Réciproquement si le corps est de caractéristique 2, tous les quadrangles complets sont des configurations de Fano.
En particulier il n'est pas possible de plonger le plan de Fano dans le plan projectif réel (caractéristique 0), et donc dans le plan euclidien usuel, en conservant l'alignement de tous les points : dans toutes les représentations du plan de Fano au moins l'une des droites est représentée par une courbe.
La proposition peut se démontrer en se ramenant à la géométrie affine. Si l'on rejette à l'infini les deux points diagonaux E et G, le quadrangle (ABCD) devient un parallélogramme. Dire que les points E, F et G sont alignés, se traduit alors par le fait que le point F est à l'infini, c'est-à-dire que les diagonales (AC) et (BD) sont parallèles. Un simple calcul vectoriel permet de vérifier que c'est bien le cas si le corps est de caractéristique 2, et que sinon, c'est-à-dire dès que l'on peut diviser par 2 dans le corps et donc parler de milieu de deux points, ça n'est pas possible.
Par dualité on a le résultat analogue pour les quadrilatères complets.
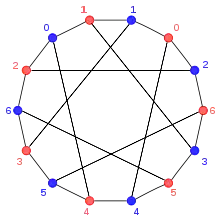
Ensemble parfait de différences
Une conséquence immédiate de la définition comme structure d'incidence est qu'un plan projectif fini peut être vu comme un graphe biparti, points et droites. Celui du plan de Fano est le graphe de Heawood[9].
À la permutation circulaire x ↦ x + 1 modulo 7 correspond une collinéation du plan, la permutation des droites associée correspondant à x ↦ x - 1 modulo 7.
L'indexation des points des droites du plan de Fano fournie par le graphe de Heawood permet de caractériser arithmétiquement la relation d'incidence, en utilisant la congruence modulo 7. Les éléments de Z/7Z peuvent être représentés par les restes par la division par 7, soit {0, 1, 2, 3, 4, 5, 6}.
- points: 0, 1, 2, 3, 4, 5, 6
- droites : {0, 1, 3}, {1, 2, 4}, {2, 3, 5}, {3, 4, 6}, {4, 5, 0}, {5, 6, 1}, {6, 0, 2}
Il y a 7 points et 7 droites. Suivant le graphe, les droites sont obtenues successivement à partir de la première ({0, 1, 3}) et en ajoutant le même entier à chacun des éléments de la première droite. La numérotation des droites se déduit par symétrie de celle des points.
On en déduit que le sous-ensemble {0, 1, 3} est un ensemble parfait de différences de Z/7Z, ce qui signifie que tout élément de Z/7Z s'écrit comme différence (prise modulo 7) de deux éléments de ce sous-ensemble[10].
| 0 | 1 | 3 | 3 | 0 | 1 | 0 |
| − 0 | − 0 | − 1 | − 0 | − 3 | − 3 | − 1 |
| = 0 | = 1 | = 2 | = 3 | = 4 | = 5 | = 6 |
L'indexation des points et des droites fournit la caractérisation arithmétique suivante. Un point est incident à une droite quand la somme modulo 7 des indices du point et de la droite appartient à l'ensemble parfait de différences {0, 1, 3}, il n'est pas incident dans le cas contraire.
À l'application sur Z/7Z est donc associée par cette indexation une permutation des points du plan qui préserve l'alignement (que l'on appelle collinéation (en)), et qui engendre un groupe cyclique à 7 éléments. L'orbite d'un point du plan est l'ensemble de tous les points du plan ; de même pour les droites.
Plan de Fano et groupe multiplicatif du corps fini F8
Si on voit maintenant F23 comme le corps fini F8 (qui a une structure d'espace vectoriel de dimension 3 sur F2) les points du plan de Fano correspondent aux éléments de F8*, groupe multiplicatif de F8 ; celui-ci est cyclique, donc isomorphe au groupe additif Z/7Z et engendré par un élément primitif α (voir l'article « Corps fini »). Tout élément du plan de Fano est une puissance de α, et (1, α, α2) est une base de l'espace vectoriel F8. La multiplication par α définit une application linéaire bijective sur F8, donc une homographie de l'espace projectif. À αi elle associe αi+1, et en indexant αi par i, on retrouve la collinéation du précédent paragraphe : une droite projective définit alors un ensemble parfait de différences. En utilisant cette méthode, ce résultat se généralise alors à n'importe quel plan projectif sur un corps fini[11].
Groupe des symétries
Une permutation des sept points du plan de Fano qui conserve l'alignement est appelée collinéation (en), automorphisme ou symétrie du plan. Ces permutations forment un groupe. Dans le cas du plan de Fano, défini sur un corps premier, les collinéations sont toutes des homographies, et le corps n'ayant que deux éléments, ces homographies sont déterminées de façon unique par l'application linéaire sur F23 associée, c'est-à-dire par une matrice inversible 3x3 à coefficients dans F2. Il y a 7×6×4 = 168 telles matrices, toutes de déterminant 1. Le groupe des symétries du plan de Fano est donc le groupe général linéaire GL(3,2) mais aussi le groupe spécial linéaire PSL(3,2), et on peut montrer que c'est l'unique groupe simple d'ordre 168, qui est encore le groupe projectif spécial linéaire PSL(2,7)[12].
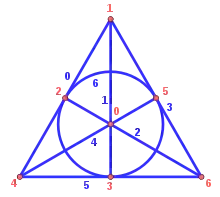
Ce groupe se décompose en 6 classes de conjugaison, qui peuvent être décrites en termes de permutations des points. Ceux-ci sont numérotés comme sur le schéma de la section précédente, le point 0 étant renommé 7.
 l'identité ;
l'identité ; 21 permutations d'ordre 2 conjuguées de (25)(46), les 3 points fixes étant alignés, et pour l'un des points fixes, les 2 autres droites passant par ce point étant globalement invariantes, c'est-à-dire que la permutation échange 2 à 2 les deux autres points de chacune de ces 2 droites ;
21 permutations d'ordre 2 conjuguées de (25)(46), les 3 points fixes étant alignés, et pour l'un des points fixes, les 2 autres droites passant par ce point étant globalement invariantes, c'est-à-dire que la permutation échange 2 à 2 les deux autres points de chacune de ces 2 droites ; 56 permutations d'ordre 3 conjuguées de (267)(346), définies par un point fixe, une droite ne passant pas par ce point et une permutation circulaire des 3 points de cette droite, la permutation circulaire des 3 autres points non alignés étant alors déduite par alignement ;
56 permutations d'ordre 3 conjuguées de (267)(346), définies par un point fixe, une droite ne passant pas par ce point et une permutation circulaire des 3 points de cette droite, la permutation circulaire des 3 autres points non alignés étant alors déduite par alignement ; 42 permutations d'ordre 4 conjuguées de (37)(2546), une droite passant par le point fixe voit ses deux autres points échangés par la permutation, la permutation circulaire des 4 points restants étant choisie de façon que le point fixe un point et son image ne soient pas alignés ;
42 permutations d'ordre 4 conjuguées de (37)(2546), une droite passant par le point fixe voit ses deux autres points échangés par la permutation, la permutation circulaire des 4 points restants étant choisie de façon que le point fixe un point et son image ne soient pas alignés ;- deux classes de 24 cycles d'ordre 7
 24 permutations conjuguées de (1234567), on peut nommer les 7 points A, B, C, D, ... de façon que A a pour image B, B a pour image C non aligné avec A et B, C a pour image le 3e point sur AB, D le 3e point sur BC, etc. ;
24 permutations conjuguées de (1234567), on peut nommer les 7 points A, B, C, D, ... de façon que A a pour image B, B a pour image C non aligné avec A et B, C a pour image le 3e point sur AB, D le 3e point sur BC, etc. ; 24 permutations conjuguées de (1237645), A a pour image B, B a pour image C non aligné avec A et B, C a pour image le 3e point sur AC, D le 3e point sur BD, etc.
24 permutations conjuguées de (1237645), A a pour image B, B a pour image C non aligné avec A et B, C a pour image le 3e point sur AC, D le 3e point sur BD, etc.
D'après le théorème de dénombrement de Pólya, le nombre de façons non équivalentes de colorer le plan de Fano avec n couleurs est par conséquent :
Voir aussi
Notes et références
- Par exemple Casse 2006, p. 49.
- PG pour projective geometry, le premier argument est la dimension de l'espace, le second le nombre d'éléments du corps fini, notation due à Oswald Veblen et W. H. Bussey, voir Coxeter 1987, p. 91.
- Lelong-Ferrand 1985, p. 133.
- Définition non équivalente à la précédente dans le cas général ; Lelong-Ferrand 1985, p. 161, parle de plan de type projectif, mais souligne que le plus souvent on parle également de plan projectif.
- Notations de Lelong-Ferrand 1985, on trouve aussi, par exemple, XY et x•y : Coxeter 1987, p. 7, et d'autres.
- il suffit ci-dessus d'échanger deux noms de droites, les points restant dans le même ordre, pour s'en convaincre.
- Lelong-Ferrand 1985, p. 162.
- Lelong-Ferrand 1985, p. 142.
- Coxeter 1950, p. 424.
- Coxeter 1987, p. 93, le plan de Fano est traité en exercice page 96.
- C'est le théorème de Singer : voir Casse 2006, p. 70 ; à noter que dans le cas général, PG(2,Fq) ne s'identifie plus au groupe multiplicatif (Fq3)*, mais à son quotient par Fq*.
- (en) E. Brown et N. Loehr, « Why is PSL(2,7)≅GL(3,2)? », The American Mathematical Monthly, vol. 116, no 8, , p. 727-732 (DOI 10.4169/193009709X460859)
Bibliographie
- (en) H. S. M. Coxeter, Projective Geometry, Springer Verlag, , 2e éd., 162 p. (ISBN 0-387-40623-9, lire en ligne).
- (en) H. S. M. Coxeter, « Self-dual configurations and regular graphs », Bull. Amer. Math. Soc., vol. 56, (lire en ligne), plus particulièrement pages 423-425.
- Jacqueline Lelong-Ferrand, Fondements de la géométrie, Paris, PUF, , 287 p. (ISBN 2-13-038851-5)
- (en) Rey Casse, Projective Geometry : An Introduction, Oxford University Press, , 198 p. (ISBN 0-19-929885-8, lire en ligne).

