Octonion

L'espace 𝕆 des octonions est un espace vectoriel réel de dimension 8 rapporté à une base notée (1, i, j, k, l, il, jl, kl) (en anticipant légèrement la définition de la multiplication).

Autrement dit : chaque octonion x s'écrit de manière unique comme combinaison linéaire à coefficients réels x_n de ces huit éléments :

${\displaystyle x=x_{0}+x_{1}{\rm {i}}+x_{2}{\rm {j}}+x_{3}{\rm {k}}+x_{4}{\rm {l}}+x_{5}{\rm {il}}+x_{6}{\rm {jl}}+x_{7}{\rm {kl}}}$

et les deux opérations d'espace vectoriel (addition de deux octonions et multiplication à gauche d'un octonion par un réel) se font coordonnée par coordonnée.

La multiplication des octonions est alors définie comme l'unique application bilinéaire, c'est-à-dire vérifiant

${\displaystyle \forall a,b,c\in \mathbb {O} ,\forall \lambda \in \mathbb {R} ,\qquad \left\{{\begin{matrix}(a+b)c=ac+bc\\a(b+c)=ab+ac\\(\lambda a)b=a(\lambda b)=\lambda (ab)\end{matrix}}\right.}$

et dont les valeurs sur les vecteurs de base sont données par la table de multiplication ci-dessous :

On remarque immédiatement que :

• (cases blanches) 1 est neutre (premières ligne et colonne de la table) et les 7 autres éléments de la base ont pour carré –1 (diagonale) ;
• (cases vertes) deux éléments distincts a et b, parmi les 7 éléments de la base différents de 1, anticommutent (ab = –ba) (hormis dans les lignes et colonnes 1 et sur la diagonale où le produit est commutatif, la table est antisymétrique en signe par rapport à la diagonale).
• Le quart supérieur gauche de la table est identique à la table de la multiplication des quaternions. En particulier : ij = k, jk = i, ki = j.

Le choix initial de (1, i, j, k, l, il, jl, kl) comme base est bien sûr arbitraire : comme on le verra plus loin, il y a bien d'autres choix pour i et j tels que, en posant k = ij et en choisissant l convenablement, on obtienne la même table. Par ailleurs, étant donné un tel choix, une autre base est par exemple (1, i, j, k, l, li, lj, lk) : la table est alors modifiée par des changements de signes.

Plan mnémotechnique de Fano

La même figure gravée sur une boule de pétanque

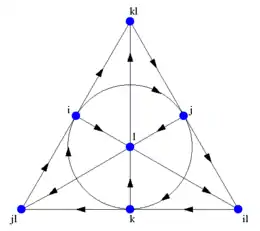
Un moyen mnémotechnique pour se rappeler les produits des octonions unitaires est donné par le diagramme ci-contre.

Ce diagramme à sept points et sept « cercles » (sur la figure plane, les segments joignant 3 points sont considérés comme des cercles en les prolongeant à l'infini de chaque côté où ils se rejoignent) est appelé le plan de Fano (il s'agit en fait du plan projectif construit sur le corps à deux éléments Z/2Z). Les cercles sont orientés dans ce diagramme. Les sept points correspondent aux sept éléments non réels de la base de 𝕆. Chaque paire de points se trouve sur un cercle unique, et chaque cercle traverse exactement trois points.

La même figure peut aussi être retracée (ou imaginée tracée) pour la plaquer sur une sphère où les 7 cercles seront plus évidents (tels les cercles gravés sur une boule de pétanque). Dans le plan de Fano toutefois, les cercles sont désignés comme des « droites ».

Soit (a, b, c) un triplet ordonné de points situés sur un des cercles donné avec l’ordre donné par la direction de la flèche. La multiplication est donnée par :

• ab = c, ba = –c

avec des permutations circulaires conservant l'ordre relatif donné par la direction du cercle :

• bc = a, cb = –a
• ca = b, ac = –b

Les multiplications opèrent avec la huitième dimension (réelle) de la manière suivante :

• 1 est l’élément neutre pour la multiplication,
• e² = –1 pour chaque point e du diagramme définit complètement la structure algébrique des octonions.

Chacun des sept cercles engendre une sous-algèbre de 𝕆 isomorphe aux quaternions ℍ.

Le conjugué d'un octonion

${\displaystyle x=x_{0}+x_{1}{\rm {i}}+x_{2}{\rm {j}}+x_{3}{\rm {k}}+x_{4}{\rm {l}}+x_{5}{\rm {il}}+x_{6}{\rm {jl}}+x_{7}{\rm {kl}}}$

est donné par

${\displaystyle x^{*}=x_{0}-x_{1}{\rm {i}}-x_{2}{\rm {j}}-x_{3}{\rm {k}}-x_{4}{\rm {l}}-x_{5}{\rm {il}}-x_{6}{\rm {jl}}-x_{7}{\rm {kl}}.}$

La conjugaison est une involution de 𝕆 et satisfait

${\displaystyle (xy)^{*}=(y^{*})(x^{*})}$

(noter le changement dans l’ordre de succession).

La partie réelle de l’octonion x est définie comme suit

• ${\displaystyle {\rm {Re}}(x)={\frac {x+x^{*}}{2}}=x_{0}}$

et sa partie imaginaire

• ${\displaystyle {\rm {Im}}(x)={\frac {x-x^{*}}{2}}=x_{1}{\rm {i}}+x_{2}{\rm {j}}+x_{3}{\rm {k}}+x_{4}{\rm {l}}+x_{5}{\rm {il}}+x_{6}{\rm {jl}}+x_{7}{\rm {kl}}}$

de sorte que pour tout octonion x,

• ${\displaystyle {\rm {Re}}(x)+{\rm {Im}}(x)=x,}$
• ${\displaystyle {\rm {Re}}(x^{*})={\rm {Re}}(x),}$
• ${\displaystyle {\rm {Im}}(x^{*})=-{\rm {Im}}(x).}$

L’ensemble de tous les octonions purement imaginaires (dont la partie réelle est nulle) forme un ℝ-sous-espace vectoriel de 𝕆 de dimension 7, donc isomorphe à ℝ⁷. Ce n'est pas une sous-algèbre : par exemple, le carré d'un octonion purement imaginaire non nul est un réel strictement négatif.

L’ensemble de tous les octonions purement réels (dont la partie imaginaire est nulle) forme une sous-algèbre à une dimension de 𝕆, isomorphe à ℝ.

La norme d’un octonion x est définie comme la racine carrée d'un nombre réel positif :

• ${\displaystyle \|x\|\ =\ {\sqrt {x\ \ x^{*}}}={\sqrt {x_{0}^{2}+x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+x_{4}^{2}+x_{5}^{2}+x_{6}^{2}+x_{7}^{2}}}}$.

Cette norme correspond à la norme euclidienne sur ℝ⁸.

${\displaystyle \|x\|^{2}=[{\rm {Re}}(x)]^{2}-[{\rm {Im}}(x)]^{2}}$.

L’existence d’une norme sur 𝕆 implique l’existence d’un inverse pour chaque élément non nul dans 𝕆. L’inverse de tout x non nul est donné par :

${\displaystyle x^{-1}\ =\ \|x\|^{-2}\ x^{*}.}$

À l’instar des quaternions assimilés aux couples de nombres complexes (et des nombres complexes assimilés aux couples de nombres réels), les octonions peuvent être traités sous forme de couples de quaternions.

Le ℝ-espace vectoriel produit ℍ × ℍ des couples de quaternions est par construction isomorphe à 𝕆, via l'application (définie en identifiant naturellement ℍ à une sous-algèbre de 𝕆) :

${\displaystyle \mathbb {H} ^{2}\to \mathbb {O} ,\quad (c,d)\mapsto c+d~{\rm {l}}.}$

Via cet isomorphisme, la multiplication dans 𝕆 se transcrit dans ℍ × ℍ en[1] :

${\displaystyle (a,b)\times (c,d)=(ac-d^{*}b,da+bc^{*})}$

où z* désigne le conjugué du quaternion z.

L'espace ℍ², muni de cette multiplication, forme donc une ℝ-algèbre isomorphe à 𝕆 (attention : 𝕆 n'est pas une ℍ-algèbre ni même un ℂ-espace vectoriel).

La construction de Cayley-Dickson rend fastidieuse la vérification de certaines propriétés des octonions de la base canonique, notamment de symétrie, anti-commutativité et anti-associativité : par exemple, a, b, c étant des éléments de base, trouver le signe correct dans (ab)c = +/– a(bc) nécessite à priori 512 = 8³ calculs. Une construction des octonions basée sur le corps à 8 éléments permet de remédier à cette difficulté. Elle nécessite des connaissances minimales sur les corps finis.

Un automorphisme de l'algèbre des octonions est un automorphisme d'espace vectoriel A de 𝕆 qui vérifie de plus

${\displaystyle A(xy)=A(x)A(y).}$

Le groupe des automorphismes de 𝕆 est le groupe G₂. C'est un groupe de Lie réel simplement connexe et compact, de dimension 14. Ce groupe est le plus petit des cinq groupes de Lie exceptionnels.

• Identité des huit carrés de Degen
• Produit vectoriel en dimension 7
• Nombre hypercomplexe
  • Quaternion
  • Biquaternion
  • Coquaternion
  • Octonion déployé
  • Sédénion
• Algèbre à division
• Corps non commutatif

• (en) John C. Baez, « The Octonions », Bull. Amer. Math. Soc., vol. 39,‎ 2002, p. 145-205 (lire en ligne)
• Images fractales octonioniques réalisées avec Gecif à partir des octonions
• Octavions, Dictionnaire des nombres, Gérard Villemin