Structure algébrique
En mathématiques, une structure algébrique est définie axiomatiquement par une ou plusieurs opérations sur un ensemble (dites internes), éventuellement muni d’autres opérations (externes) dépendant d’autres ensembles, toutes ces opérations satisfaisant certaines relations telles que l’associativité, la commutativité ou la distributivité.
La structure de groupe qui émerge progressivement au XIXe siècle, avec une seule opération interne et quelques propriétés se formalise au début du XXe siècle avec une kyrielle de structures d’algèbre générale moins restrictives (monoïde) ou au contraire enrichies par une seconde opération (anneau, corps, algèbre de Boole…) voire par l’action d’une autre structure (module sur un anneau, espace vectoriel, algèbre sur un corps…) ou encore une relation d'ordre, une topologie…
Les applications compatibles avec les opérations entre deux ensembles présentant la même structure sont appelés morphismes et permettent de formuler cette structure dans le contexte de la théorie des catégories.
Dans le contexte de l’algèbre universelle, la notion de structure algébrique est un peu différente et ne s’applique pas aux structures de corps, mais permet de décrire certaines structures topologiques.
Avec une seule loi interne
Beaucoup d’opérations binaires classiques peuvent être considérées comme des lois de composition internes, c’est-à-dire que le résultat est toujours bien défini dans le même ensemble que les opérandes : addition, soustraction et multiplication des entiers relatifs voire des rationnels ou des réels, exponentiation sur les entiers naturels, concaténation des mots, intersection et réunion de parties d’un ensemble, ET et OU logiques… Sans plus d’hypothèses, une telle opération définit un magma (ou groupoïde, mais ce terme est repris dans un sens différent en théorie des catégories) et s’écrit en général multiplicativement : le résultat de l’opération appliquée à x et y se note xy ou x∗y (le symbole ∗ pouvant être remplacé par n’importe quel autre qui se distingue de ceux qui désignent les éléments de l’ensemble).
Propriétés supplémentaires
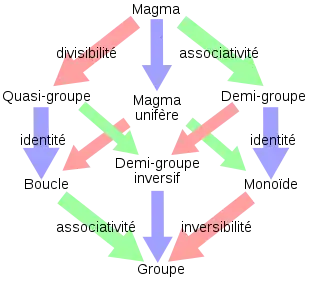
Associativité
Si le résultat est à nouveau utilisé avec un troisième élément, il faut a priori spécifier avec des parenthèses l’ordre de calcul : (x∗y)∗z n’est pas forcément égal à x∗(y∗z). C’est souvent le cas par exemple avec la soustraction ou l’exponentiation : (3 − 2) − 1 ≠ 3 − (2 − 1) et (31)2 ≠ 3(12).
La propriété d’associativité permet de supprimer cette ambiguïté lorsqu’on compose plus de deux opérations enchainées : on note alors indifféremment x∗y∗z pour (x∗y)∗z = x∗(y∗z). Un magma associatif est appelé demi-groupe.
Régularité
Une autre propriété utile est la régularité, qui permet de transformer l’égalité x∗y = x∗z en y = z et x∗z = y∗z en x = y. Autrement dit, tous les éléments sont simplifiables à gauche et à droite. C’est bien le cas pour la soustraction des nombres ou la concaténation des mots, mais pas pour la multiplication (on ne peut pas simplifier la multiplication par zéro).
Une propriété plus forte est l’existence d’une unique solution à chaque équation de la forme a∗x = y ou x∗b = z d’inconnue x. Cela signifie alors que chaque élément apparaît une et une seule fois dans chaque ligne et chaque colonne de la table de la loi. Un magma qui satisfait cette propriété est un quasigroupe.
Neutre
Un élément e est neutre (à gauche et à droite) s’il vérifie pour tout élément x de l’ensemble e∗x = x = x∗e. C’est le cas par exemple de zéro pour l’addition, de 1 pour la multiplication, de l’ensemble vide pour la réunion… Pour l’exponentiation, le nombre 1 est un neutre à droite (x1 = x) mais il n’en existe pas à gauche. Un magma qui possède un neutre est dit unifère. Un demi-groupe unifère est un monoïde. Un quasigroupe unifère est une boucle.
Dès lors que les trois propriétés sont vérifiées (associativité, simplifiabilité et existence d’un neutre), la structure obtenue est un groupe, avec de nombreux exemples en théorie des nombres (addition des entiers relatifs, multiplication des réels non nuls), en géométrie (isométries de figures du plan ou de l’espace, groupes de frises ou de pavages), en combinatoire (groupe de permutations), en topologie (groupe de tresses)…
Commutativité
La loi est dite commutative lorsque le résultat ne dépend pas de l’ordre des opérandes : x∗y = y∗x. C’est le cas de l’addition, de la multiplication ou de la distance entre deux nombres (d(x, y) = |x−y| = |y−x|), mais pas de la soustraction, de la concaténation de mots ou du produit matriciel.
Un groupe commutatif est appelé spécifiquement groupe abélien.
Morphismes et sous-structures
Un morphisme entre deux magmas f : M → N est une application qui compatible avec la loi de composition interne : f(x∗y) = f(x)∗f(y).
Les hypothèses d’associativité ou de régularité ne changent rien à cette définition. En outre, l’image du neutre de M (s’il existe) est bien neutre dans f(M) mais pas forcément neutre dans N (même s’il existe), sauf si N est un quasigroupe (a fortiori si c’est un groupe).
Un sous-magma de M est une partie A stable par la loi de composition, c’est-à-dire que quels que soient x, y dans A, on a x∗y ∈ A. Dans ce cas, A est associatif ou régulier si M l’était déjà.
Avec deux lois de composition internes
Ces structures comportent deux lois de composition internes. Il est d’usage courant de qualifier d’additive la première loi et de multiplicative la seconde. Autrement dit, la première loi est nommée addition (souvent notée ⊕ pour la distinguer de l’addition usuelle) et la seconde est nommée multiplication ou produit (souvent notée ⊗). La seconde loi est distributive bilatéralement (c’est-à-dire à gauche et à droite) par rapport à la première loi.
- Anneau non associatif (en) : un ensemble muni d’une structure de groupe abélien pour l’addition (qui est donc associative et commutative), la multiplication ne vérifiant a priori que la distributivité sur l’addition[1].
- Pseudo-anneau : un anneau non associatif dont la multiplication est en outre associative (structure de demi-groupe sur la multiplication).
- Demi-anneau : un ensemble muni de deux structures de monoïde et où la multiplication est distributive par rapport à l’addition et où l’élément neutre de l’addition est absorbant pour la multiplication[2]. Un demi-anneau est aussi appelé « semi-anneau ».
- Dioïde : un demi-anneau dans lequel le préordre défini par l’addition est une relation d'ordre.
- Anneau (unitaire) : un pseudo-anneau dont la loi multiplicative est en outre unifère (c’est donc un monoïde pour la multiplication). C’est encore un demi-anneau où l’addition crée une structure de groupe abélien. Certains auteurs appellent « anneau » ce que l’on a appelé « pseudo-anneau » ci-dessus et appellent « anneau unitaire » ce que l’on a appelé « anneau » ici.
- Anneau commutatif : un anneau dont la multiplication est en outre commutative.
- Anneau intègre : un anneau commutatif non nul et sans diviseur de zéro, c’est-à-dire que tout élément non nul de l’anneau est régulier pour la multiplication.
- Corps : un anneau où l’élément neutre de l’addition n’est pas celui de la multiplication et où tout élément non nul a un inverse multiplicatif. À cause de l’influence anglaise (voir ci-dessous), un corps est souvent considéré comme implicitement commutatif, alors que dans la tradition française, il ne l’est pas nécessairement. Pour éviter toute ambiguïté, il vaut mieux indiquer :
- « corps commutatif » pour un corps effectivement commutatif,
- « corps gauche » pour un corps « en principe » non commutatif,
- « corps commutatif ou non », ou « corps quelconque », pour un corps non nécessairement commutatif.
Structures à opérateurs externes
Ces structures peuvent être considérées d’un point de vue algébrique ou géométrique.
Algébriquement, une structure externe est un ensemble muni d’une loi de composition externe sur une structure de base, et éventuellement d’une ou plusieurs lois de composition interne.
Géométriquement, c’est un ensemble E sur lequel agit un ensemble-opérateur S, encore appelé ensemble des opérateurs ou scalaires. Pour cela, l'ensemble E est muni d’une action, c’est-à-dire d’une application de S dans EE (ensemble des transformations de E, c'est-à-dire des applications de E dans E).
La correspondance entre les actions et les lois externes est bijective ; c’est pourquoi les lois externes sont souvent appelées lois d’action.
Espaces homogènes
Ces structures ne comportent qu'une seule loi, qui est externe, un exemple est :
- Espace homogène : ensemble sur lequel un groupe G opère transitivement,
Moduloïdes
Structures possédant à la fois une loi de composition interne et une loi de composition externe.
- Groupe à opérateurs (dans un ensemble) : groupe muni d’une loi externe sur un ensemble d’opérateurs, distributive par rapport à la loi du groupe
- Module sur un anneau, on distingue les modules à gauche et à droite sur un anneau non commutatif.
- Espace vectoriel (sur un corps) : module sur un corps K, on doit distinguer également les espaces vectoriels à gauche et à droite si le corps n'est pas commutatif.
- Espace affine (sur un corps) : espace homogène d'un espace vectoriel sur un corps K.
Algèbres
Structures possédant deux lois internes et une loi externe.
- Algèbre (sur un anneau commutatif) : un module (ou un espace vectoriel) muni en plus d’une loi de composition interne bilinéaire.
- Algèbre associative : une algèbre (sur un anneau commutatif) dont la multiplication est associative.
- Algèbre sur un corps : une algèbre sur un anneau commutatif qui, lui, est un corps.
- Algèbre associative sur un corps : à la fois une algèbre associative et une algèbre sur un corps.
- Algèbre unitaire : une algèbre ayant un élément neutre pour la multiplication.
- Algèbre commutative : une algèbre dont la multiplication est commutative.
- Algèbre de Lie : un type particulier d’algèbre généralement non associative, importante dans l'étude des groupes de Lie.
- Algèbre de Jordan : un type particulier d’algèbre généralement non associative.
Bialgèbres
Structures possédant deux lois internes, une loi externe, et une loi "duale" de l'une des deux lois internes.
Structures algébriques ordonnées
Groupes ordonnés et anneaux ordonnés
On s'intéresse ici aux structures algébriques compatibles avec une relation d'ordre.
- Un monoïde ordonné est un monoïde commutatif muni d'une relation d'ordre compatible avec l'opération, c'est-à-dire telle que implique pour tout . On définit de même un monoïde préordonné en remplaçant la relation d'ordre par une relation de préordre.
- Un groupe ordonné est un monoïde ordonné qui est un groupe commutatif. Un groupe préordonné est un monoïde préordonné qui est un groupe.
- Un anneau ordonné est un anneau commutatif muni d'une relation d'ordre pour laquelle il est groupe ordonné pour l'addition et tel que le produit de deux éléments supérieurs ou égaux à 0 sont supérieurs ou égaux à 0.
- Un corps ordonné est un anneau ordonné qui est un corps.
Treillis
Ensembles munis de deux lois internes, qui peuvent aussi s’interpréter comme la borne supérieure et la borne inférieure des couples au sens des relations d'ordre.
- Treillis : un ensemble muni de deux lois de composition internes commutatives, associatives et idempotentes satisfaisant la loi d’absorption.
- Algèbre de Boole : un treillis borné, distributif et complémenté.
Structures algébriques topologiques
Structures et topologies, distances, normes ou produits scalaires
Les structures algébriques peuvent également posséder des caractéristiques additionnelles topologiques.

Ainsi, en allant du général au particulier (topologie > distance > norme > produit scalaire) :
- Une structure algébrique peut être munie d'une topologie, devenant ainsi un espace topologique pour lequel chacune de ses lois externes et internes sont continues.
- Un semi-groupe topologique est un demi-groupe muni d'une topologie rendant continue sa loi de composition interne.
- Un monoïde topologique est un demi-groupe topologique unifère. C'est aussi un monoïde muni d'une topologie rendant continue sa loi de composition interne.
- Un groupe topologique est un groupe muni d'une topologie rendant continue sa loi de composition interne, ainsi que l'application qui à tout élément du groupe associe son inverse.
- Un anneau topologique est un anneau muni d'une topologie pour laquelle le groupe additif sous-jacent est un groupe topologique et le monoïde multiplicatif sous-jacent est un monoïde topologique.
- Un corps topologique est un corps muni d'une topologie qui en fait un anneau topologique et pour laquelle le groupe multiplicatif des éléments non nuls est un groupe topologique.
- Un corps valué est un corps (commutatif ou non) muni d'une valeur absolue. C'est un corps topologique pour la topologie définie par cette valeur absolue.
- Un module topologique sur un anneau topologique A est un module sur A muni d'une topologie pour laquelle il est un groupe topologique et pour laquelle la loi externe est continue.
- Un espace vectoriel topologique sur un corps topologique (par exemple le corps des nombres réels ou le corps des nombres complexes) est un module topologique sur ce corps topologique.
- Une algèbre topologique sur un anneau topologique commutatif A est une algèbre sur cet anneau topologique A, munie d'une topologie pour laquelle elle est un module topologique sur A et pour laquelle la multiplication est continue.
- Autre exemple, la structure algébrique peut être munie d'un écart, devenant un espace pseudométrique :
- Les espaces semi-normés (ou espaces vectoriels semi-normés) sont des espaces vectoriels réels ou complexes (ou sur un corps valué non discret) munis d'une semi-norme. Les espaces semi-normés sont des espaces pseudométriques, car il est toujours possible de construire un écart à partir d’une semi-norme : on prend comme écart entre deux vecteurs la semi-norme de leur différence.
- Plus particulièrement, la structure algébrique peut être munie d'une distance, devenant un espace métrique :
- Un cas important est celui des espaces vectoriels possédant une norme, qui définit la « longueur » d’un vecteur :
- Les espaces normés (ou espaces vectoriels normés) sont des espaces vectoriels réels ou complexes (ou sur un corps valué non discret) munis d'une norme. Les espaces normés sont des espaces métriques car il est toujours possible de construire une distance à partir d’une norme : on prend comme distance entre deux vecteurs la norme de leur différence.
- Un espace de Banach est un espace vectoriel normé complet.
- Un espace affine normé est un espace affine attaché à un espace vectoriel normé. C'est un espace métrique : il est possible de définir la distance entre deux points comme la norme du vecteur qui va du premier point au second.
- Les espaces préhilbertiens sont des espaces vectoriels réels ou complexes munis d'un produit scalaire. Ces espaces vectoriels sont des espaces normés : la norme d'un vecteur y est la racine carrée de son carré scalaire. Quelques cas importants ont reçu un nom :
- Un espace vectoriel euclidien est un espace vectoriel préhilbertien réel de dimension finie, muni d’un produit scalaire dont la forme quadratique correspondante est définie positive. Un espace affine euclidien est un espace affine attaché à un espace vectoriel euclidien, muni de la distance, dite euclidienne, déduite de la norme euclidienne. Cet espace est celui de la géométrie classique d’ Euclide.
- Un espace vectoriel hermitien est un espace vectoriel préhilbertien complexe de dimension finie.
- Un espace de Hilbert (ou espace hilbertien) est un espace préhilbertien complet. C’est donc un espace de Banach particulier. Les espaces vectoriels euclidiens et hermitiens sont des exemples d'espaces de Hilbert.
- Un cas important est celui des espaces vectoriels possédant une norme, qui définit la « longueur » d’un vecteur :
Structures et géométrie différentielle et algébrique
- Un groupe de Lie réel ou complexe est un groupe muni d'une structure de variété analytique réelle ou complexe (ou de variété différentielle dans le réel, c'est suffisant) pour laquelle la loi de composition est analytique (ou indéfiniment différentiable dans le cas réel), ainsi que l'application qui à un élément associe son inverse. Les groupes de Lie réels et complexes sont des groupes topologiques. Un groupe topologique est le groupe topologique sous-jacent à au plus un groupe de Lie réel, et ainsi on peut dire, sans ambiguïté, que certains groupes topologiques sont des groupes de Lie réels. On peut aussi définir les groupes de Lie sur un corps valué complet commutatif K dont la valeur absolue est non triviale (en particulier sur le corps des nombres p-adiques) en remplaçant les variétés analytiques réelles ou complexes par les variétés K-analytiques.
- Un espace homogène de Lie d'un groupe de Lie réel G est une variété différentielle X, munie d'un loi externe de G sur X qui est indéfiniment différentiable.
- Un groupe algébrique sur un corps commutatif algébriquement clos K est un groupe muni d'une structure de variété algébrique sur K pour laquelle la loi de composition est régulière, ainsi que l'application qui à un élément associe son inverse.
Structures algébriques et catégories
Toute structure algébrique possède sa propre notion d’homomorphisme, une application compatible avec ses lois de composition. En ce sens, toute structure algébrique définit une catégorie.
Notes et références
- Raymond Raffin, Anneaux non-associatifs, exposé au séminaire Dubreil (1950-1951) disponible en ligne.
- cette dernière propriété disparait dans la définition de l’anneau car elle est automatiquement vérifiée.
Bibliographie
- Serge Lang, Structures algébriques, Paris, InterEditions, coll. « Les cours de Serge Lang »,
- Jean-Luc Verley, « Algèbre », dans Dictionnaire de mathématiques – algèbre, analyse, géométrie, Paris, Encyclopædia Universalis et Albin Michel,


