Pseudo-anneau
En mathématiques, un pseudo-anneau est une des structures algébriques utilisées en algèbre générale. C'est un ensemble muni d'une addition et d'une multiplication qui vérifient les mêmes axiomes que celles d'un anneau, à ceci près qu'on n'exige pas la présence d'un élément neutre pour la multiplication[1].
Une minorité d'auteurs ne demandent pas aux anneaux d'avoir un neutre multiplicatif[2] ; si l'on se réfère à leurs conventions, le présent article traite donc de ce qu'ils appellent des anneaux.
Il est possible d'ajouter une unité à un anneau qui en est dépourvu, ceci de plusieurs façons. Dans une certaine mesure, ces techniques permettent d'utiliser la théorie des anneaux unitaires pour traiter de questions concernant les pseudo-anneaux.
Exemples
- Tous les anneaux (unitaires) sont a fortiori des pseudo-anneaux.
- L'ensemble 2Z des entiers relatifs pairs est un pseudo-anneau qui n'est pas un anneau.
- Un pseudo-anneau de carré nul[3] A est un pseudo-anneau dans lequel le produit de deux éléments vaut toujours 0. Un pseudo-anneau de carré nul qui est par ailleurs unitaire est forcément réduit à l'anneau nul. Tout groupe abélien (A, +) peut être muni d'une structure de pseudo-anneau de carré nul en posant xy = 0 pour tous x et y de A.
- L'ensemble des matrices à coefficients dans Z de la forme est un pseudo-anneau. Il a une infinité de neutres à gauche (toutes les matrices de la forme ) mais aucun d'entre eux n'est neutre à droite : ce n'est donc pas un anneau unitaire[4].
- De nombreuses algèbres associatives sur R ou C, qui jouent un rôle essentiel en analyse fonctionnelle, sont dépourvues d'élément neutre multiplicatif et sont à ce titre des pseudo-anneaux : ainsi l'espace noté des fonctions qui tendent vers zéro à l'infini sur R, ou l'espace de Schwartz des fonctions à décroissance rapide (muni de la multiplication usuelle des fonctions), l'espace L1 des fonctions Lebesgue-intégrables sur R (muni de la convolution) ou l'espace des opérateurs compacts d'un espace de Hilbert de dimension infinie (muni de la composition des opérateurs).
Un lemme
Si un pseudo-anneau a exactement un neutre à gauche, celui-ci est également neutre à droite, et le pseudo-anneau est donc un anneau unitaire[4].
Concepts de base
- Morphismes : on peut les définir[5] comme sur les anneaux, à ceci près qu'il n'y a que deux conditions à poser : un morphisme de pseudo-anneaux est une application entre deux pseudo-anneaux A et B qui vérifie, pour tous a et b :
- f(a + b) = f(a) + f(b)
- f(ab) = f(a)f(b).
- Sous-pseudo-anneaux : une sous-structure se définit ici comme un sous-groupe additif par ailleurs stable par multiplication[6].
- Idéaux et quotients : sans qu'il n'y ait rien à changer, on définit comme sur les anneaux les notions d'idéal à droite, d'idéal à gauche, d'idéal bilatère et de quotient par un idéal bilatère, ce quotient étant un pseudo-anneau[7].
- Éléments à dénomination spécifique : on définit exactement comme dans un anneau les puissances d'un élément x (à ceci près qu'il n'est plus possible de définir x0), les diviseurs de zéro, les éléments nilpotents, les éléments idempotents[8].
- Caractéristique : faute de neutre multiplicatif, on peut tout de même en donner une définition qui ne repose que sur la structure de groupe abélien comme suit : soit A un pseudo-anneau. S'il existe un entier n > 0 tel que nA = {0}, on appelle caractéristique de A le plus petit tel entier ; s'il n'en existe pas, on dit que A est de caractéristique nulle[9]. Lorsque l'anneau est unitaire, cette définition coïncide avec celle le plus habituellement fournie pour la caractéristique de celui-ci.
- Modules : on peut recopier la définition d'un module sur un anneau unitaire en y supprimant la condition relative au neutre multiplicatif (1x = x). Bourbaki appelle pseudomodule la structure ainsi définie[10].
Adjonction d'une unité
L'extension de Dorroh
Soit A un pseudo-anneau. Sur la somme directe externe Z ⊕ A des groupes abéliens additifs Z et A, on définit une multiplication en posant :
- (m + α)(n + β) = mn + nα + mβ + αβ pour tous m, n dans Z et tous α, β dans A.
On vérifie que cette multiplication est associative, et distributive par rapport à l'addition. De plus, 1 en est un élément neutre : on a donc construit un anneau unitaire.
Enfin, l'inclusion i de A dans Z ⊕ A est un morphisme de pseudo-anneaux : on a donc construit un anneau unitaire qui contient A. On l'appelle l'extension de Dorroh[11] de A. On le notera A1 dans la suite.
Il ressort immédiatement de la définition de A1 que A en est un idéal (bilatère).
Exemples :
- si A = XZ[X], l'idéal des multiples de X dans l'anneau des polynômes sur Z (c'est-à-dire les polynômes sans terme constant), l'extension de Dorroh renvoie Z[X] ;
- en revanche, si A = 2Z, l'idéal des entiers relatif pairs, l'extension de Dorroh ne retourne pas Z mais un anneau ayant pour groupe additif sous-jacent Z2 et qui contient des diviseurs de zéro ;
- si le pseudo-anneau A possédait déjà un neutre multiplicatif, qu'on notera ε, considérons F : Z × A → A1 définie par F(k,α) = k – kε + α. On vérifie que c'est un isomorphisme d'anneaux (où Z × A a été muni des opérations d'anneau produit). Dans ce cas, l'extension de Dorroh contient donc forcément des diviseurs de zéro et n'a guère d'intérêt, sinon comme exemple[12].
Sans être un procédé d'une efficacité absolue, l'extension de Dorroh permet néanmoins souvent de ramener l'étude d'un pseudo-anneau à celle d'un anneau unitaire[13]. En particulier, étant donné un pseudomodule sur A, on peut étendre son anneau de scalaires à A1 (par la formule (m + α)x = mx + αx) ; par ailleurs, tout module sur A1 devient un pseudomodule sur A par restriction des scalaires, ces deux transformations étant réciproques l'une de l'autre. Enfin, si l'on dispose de deux pseudomodules sur A, les morphismes entre eux sont les mêmes, que l'on considère leurs structures de pseudomodules ou leurs structures de modules sur A1. Les catégories des A-pseudomodules et des A1-modules sont donc exactement les mêmes[14].
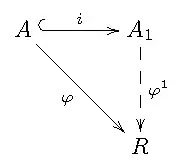
Enfin, l'extension de Dorroh vérifie la propriété universelle suivante[13] :
Soit A un pseudo-anneau, A1 son extension de Dorroh et i l'inclusion de A dans A1. Pour tout anneau unitaire R et tout morphisme de pseudo-anneaux φ : A → R, il existe un et un seul morphisme d'anneaux unitaires φ1 : A1 → R pour lequel φ = φ1 ∘ i.
L'extension de Szendrei
Soit maintenant A un pseudo-anneau sans diviseur de zéro. Dans l'extension de Dorroh A1, on note J l'ensemble des éléments c tels que cA = {0}, et l'on constate que J est un idéal bilatère de A1. On peut donc considérer l'anneau unitaire quotient A1/J.
Par ailleurs, en utilisant l'absence de diviseur de zéro dans A, on remarque que J ∩ A = {0} et A s'injecte donc encore dans A1/J : on a donc construit un nouvel anneau unitaire qui contient A (qui n'a rien de nouveau si J = {0}). On l'appelle l'extension de Szendrei.
Cette extension est elle-même un anneau sans diviseur de zéro.
Exemples :
- si A = XZ[X], l'idéal J est nul dans A1=Z[X] : l'extension de Szendrei coïncide avec l'extension de Dorroh ;
- si A est un anneau unitaire sans diviseur de zéro, de neutre noté ε, on constate que J est l'ensemble des m(1 – ε), m parcourant Z, puis que l'extension de Szendrei de A est égale à A ;
- pour A = 2Z, notons η l'élément 2 de A (c'est nécessaire pour éviter les collisions de notations dans Z ⊕ A = Z1 ⊕ Zη). On vérifie alors que J = Z(2-η), puis que l'extension de Szendrei de A n'est autre que l'inclusion de 2Z dans Z.
L'extension de Szendrei vérifie la propriété de minimalité suivante (théorème de Szendrei)[15] :
Soit A un pseudo-anneau sans diviseur de zéro et S son extension de Szendrei. Alors S est un anneau unitaire sans diviseur de zéro ; de plus, toute extension unitaire sans diviseur de zéro de A contient S comme sous-anneau.
La deuxième partie de l'énoncé doit être comprise au sens formel suivant : si l'on note i l'inclusion de A dans S, pour tout morphisme de pseudo-anneaux injectif φ : A → T vers un anneau unitaire sans diviseur de zéro noté T, il existe un morphisme d'anneaux unitaires injectif ψ : S → T pour lequel φ = ψ ∘ i.
Idéaux maximaux dans les pseudo-anneaux
Dans cette section, tous les anneaux sont supposés commutatifs.
On peut définir dans un pseudo-anneau commutatif un idéal premier en reprenant une des formes alternatives de la définition d'un idéal premier dans un anneau unitaire :
Un idéal I d'un pseudo-anneau A est dit premier lorsqu'il est différent de A et, pour tous x, y de A,
- xy ∈ I ⇒ x ∈ I ou y ∈ I.
Par le même raisonnement qu'en présence d'un neutre, on obtient la même conclusion, qui demande juste reformulation :
Un idéal I d'un pseudo-anneau commutatif A est premier si et seulement si l'anneau quotient de A par I n'est pas réduit à {0} et ne possède pas de diviseurs de zéro.
De même, on peut définir un idéal maximal d'un pseudo-anneau commutatif A comme un idéal qui est maximal dans l'ensemble (ordonné par l'inclusion) des idéaux de A autres que A lui-même.
En voici un exemple. Dans le pseudo-anneau commutatif 2Z, le sous-groupe additif 4Z est manifestement un idéal maximal. Pourtant l'anneau quotient de A par I n'est pas un corps commutatif, mais est le pseudo-anneau de carré nul à deux éléments. En outre, 4Z n'est pas premier, quoique maximal. On peut déjà retenir de cet exemple que :
Dans les pseudo-anneaux commutatifs, il existe des idéaux maximaux non premiers[16].
Pour mémoire, on rappelle qu'en théorie des anneaux commutatifs unitaires, les idéaux maximaux sont caractérisés par la production d'un anneau quotient qui est un corps. Un énoncé analogue quoique plus lourd existe.
Un idéal I d'un pseudo-anneau commutatif A est maximal si et seulement si l'anneau quotient de A par I est soit un corps, soit un pseudo-anneau de carré nul sur un groupe additif cyclique de cardinal premier[17].
Une autre différence avec la théorie des anneaux unitaires concerne le théorème de Krull. Les démonstrations de celui-ci reposent de façon cruciale sur la présence d'une unité dans l'anneau ; en effet, on y utilise la stabilité de la classe des idéaux propres (c.-à-d. strictement inclus dans l'anneau) par union croissante, stabilité qui se justifie par le fait qu'une union croissante d'idéaux propres, qui est clairement un idéal, ne contient pas 1 donc est encore propre. Non seulement cet argument de démonstration tombe si l'on considère des pseudo-anneaux, mais aussi le théorème, comme le montre l'exemple suivant.
Soit k un corps commutatif. On note A l'anneau :
(on entend par cette notation le quotient ).
Dans cet anneau commutatif unitaire A, on considère l'idéal P engendré par les puissances fractionnaires de X, c'est-à-dire :
qui est manifestement un idéal maximal. On introduit alors l'anneau local AP localisé de A en P, et l'on note T l'unique idéal maximal de AP. Dit plus concrètement, T est donc l'ensemble des éléments du corps des fractions de A qui ont une expression de la forme :
dans laquelle c, a1,...,am,b1,...,bn sont des scalaires tandis que les exposants r, s1,...,sm,t1,...,tn sont des nombres rationnels strictement positifs.
Le pseudo-anneau commutatif T défini ci-dessus n'a aucun idéal maximal[18].
Notes et références
- N. Bourbaki, Algèbre, Hermann, , I.93.
- Ainsi :
- (en) Neal H. McCoy, The Theory of Rings, MacMillan, (ISBN 978-1-124-04555-9),
- (en) David M. Burton, A First Course in Rings and Ideals, Addison-Wesley, ,
- (en) Joseph Gallian, Contemporary Abstract Algebra, Houghton Mifflin, (ISBN 978-0-618-51471-7) ou
- Jacqueline Lelong-Ferrand et Jean-Marie Arnaudiès, Cours de mathématiques, t. 1 : Algèbre, Dunod, , p. 79.
- Bourbaki 1970, p. I-97.
- McCoy 1964, p. 9, exercices 15 et 16.
- McCoy 1964, p. 43.
- McCoy 1964, p. 2.
- McCoy 1964, p. 21-22.
- McCoy 1964, p. 3-5.
- McCoy 1964, p. 4 ou Burton 1970, p. 11. On trouve une définition différente à la marge dans László Rédei, Algebra, Pergamon Press, , vol. 1, p. 64 : parmi les Z-modules à annulateur trivial, il distingue ceux où tout élément (non nul) est d'ordre (additif) infini et les déclare de caractéristique nulle, mais il définit les autres comme étant « de caractéristique infinie ».
- (en) Pierre-Antoine Grillet, Abstract Algebra, New York, Springer-Verlag, , 669 p. (ISBN 978-0-387-71567-4), p. 315 sous le nom de « module » ou Bourbaki 1970, p. II-177 sous le nom de « pseudomodule ».
- Rédei 1967, p. 110, qui attribue l'invention de cette extension à (en) I. L. Dorroh, « Concerning adjunctions to algebra », Bull. Amer. Math. Soc., vol. 38, , p. 85-88.
- Burton 1970, p. 31-32, écrit qu'elle n'a « pas de mérite particulier ». La structure comme anneau-produit est signalée dans Bourbaki 1970, p. II.177.
- Grillet 2007, p. 108.
- Bourbaki 1970, p. II-177.
- Rédei 1967, p. 335-337 (pour l'ensemble de la section relative à l'extension de Szendrei), qui renvoie à l'article : (en) J. Szendrei, « On the extension of rings without divisors de zero », Acta Sci. Math. Szeged, vol. 13, 1949-1950, p. 231-234.
- Burton 1970, p. 75-77.
- Rédei 1967, p. 205-206, fournit un énoncé un peu plus technique ne supposant pas la commutativité. L'énoncé donné ici est conséquence immédiate des informations p. 133 dans (en) Oscar Zariski et Pierre Samuel, Commutative Algebra, t. 1, Van Nostrand, .
- Les remarques sur la preuve du théorème de Krull figurent dans Burton 1970, p. 75-77. L'exemple fourni est l'exemple 149 p. 129 dans (en) Harry C. Hutchins, Examples of Commutative Rings, Polygonal Pub House, , 167 p. (ISBN 978-0-936428-05-5), qui n'en signale pas cette propriété mais c'est un exercice sans difficulté.



![A:=k[X,X^{{1/2}},X^{{1/3}},X^{{1/4}},\ldots ].](https://img.franco.wiki/i/c17a26dc7793f3de989fd49abd7781caefe9287f.svg)
![k[Y_{1},Y_{2},Y_{3},\ldots ]/(Y_{1}-Y_{2}^{2},Y_{1}-Y_{3}^{3},\ldots )](https://img.franco.wiki/i/ab65cffd00284354beb39d65458657a240eb464b.svg)

