Groupe des quaternions
En mathématiques et plus précisément en théorie des groupes, le groupe des quaternions est l'un des deux groupes non abéliens d'ordre 8.
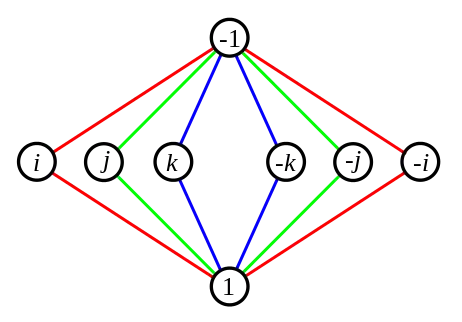
Il admet une représentation réelle irréductible de degré 4, et la sous-algèbre des matrices 4×4 engendrée par son image est un corps gauche qui s'identifie au corps des quaternions de Hamilton.
Définition
Le groupe des quaternions est souvent désigné par le symbole Q ou Q8 et est écrit sous forme multiplicative, avec les 8 éléments suivants :
Ici, 1 est l'élément neutre, et pour tout a dans Q. Les règles de multiplication restantes peuvent être obtenues à partir de l'associativité et de la relation suivante :
Table du groupe
La table de multiplication pour Q est donnée par :
| 1 | i | j | k | -1 | -i | -j | -k | |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | i | j | k | -1 | -i | -j | -k |
| i | i | -1 | k | -j | -i | 1 | -k | j |
| j | j | -k | -1 | i | -j | k | 1 | -i |
| k | k | j | -i | -1 | -k | -j | i | 1 |
| -1 | -1 | -i | -j | -k | 1 | i | j | k |
| -i | -i | 1 | -k | j | i | -1 | k | -j |
| -j | -j | k | 1 | -i | j | -k | -1 | i |
| -k | -k | -j | i | 1 | k | j | -i | -1 |
Le groupe ainsi obtenu est non abélien, comme on peut le voir sur la relation . Cependant Q est un groupe hamiltonien : tout sous-groupe de Q est normal, mais Q est non abélien. Tout groupe hamiltonien contient une copie de Q.
Propriétés
Représentation
Considérant un espace vectoriel réel de dimension 4 dont une base est notée {1, i, j, k}, on le munit d'une structure d'algèbre associative en utilisant la table de multiplication ci-dessus et la distributivité. Le résultat est un corps gauche appelé le corps des quaternions. Le lemme de Schur généralise cette approche. Il montre en effet que l'algèbre (associative) des endomorphismes de toute représentation irréductible d'un groupe est une algèbre à division donc un corps, parfois non commutatif.
Inversement, on peut démarrer avec le corps des quaternions et définir le groupe des quaternions comme le sous-groupe multiplicatif constitué des 8 éléments .
Sur tout corps de caractéristique différente de 2, le théorème de Maschke réduit l'étude des représentations de Q à celle de ses représentations irréductibles.
Représentations rationnelles et réelles
Faisons l'inventaire plus précis des représentations irréductibles de Q, à coefficients rationnels (ou réels, par extension des scalaires), et la description de celle de degré 4 à laquelle il est fait implicitement allusion ci-dessus.
- On construit la représentation régulière λ (à coefficients rationnels) du groupe Q et de son algèbre ℚ[Q] en les faisant agir sur ℚ[Q] par multiplication à gauche. Comme toute représentation régulière d'algèbre unifère, λ est fidèle (car λ(x)(1) = x). Notons (δg)g∈Q la base canonique de l'espace vectoriel ℚ[Q] ≃ ℚQ ≃ ℚ8.
- La somme v1 des 8 vecteurs de cette base est fixe par tous les λ(g) donc la sous-représentation λ1, sur la droite vectorielle V1 := ℚv1, est la représentation unité de Q.
- Il existe trois autres droites stables et sous-représentations de degré 1, notées Vq = ℚvq et λq pour q = i, j, k : par exemple, vi := (δ1 + δ–1 + δi + δ–i) – (δj + δ–j + δk + δ–k) est envoyé sur lui-même par λ(±1) et λ(±i), et sur son opposé par λ(±j) et λ(±k).
- Enfin, les quatre vecteurs wq := δq – δ–q pour q = 1, i, j, k engendrent un sous-espace W de dimension 4 supplémentaire de la somme (directe) des quatre droites précédentes. On vérifie que W est stable par λ : pour tout g ∈ Q, λ(g)(wq) = εwq', où ε ∈ {+, –} et q' ∈ {1, i, j, k} sont déterminés par l'égalité (dans Q) gq = εq'. Dans la sous-représentation correspondante de l'algèbre (en) ℚ[Q], que nous noterons w, on remarque que w(δ–q) = –w(δq), c'est-à-dire que w se factorise par une représentation w' de l'algèbre quotient Hℚ des « quaternions à coefficients rationnels » (pour une description matricielle de w', voir la représentation des quaternions comme matrices 4×4 de réels). Cette représentation w' est simplement la représentation régulière de l'algèbre Hℚ (dont l'espace vectoriel s'identifie naturellement à W). L'irréductibilité de w' (donc celle de w) vient du fait que tout élément non nul x de Hℚ est inversible donc Hℚx = Hℚ.
La représentation régulière de Q est donc somme directe de cinq représentations irréductibles : quatre de degré 1 (non équivalentes) et une de degré 4. Le morphisme d'algèbres est injectif donc (par comparaison des dimensions) c'est un isomorphisme.
Représentations complexes
Sur ℂ, le groupe Q a également cinq représentations irréductibles, calculées dans l'article détaillé : les quatre caractères réels λ1, λi, λj, λk ci-dessus et une représentation ρ, de degré 2 donc non réelle (en) (c'est un exemple de représentation induite, que l'on peut expliciter matriciellement). L'algèbre ℂ[Q] est donc isomorphe à ℂ4⊕M2(ℂ).
On peut remarquer que la représentation réelle w ci-dessus est équivalente à celle obtenue à partir de ρ en considérant ℂ2 comme un espace réel de dimension 4, et que w⊗ℂ est équivalente à ρ ⊕ ρ.
Nature du groupe
Les trois éléments i, j et k sont tous d'ordre 4 dans Q et deux quelconques d'entre eux engendrent le groupe entier. Q admet la présentation
On peut prendre, par exemple, x = i et y = j.
Tous les sous-groupes propres de Q sont cycliques.
Le centre et le sous-groupe des commutateurs de Q est le sous-groupe {±1}. Le groupe quotient Q/{±1} est isomorphe au groupe de Klein V. Il y a cinq classes de conjugaison : {1}, {-1}, {i, -i}, {j, -j} et {k, -k}.
Le groupe des automorphismes intérieurs de Q est isomorphe à Q modulo son centre, et est par conséquent aussi isomorphe au groupe de Klein. Le groupe des automorphismes de Q est isomorphe au groupe symétrique S4. Le groupe des automorphismes extérieurs de Q est alors S4/V qui est isomorphe à S3.
Le groupe des quaternions Q peut aussi être vu comme un sous-groupe normal d'indice 3 du groupe spécial linéaire SL(2, F3)[1].
Groupe de quaternions généralisé
Les groupes de quaternions généralisés sont les 2-groupes dicycliques, c'est-à-dire que (pour n ≥ 3), le groupe de quaternions généralisé d'ordre 2n est le groupe de présentation
Le groupe de quaternions ordinaire correspond au cas n = 3. Le groupe peut être réalisé comme le sous-groupe des quaternions unitaires engendré par et .
Le quotient de par son centre est isomorphe au groupe diédral [2] donc est nilpotent de classe n – 1.
Les groupes de quaternions généralisés ont la propriété que chaque sous-groupe abélien est cyclique. On peut prouver[3] qu'un p-groupe fini possédant cette propriété (chaque sous-groupe abélien est cyclique) est soit un groupe cyclique, soit un groupe de quaternions généralisé.
Notes et références
- Pour une image, voir Visualisation de GL(2,p).
- (en) Joseph J. Rotman (en), An Introduction to the Theory of Groups [détail des éditions], 1995, 4e éd., exerc. 4.42, p. 88.
- Pour une démonstration, voir par exemple (en) I. Martin Isaacs (en), Finite Group Theory, AMS, (lire en ligne), p. 278-284, théorème 6.12, p. 189 (dont le présent énoncé se déduit immédiatement), ou encore (en) Hans Kurzweil (de) et Bernd Stellmacher, The Theory of Finite Groups, An Introduction, Springer, (lire en ligne), énoncé 5.3.8, p. 115.
Voir aussi
Articles connexes
- Quaternions de Hurwitz
- Liste des petits groupes
- Groupe de Heisenberg sur F2 ≃ Groupe diédral D8 (le seul autre groupe non abélien d'ordre 8, à isomorphisme près)
Liens externes
- (en) Vipul Naik, « Quaternion group », sur groupprops
- Bruno Vallette, « Le groupe ℍ8 », (énoncé et corrigé d'un examen de L3 à l'université Nice-Sophia-Antipolis)






![{\displaystyle \mathbb {Q} [Q]\to \mathbb {Q} ^{4}\oplus {\rm {H}}_{\mathbb {Q} },x\mapsto (\lambda _{1}(x),\lambda _{\rm {i}}(x),\lambda _{\rm {j}}(x),\lambda _{\rm {k}}(x),w(x)(1))}](https://img.franco.wiki/i/fa17836e76455eaf8bfc0ec834df504a36970570.svg)





