Règle de Littlewood-Richardson

En mathématiques, et notamment en combinatoire algébrique la règle de Littlewood-Richardson est une description combinatoire des coefficients qui apparaissent dans la décomposition du produit de deux polynômes de Schur en combinaison linéaire d'autres polynômes de Schur. Ces coefficients sont des entiers naturels. La règle de Littlewood-Richardson les interprète comme le nombre de tableaux de Young particuliers. Ces coefficients se rencontrent dans de nombreux autres contextes mathématiques, Par exemple, il dénotent la multiplicité dans la décomposition des produits tensoriel de représentations irréductibles du groupe général linéaire (ou de groupes voisins comme le groupe spécial linéaire et le groupe spécial unitaire), ou également dans la décomposition de certaines représentations induite dans les représentations du groupe symétrique.

Un coefficient de Littlewood-Richardson dépend de trois partitions $\lambda ,\mu ,\nu$ , où $\lambda$ et $\mu$ paramètrent les fonctions de Schur à multiplier, et où $\nu$ est l'indice de la fonction de Schur dont il est le coefficient dans la combinaison linéaire ; ce sont les coefficients $c_{\lambda ,\mu }^{\nu }$ tels que $s_{\lambda }s_{\mu }=\sum _{\nu }c_{\lambda ,\mu }^{\nu }s_{\nu }.$ La règle de Littlewood-Richardson donne l'interprétation combinatoire suivante de ces coefficients (les tableaux de Littlewood-Richardson sont définis plus bas) :

Règle de Littlewood-Richardson — Le coefficient $c_{\lambda ,\mu }^{\nu }$ de la décomposition

s_{\lambda }s_{\mu }=\sum _{\nu }c_{\lambda ,\mu }^{\nu }s_{\nu }

est égal au nombre de tableaux de Littlewood-Richardson de forme $\nu /\lambda$ et de poids $\mu$ .

Tableaux de Littlewood-Richardson

Définitions

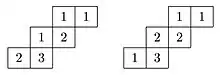
Fig. 1.- Les deux tableaux de Littlewood-Richardson de forme (4,3,2)/(2,1) et de poids (3,2,1).

Étant donné un tableau de Young semi-standard gauche $T$ , le mot de $T$ est la suite $w(T)$ obtenue en concaténant les lignes de $T$ , lues de droite à gauche. Par exemple, le mot du premier des tableaux de la figure 1 ci-contre est $112132$ .

Un tableau de Littlewood-Richardson est un tableau semi-standard gauche vérifiant la propriété supplémentaire que son mot de tableau est un mot de Yamanouchi gauche (ou mot de treillis), c'est-à-dire tel que dans tout préfixe, le nombre $i$ apparaît au moins aussi souvent que le nombre $i+1$ . Le mot $112132$ est bien un mot de Yamanouchi.

Une autre caractérisation (dont l’équivalence n’est pas immédiate) est que le poids du tableau et de chaque tableau obtenu en supprimant des colonnes à gauche, est décroissant au sens large. Par exemple, les poids du tableau de gauche de la figure 1 et de ses tableaux successifs sont (3,2,1), (3,1,1), (2,1), (1). D'autres notions combinatoires sont en bijection avec les tableaux de Littlewood-Richardson et peuvent donc servir à les définir.

Le coefficient de Littewood-Richardson $c_{\lambda ,\mu }^{\nu }$ est le nombre de tableaux de Littlewood-Richardson de forme $\nu /\lambda$ et de poids $\mu$ .

Fig. 2.- Seul le deuxième de ces deux tableaux est un tableau de Littlewood-Richardson. Son mot de Yamanouchi est 1112132243.

Exemple

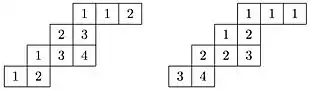
On considère les tableaux gauches de la figure 1. Ce sont des tableaux gauches de forme $\nu /\lambda$ et de poids $\mu$ , avec $\lambda =(2,1)$ , $\mu =(3,2,1)$ and $\nu =(4,3,2)$ . Le deuxième des tableaux a pour mot 112213, c'est donc aussi un tableau de Littlewood-Richardson.

Pour vérifier que $c_{\lambda ,\mu }^{\nu }=2$ , on va montrer que les deux tableaux donnés à droite sont les seuls tableaux de forme $\nu /\lambda$ et poids $\mu$ qui sont des tableaux de Littlewood-Richardson. En effet, la dernière cellule de la première ligne doit contenir le nombre 1. Mais alors la première ligne ne contient que des 1 (ceci est le cas pour tout tableau de Littlewood-Richardson, et montre donc tout de suite que le premier des tableaux de la figure 2 n'est pas un mot de Littlewood-Richardson). La dernière cellule de la deuxième ligne contient un 2 car les colonnes sont strictement croissantes et que l'on ne peut placer un entier plus grand avant d'avoir placé un 2 par la condition de Yamanouchi. La première cellule de la deuxième ligne contient soit 1 soit 2. Ceci détermine les entrées de la troisième ligne qui sont croissantes au sens large et doivent assurer que le poids est (3,2,1). Ceci donne deux possibilités qui s'avèrent être tous deux des tableaux de Littlewood-Richardson.

Une description plus géométrique

On peut remplacer la condition que les entrées d'un tableau, lus dans l'ordre, forment un mot de Yamanouchi, par une condition locale, plus géométrique. On numérote les occurrences d'un nombre dans le tableau dans l'ordre dans lesquelles elles apparaissent dans le mot du tableau formé des lignes, candidat à être un mot de Yamanouchi. Appelons index l'ordre d'apparition, et notons $i[j]$ pour l’occurrence de $i$ d'index $j$ . Le mot du premier tableau de la figure 1, à savoir $w=112132$ , devient le mot « décoré » $1[1]1[2]2[1]1[3]3[1]2[2]$ .

Maintenant, si un tableau de Littlewood-Richardson contient une entrée $i>1$ d'index $j$ , cette entrée apparaît après l'occurrence de $i-1$ d'index $j$ dans le mot du tableau par la condition de Yamanouchi, et en fait dans une ligne strictement en-dessous de la ligne de $i-1$ parce que les lignes sont croissantes. En fait, l'occurrence $i[j]$ doit aussi figurer dans une colonne qui n’est pas plus à droite que l'entrée $i-1[j]$ (ce qui semble à première vue une condition plus restrictive).

Si le poids du tableau de Littlewood-Richardson est donné, on peut former une collection d'entrées indexées, puis les placer de manière à respecter ces restrictions géométriques, en plus de celles de la définition des tableaux semi-standard et enfin la condition que l'ordre des occurrences d'un même nombre respecte l'ordre de ses index, alors on est assuré que les tableaux obtenus sont des tableaux de Littlewood-Richardson.

Esquisse d'une forme algorithmique de la règle

La règle de Littlewood-Richardson énoncée plus haut donne une expression combinatoire pour les coefficients de Littlewood-Richardson, mais ne donne pas d'indication immédiate sur une méthode pratique pour énumérer les tableaux de Littlewood-Richardson en vue de trouver les valeurs de ces coefficients.

Pour déterminer les coefficients $c_{\lambda ,\mu }^{\nu }$ pour $\lambda$ et $\mu$ fixés, il faut faire varier le tableau « extérieur » correspondant à $\nu$ . Mais comme le poids $\mu$ est donné, l'ensemble des entrées indexées de la description géométrique est fixé. Une exploration systématique repose sur un examen des entrées par ordre croissant, alors que pour des entrées égales, on peut opérer par index décroissant : l'entrée $i[j]$ doit être dans une colonne à droite de $i[j+1]$ , mais pas plus loin que $i-1[j]$ (si cette entrée existe). Ceci restreint de manière efficace le nombre de positions candidates mais conserve toujours une position possible pour $i[j]$ .

Exemples

Les coefficients de Littlewood-Richardson sont les coefficients de l'écriture d'un produit de polynômes de Schur dans la base de ces polynômes, au moyen de la formule

s_{\lambda }s_{\mu }=\sum c_{\lambda \mu }^{\nu }s_{\nu }.

La liste ci-dessous contient tous les coefficients $c_{\lambda \mu }^{\nu }$ pour $|\nu |\leq 4$ . De plus, on a $s_{0}s_{\pi }=s_{\pi }$ pour tout $\pi$ , où $s_{0}=1$ est le polynôme de Schur de la partition vide.

{\begin{array}{l}s_{1}s_{1}=s_{2}+s_{11}\\s_{2}s_{1}=s_{3}+s_{21}\\s_{11}s_{1}=s_{111}+s_{21}\\s_{3}s_{1}=s_{4}+s_{31}\\s_{21}s_{1}=s_{31}+s_{22}+s_{211}\\\end{array}}\qquad \qquad {\begin{array}{l}s_{2}s_{2}=s_{4}+s_{31}+s_{22}\\s_{2}s_{11}=s_{31}+s_{211}\\s_{111}s_{1}=s_{1111}+s_{211}\\s_{11}s_{11}=s_{1111}+s_{211}+s_{22}\end{array}}

Pour les petites partitions, les coefficients sont en général 0 ou 1, et cela se produit aussi quand un des facteurs est $s_{n}$ ou $s_{11\cdots 1}$ à cause de la formule de Pieri (en) ou sa transposée. Le cas le plus simple d'un coefficient plus grand que 1 est obtenu quand aucun des deux facteurs n'est de cette forme ; par exemple :

s_{21}s_{21}=s_{42}+s_{411}+s_{33}+2s_{321}+s_{3111}+s_{222}+s_{2211}.

L'expression devient vite plus compliquée pour des partitions plus grandes. Par exemple :

{\begin{array}{ll}s_{321}s_{321}&=s_{642}+s_{6411}+s_{633}+2s_{6321}+s_{63111}+s_{6222}+s_{62211}+s_{552}\\&+s_{5511}+2s_{543}+4s_{5421}+2s_{54111}+3s_{5331}+3s_{5322}+4s_{53211}+s_{531111}+2s_{52221}\\&+s_{522111}+s_{444}+3s_{4431}+2s_{4422}+3s_{44211}+s_{441111}+3s_{4332}+3s_{43311}+4s_{43221}\\&+2s_{432111}+s_{42222}+s_{422211}+s_{3333}+2s_{33321}+s_{333111}+s_{33222}+s_{332211}\end{array}}

avec un total de 34 termes et la somme des coefficients (multiplicité) égale à 62, le plus grand coefficient est 4.

Voici d'autres exemples :

$s_{4321}s_{4321}$ est la somme de 206 termes avec multiplicité totale 930, le plus grand coefficient est 18;
$s_{54321}s_{54321}$ est la somme de 1433 termes avec multiplicité totale 26704, le plus grand coefficient (celui de $s_{86543211}$ ) est 176;
$s_{654321}s_{654321}$ est la somme de 10873 termes avec multiplicité totale 1458444, le plus grand coefficient est 2064, la valeur moyenne ds coefficients est plus que 100.

L'exemple original de Littlewood et Richardson

L'exemple original de (Littlewood et Richardson 1934, p. 122-124) est le suivant (après une correction qui concerne 3 tableaux qu'ils avaient trouvés mais oublié d'inclure dans la somme finale) :

{\begin{array}{ll}s_{431}s_{221}&=s_{652}+s_{6511}+s_{643}\\&+2s_{6421}+s_{64111}+s_{6331}+s_{6322}+s_{63211}+s_{553}+2s_{5521}+s_{55111}+2s_{5431}\\&+2s_{5422}+3s_{54211}+s_{541111}+s_{5332}+s_{53311}+2s_{53221}+s_{532111}+s_{4432}\\&+s_{44311}+2s_{44221}+s_{442111}+s_{43321}+s_{43222}+s_{432211}\end{array}}

Ses 26 termes proviennent de 34 tableaux suivants:

....11 ....11 ....11 ....11 ....11 ....11 ....11 ....11 ....11    
...22  ...22  ...2   ...2   ...2   ...2   ...    ...    ...
.3     .      .23    .2     .3     .      .22    .2     .2     
       3             3      2      2      3      23     2      
                                   3                    3
....1  ....1  ....1  ....1  ....1  ....1  ....1  ....1  ....1   
...12  ...12  ...12  ...12  ...1   ...1   ...1   ...2   ...1
.23    .2     .3     .      .23    .22    .2     .1     .2      
       3      2      2      2      3      23     23     2
                     3                                  3      
....1  ....1  ....1  ....1  ....1  ....1  ....1  ....1   
...2   ...2   ...2   ...    ...    ...    ...    ...    
.1     .3     .      .12    .12    .1     .2     .2      
2      1      1      23     2      22     13     1
3      2      2             3      3      2      2
              3                                  3
....   ....   ....   ....   ....   ....   ....   ....   
...1   ...1   ...1   ...1   ...1   ...    ...    ...    
.12    .12    .1     .2     .2     .11    .1     .1      
23     2      22     13     1      22     12     12
       3      3      2      2      3      23     2
                            3                    3

Le calcul des fonctions de Schur gauches est similaire. Par exemple, les 15 tableaux de Littlewood-Richardson pour $\nu =(5,4,3,2)$ et $\lambda =(3,3,1)$ sont :

...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11 ...11
...2  ...2  ...2  ...2  ...2  ...2  ...2  ...2  ...2  ...2  ...2  ...2  ...2  ...2  ...2
.11   .11   .11   .12   .11   .12   .13   .13   .23   .13   .13   .12   .12   .23   .23
12    13    22    12    23    13    12    24    14    14    22    23    33    13    34

de sorte que

s_{5432/331}=\sum c_{\lambda \mu }^{\nu }s_{\mu }=s_{52}+s_{511}+s_{4111}+s_{2221}+2s_{43}+2s_{3211}+2s_{322}+2s_{331}+3s_{421}

(Fulton 1997, p. 64).

Généralisation et cas particuliers

Fonctions de Schur gauches

(Zelevinsky 1981) étend la règle de Littlewood-Richardson comme suit aux fonctions de Schur gauches : $s_{\lambda }s_{\mu /\nu }=\sum _{\lambda +\omega (T_{\geq j})\in P}s_{\lambda +\omega (T)}$ où la somme est sur tous les tableaux $T$ sur $\mu /\nu$ tels que la suite $\lambda +\omega (T_{\geq j})$ est décroissante au sens large, et où $\omega (X)$ est le poids de $X$ . Dans cette écriture, $T_{\geq j}$ dénote le tableau obtenu à partir de $T$ en ne conservant que les colonnes d'indices $j,j+1,\dots$ .

Formule de Pieri

La formule de Pieri (en) est le cas particulier de la règle de Littlewood-Richardson où le diagramme de Ferrers d'une des deux partitions n'a qu'une seule ligne (partition en une seule part). Elle s'énonce :

$\displaystyle s_{\mu }s_{n}=\sum _{\lambda }s_{\lambda }$

où $s_{n}$ est la fonction de Schur de la partition de $n$ en une seule part, et la somme est sur toutes les partitions $\lambda$ obtenues à partir de $\mu$ en ajoutant $n$ éléments à son diagramme de Ferrers, avec au plus un élément par colonne.

Partitions rectangulaires

Lorsque les deux partitions $\lambda$ et $\mu$ ont une forme « rectangulaire », c'est-à-dire lorsque toutes leurs parts sont égales, les coefficients $c_{\lambda \mu }^{\nu }$ dans la règle de Littlewood-Richardson valent 0 ou 1 (Okada 1998). De plus, on peut donner une construction géométrique des partitions $\nu$ . Plus précisément, soient $a,b,p,q$ des entiers positifs avec $p\geq q$ . Notons $(a^{p})$ une partition en $p$ parts toutes égales à $a$ , de sorte que son diagramme de Ferrers est un rectangle de largeur $a$ et de hauteur $p$ . Les partitions qui sont les indices de termes non nuls du produit $s_{(a^{p})}s_{(b^{q})}$ sont les partitions $\nu$ de longueur $\leq p+q$ qui vérifient les trois conditions :

$\nu _{i}+\nu _{p+q-i+1}=a+b,\quad {i=1,\dots ,q}$ ;
$\nu _{q}\geq \max(a,b)$ ;
$\nu _{q+1}=\nu _{q+2}=\cdots =\nu _{p}=a$ .

Exemple de produit de formes rectangulaires

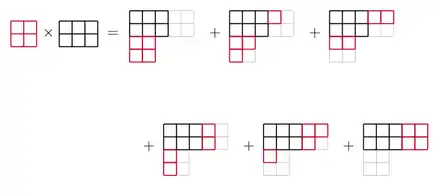
Voici un exemple. On prend $a=3,b=2,p=q=2$ . Le produit $s_{(3^{2})(2^{2})}$ fait intervenir 6 partitions; on a en effet

s_{(3^{2})(2^{2})}=s_{3322}+s_{4321}+s_{532}+s_{4411}+s_{541}+s_{55}

La figure les représente schématiquement. Le premier diagramme est la superposition des partitions $(3^{2})$ et $(2^{2})$ ; chacun des diagrammes suivants s'obtient en découpant une partie du rectangle inférieur et en la collant, après une rotation si nécessaire, à la droite du rectangle supérieur. Les conditions énoncées ci-dessus se réduisent, dans l'exemple, à :

\nu _{1}+\nu _{4}=5,\nu _{2}+\nu _{3}=5,\nu _{2}\geq 3

Utilisations des coefficients de Littlewood-Richardson

Les coefficients de Littlewood-Richardson $c_{\lambda \mu }^{\nu }$ apparaissent dans les contextes suivants :

Ce sont les constantes dans la décomposition d'un produit, dans l'anneau des fonctions symétriques, sur la base des fonctions de Schur : $s_{\lambda }s_{\mu }=\sum c_{\lambda \mu }^{\nu }s_{\nu }$ ou, de manière équivalente, $c_{\lambda \mu }^{\nu }$ est le produit scalaire de $s_{\nu }$ et du produit $s_{\lambda }s_{\mu }$ : $c_{\lambda \mu }^{\nu }=\langle s_{\nu },s_{\lambda }s_{\mu }\rangle$ .
Elles expriment les polynômes de Schur gauches en termes de fonctions de Schur par : $s_{\nu /\lambda }=\sum _{\mu }c_{\lambda \mu }^{\nu }s_{\mu }.$
Les coefficients apparaissent comme nombre d'intersection dans une grassmannienne : $\sigma _{\lambda }\sigma _{\mu }=\sum c_{\lambda \mu }^{\nu }\sigma _{\nu }$ , où $\sigma _{\mu }$ est la classe de la variété de Schubert (en) de la grassmannienne correspondant à $\mu$ .
$c_{\lambda \mu }^{\nu }$ est le nombre de fois que la représentation irréductible $V_{\lambda }\otimes V_{\mu }$ du produit des groupes symétriques $S_{|\lambda |}\times S_{|\mu |}$ apparait dans la restriction de la représentation $V_{\nu }$ de $S_{|\nu |}$ à $S_{|\lambda |}\times S_{|\mu |}$ . Par la formule de réciprocité de Frobenius, c'est aussi le nombre de fois que $V_{\nu }$ apparait dans la représentation de $S_{|\nu |}$ induite par $V_{\lambda }\otimes V_{\mu }$ .
Les nombres $c_{\lambda \mu }^{\nu }$ apparaissent dans la décomposition du produit tensoriel (Fulton 1997) de deux modules de Schur (en) (représentations irréductible de groupes spéciaux linéaires) : $E^{\lambda }\otimes E^{\mu }=\bigoplus _{\nu }(E^{\nu })^{\oplus c_{\lambda \mu }^{\nu }}.$
$c_{\lambda \mu }^{\nu }$ est le nombre de tableaux de Young standard de forme $\nu /\mu$ qui sont équivalents, au sens du jeu de taquin de Schützenberger à un tableau de Young standard fixe de forme $\lambda$ .
$c_{\lambda \mu }^{\nu }$ est aussi le nombre de bijections particulières appelées pictures en anglais (en) entre $\mu$ et $\nu /\lambda$ .

Historique

Unfortunately the Littlewood–Richardson rule is much harder to prove than was at first suspected. The author was once told that the Littlewood–Richardson rule helped to get men on the moon but was not proved until after they got there.
Gordon D. James (1987)[1]

La règle de Littlewood-Richardson a été énoncée par Dudley E. Littlewood et Archibald Read Richardson en 1934 (Littlewood et Richardson 1934, theorem III p. 119), mais n'a été démontrée dans cet article que dans des cas particuliers plutôt simples.

Gilbert de Beauregard Robinson (Robinson 1938) a tenté de compléter leur preuve, mais sa démonstration présentait des lacunes, mais elle était si difficile à lire que ces lacunes n'ont pas été remarquées pendant un certain temps et que leur preuve est reproduite dans le livre de Littlewood 1950.

Certaines lacunes ont été comblées ultérieurement dans Macdonald 1995. Les premières démonstrations rigoureuses ont été données quarante ans plus tard par Schützenberger 1977 et Thomas 1974, basées sur la théorie combinatoire développée par Craige Schensted[2], Schützenberger[3], et Knuth[4] dans leurs travaux sur la correspondance de Robinson-Schensted.

Il existe maintenant plusieurs démonstrations brèves, tels que (Gasharov 1998) et (Stembridge 2002) utilisant la notion d'involution de Bender-Knuth (en). Littelmann 1994 utilise le modèle de chemins de Littelmann (en) pour généraliser la règle de Littlewood-Richardson à d'autres groupes de Lie semi-simples.

La règle de Littlewood-Richardson est réputée pour le nombre d'erreurs qui ont pu s'y glisser avant la publication de la première démonstration complète. Même les calculs sont difficiles à mener à bout à la main ; ainsi, même l'exemple original de l'article de Littlewood et Richardson (Littlewood et Richardson 1934) contient une erreur.

Notes et références

Notes

Gordon James, « The representation theory of the symmetric groups », dans The Arcata Conference on Representations of Finite Groups (Arcata, Calif., 1986), Providence, R.I., American Mathematical Society, coll. « Proc. Sympos. Pure Math. » (n^o 47), 1987 (MR 933355), p. 111–126. « Malheureusement, la règle de Littlewood-Richardson et bien plus difficile à démontrer qu'on ne le pensait au début. On a raconté une fois à l'auteur que la règle de Littlewood-Richardson a aidé à envoyer l'homme sur la lune, mais qu'elle n'a pas été démontrée avant ».
Schensted 1961.
Schützenberger 1963.
Knuth 1970.

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Littlewood-Richardson rule » (voir la liste des auteurs).

Références

Ouvrages généraux

William Fulton, Young tableaux, Cambridge University Press, coll. « London Mathematical Society Student Texts » (n^o 35), 1997 (ISBN 978-0-521-56144-0 et 978-0-521-56724-4, MR 1464693).
Ian G. Macdonald, Symmetric functions and Hall polynomials, The Clarendon Press Oxford University Press, coll. « Oxford Mathematical Monographs », 1995, 2^e éd., 475 p. (ISBN 978-0-19-853489-1, MR 1354144, présentation en ligne).
(en) Bruce E. Sagan, The Symmetric Group : Representations, Combinatorial Algorithms, and Symmetric Functions, Springer, coll. « Graduate Texts in Mathematics » (n^o 203), 2001, 2^e éd., 240 p. (ISBN 0-387-95067-2, lire en ligne)

Travaux historiques

Dudley E. Littlewood et Archibald R. Richardson, « Group Characters and Algebra », Philosophical Transactions of the Royal Society of London. Series A, The Royal Society, vol. 233, n^os 721–730,‎ 1934, p. 99–141 (ISSN 0264-3952, DOI 10.1098/rsta.1934.0015, JSTOR 91293, lire en ligne)
Dudley E. Littlewood, The theory of group characters and matrix representations of groups, AMS Chelsea Publishing, Providence, RI, 1950, 310 p. (ISBN 978-0-8218-4067-2, MR 00002127, lire en ligne)
Gilbert de Beauregard Robinson, « On the Representations of the Symmetric Group », American Journal of Mathematics, The Johns Hopkins University Press, vol. 60, n^o 3,‎ 1938, p. 745–760 (ISSN 0002-9327, DOI 10.2307/2371609, JSTOR 2371609) zbMATH: 0019.25102.
Craige Schensted, « Longest increasing and decreasing subsequences », Canadian Journal of Mathematics, vol. 13,‎ 1961, p. 179–191 (ISSN 0008-414X, DOI 10.4153/CJM-1961-015-3, MR 0121305, lire en ligne)
Marcel-Paul Schützenberger, « Quelques remarques sur une construction de Schensted », Mathematica Scandinavica, vol. 12,‎ 1963, p. 117–128 (ISSN 0025-5521, MR 0190017, lire en ligne)
Marcel-Paul Schützenberger, « La correspondance de Robinson », dans Combinatoire et représentation du groupe symétrique (Actes Table Ronde CNRS, Univ. Louis-Pasteur Strasbourg, Strasbourg, 1976), Berlin, New York, Springer-Verlag, coll. « Lecture notes in mathematics » (n^o 579), 1977 (ISBN 978-3-540-08143-2, DOI 10.1007/BFb0090012, MR 0498826, lire en ligne), p. 59–113

Démonstrations de la règle

Vesselin Gasharov, « A short proof of the Littlewood-Richardson rule », European Journal of Combinatorics, vol. 19, n^o 4,‎ 1998, p. 451–453 (ISSN 0195-6698, DOI 10.1006/eujc.1998.0212, MR 1630540, lire en ligne).
John R. Stembridge, « A concise proof of the Littlewood-Richardson rule », Electronic Journal of Combinatorics, vol. 9, n^o 1,‎ 2002, p. 4, article n^o 5 (ISSN 1077-8926, MR 1912814, lire en ligne)

Travaux spécifiques

Donald E. Knuth, « Permutations, matrices, and generalized Young tableaux », Pacific Journal of Mathematics, vol. 34,‎ 1970, p. 709–727 (ISSN 0030-8730, MR 0272654, lire en ligne)
Peter Littelmann, « A Littlewood-Richardson rule for symmetrizable Kac-Moody algebras », Invent. Math., vol. 116,‎ 1994, p. 329–346 (DOI 10.1007/BF01231564, lire en ligne)
Soichi Okada, « Applications of minor summation formulas to rectangular-shaped representations of classical groups », Journal of Algebra, vol. 205, n^o 2,‎ 1998, p. 337–367 (ISSN 0021-8693, DOI 10.1006/jabr.1997.7408, MR 1632816).
Glanffrwd P. Thomas, Baxter algebras and Schur functions, University College of Swansea, coll. « Ph.D. Thesis », 1974.
A. V. Zelevinsky, « A generalization of the Littlewood-Richardson rule and the Robinson-Schensted-Knuth correspondence », Journal of Algebra, vol. 69, n^o 1,‎ 1981, p. 82–94 (ISSN 0021-8693, DOI 10.1016/0021-8693(81)90128-9, MR 613858)

Articles de synthèse

Marc A. A. van Leeuwen, « The Littlewood-Richardson rule, and related combinatorics », dans Interaction of combinatorics and representation theory, Tokyo, Math. Soc. Japan, coll. « MSJ Mem. » (n^o 11), 2001 (MR 1862150, lire en ligne), p. 95–145
Alain Lascoux, Bernard Leclerc et Jean-Yves Thibon, « The plactic monoid », dans M. Lothaire, Algebraic Combinatorics on Words, Cambridge University Press, coll. « Encyclopedia of Mathematics and its Applications » (n^o 90), 2002 (ISBN 978-0-521-81220-7, lire en ligne), p. 164-196

Lien externe

Un programme en ligne pour la décomposition du produit de deux polynômes de Schur d'après la règle de Littlewood-Richardson.

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.