Jeu de taquin de Schützenberger

Les opérations de glissement: ici ${\displaystyle x<y<z}$.

Exemple d'un glissement : 2 glisse dans la cellule vide, 4 monte dans la l'ancienne cellule de 2, et 6 glisse vers la gauche.

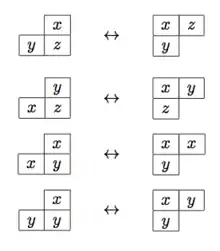
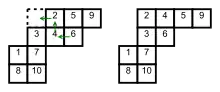
Étant donné un tableau de Young gauche ${\displaystyle T}$ de forme gauche ${\displaystyle \lambda \setminus \mu }$, on choisit une cellule vide ${\displaystyle c}$ adjacente au tableau qui peut être ajoutée au tableau. Cela signifie que ${\displaystyle c}$ a un côté en commun avec une cellule de ${\displaystyle T}$, et que ${\displaystyle \{c\}\cup \lambda \setminus \mu }$ est encore une forme gauche. Il y a deux types de glissements, selon que ${\displaystyle c}$ est dans la partie supérieure gauche, ou dans la partie inférieure droite de ${\displaystyle T}$.

Supposons pour commencer que ${\displaystyle c}$ est dans la partie supérieure gauche. On fait glisser le nombre de la cellule voisine de ${\displaystyle c}$ dans ${\displaystyle c}$ ; si ${\displaystyle c}$ a deux cellules voisines, on prend le plus petit des nombres, et si les nombres sont égaux, la cellule du bas : cette règle assure que la propriété du tableau d'avoir des lignes non décroissantes et des colonnes croissantes est préservée. Si la cellule que l'on vient de vider n'a pas de voisin à droite ou en dessous, le glissement est terminé. Sinon, on fait glisser le nombre de la cellule voisine avec la même règle que précédemment, et on continue jusqu'au bout. À la fin, le tableau obtenu est toujours un tableau de Young (pas nécessairement gauche).

L'autre type de glissement, lorsque ${\displaystyle c}$ est dans la partie inférieure droite de ${\displaystyle T}$, opère de la même manière, mais dans la direction opposée. Dans ce cas, on glisse un nombre dans une cellule vide depuis le voisin de gauche ou de dessus, en prenant le nombre le plus grand des nombres s'il y a un choix. Les deux types de glissements sont l'inverse l'un de l'autre : un glissement d'un des deux types peut être inversé par un glissement le l'autre type.

Le jeu de taquin permet de définir une opération sur les tableaux de Young d'une forme donnée ; cette opération est en fait une involution, même si ce n'est pas évident à partir de la définition. L'opération est la suivante : on commence par vider la cellule supérieure gauche, ce qui transforme le tableau en un tableau gauche. On applique alors un glissement de taquins pour transformer le tableau gauche en un tableau droit. Ceci libère une cellule sur le bord du tableau. Cette cellule est remplie avec l'opposé du nombre qui a été enlevé dans le coin supérieur gauche. Cette valeur négative est considérée comme faisant partie d'un nouveau tableau, et sa position ne changera plus dans la suite. Tant qu'il reste encore des entrées dans le tableau d'origine, on répète l'opération de suppression d'une valeur ${\displaystyle x}$ dans le coin supérieur gauche, de glissement de taquins, et d'insertion de la valeur ${\displaystyle -x}$ dans la cellule libérée. À la fin de ce processus, les valeurs négatives sont réordonnées pour que les lignes et colonnes soient croissantes. Enfin, une constante appropriée est ajoutée à toutes les entrées pour obtenir un tableau de Young à entrées positives.

Tout tableau de Young gauche peut être transformé en un tableau de Young unique par une suite de glissements, donc tout tableau de Young gauche est équivalent à un tableau de Young. L'équivalence définie par les glissements est en fait la même que l'équivalence de Knuth qui définit le monoïde plaxique.

Le jeu de taquin est étroitement lié à la correspondance de Robinson-Schensted-Knuth, et à la règle de Littlewood-Richardson.

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « jeu de taquin » (voir la liste des auteurs).
• (en) Jacques Désarménien, « Jeu de taquin », dans Michiel Hazewinkel, Encyclopædia of Mathematics, Springer, 2002 (ISBN 978-1556080104, lire en ligne)
• (en) Bruce E. Sagan, The Symmetric Group : Representations, Combinatorial Algorithms, and Symmetric Functions, New York/Berlin/Heidelberg etc., Springer, coll. « Graduate Texts in Mathematics » (n^o 203), 2001, 2^e éd., 238 p. (ISBN 0-387-95067-2, lire en ligne)
• Chistophe Reutenauer, « Le jeu de taquin de Schützenberger », La Gazette des Mathématiciens, Société mathématique de France, n^o 116,‎ avril 2008 (lire en ligne, consulté le 14 février 2018).
• Marcel-Paul Schützenberger, « La correspondance de Robinson », dans Dominique Foata (éditeur), Combinatoire et représentation du groupe symétrique : Actes Table Ronde CNRS, Univ. Louis-Pasteur Strasbourg, Strasbourg, 1976, Springer, coll. « Lecture Notes in Math. » (n^o 579), 1977 (ISBN 978-3-540-08143-2, DOI 10.1007/BFb0090012), p. 59–113
• (en) Richard P. Stanley, Enumerative Combinatorics, vol. 2 [détail des éditions] (présentation en ligne)