Octaèdre régulier

Un octaèdre régulier est un octaèdre dont les 8 faces sont des triangles équilatéraux. Il possède 6 sommets et 12 arêtes. C'est un des 5 solides de Platon. C'est aussi un antiprisme triangulaire et une bipyramide carrée. Il possède une sphère circonscrite passant par ses 6 sommets et une sphère inscrite tangente à ses 8 faces.

Octaèdre

**Éléments**
Faces	Arêtes	Sommets
8 triangles équilatéraux	12	6 de degré 4

Données clés
Type	Polyèdre régulier
Références d'indexation	U₀₅ – C₁₇ – W₀₀₂
Symbole de Schläfli	{3,4}
Symbole de Wythoff	4\|2 3
Diagramme C-D
Caractéristique	2
Propriétés	Deltaèdre convexe
Volume (arête $a$ )	${1 \over 3}{\sqrt {2}}a^{3}$
Aire de surface	$2{\sqrt {3}}a^{2}$
Angle dièdre	109,47°
Groupe de symétrie	O_h
Dual	Cube

Comme il a 3 sommets par face, et 4 faces par sommet, son symbole de Schläfli est {3, 4}.

Grandeurs caractéristiques

Si $a$ est la longueur d'une arête :

la distance entre 2 sommets opposés est : ${\sqrt {2}}\,a$ ;
le rayon de sa sphère circonscrite est : $R={\frac {a}{\sqrt {2}}}$ ;
son angle dihédral est $\arccos \left(-{\frac {1}{3}}\right)\approx 109{,}47^{\circ }$ ;
le rayon de sa sphère inscrite est : $r={\frac {a}{\sqrt {6}}}$ ;
son aire est : $A=2{\sqrt {3}}_{,}a^{2}$ ;
son volume est : $V={\frac {\sqrt {2}}{3}}\,a^{3}$ ;
les 6 points de coordonnées cartésiennes $(\pm {\frac {a}{\sqrt {2}}},0,0)$ , $(0,\pm {\frac {a}{\sqrt {2}}},0)$ et $(0,0,\pm {\frac {a}{\sqrt {2}}})$ sont les sommets d'un octaèdre régulier centré sur l'origine.

Propriétés diverses

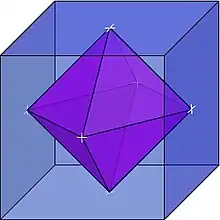
Octaèdre régulier inscrit dans un cube. Cette figure montre que ces deux polyèdres sont duaux l'un de l'autre.

L'octaèdre et le cube sont duaux l'un de l'autre, c'est-à-dire que le polyèdre ayant pour sommets les centres des faces de l'un est homothétique de l'autre.

Le squelette de l'octaèdre régulier, c'est-à-dire l'ensemble de ses sommets reliés par ses arêtes, forme un graphe appelé graphe octaédrique.

Patron de l'octaèdre régulier

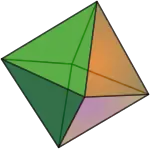
Platon l'associait à l'élément naturel « air »[1].

Exemples

Dans les jeux

L'octaèdre régulier est utilisé comme dé à jouer, particulièrement dans les jeux de rôle.

En cristallographie

Certains cristaux comme la fluorine forment un octaèdre régulier.

En chimie

Certaines molécules peuvent avoir une géométrie moléculaire octaédrique.

Généralisation

L'hyperoctaèdre, ou n-octaèdre, est la généralisation de l'octaèdre en n dimensions.

L'hyperoctaèdre est, avec son dual l'hypercube et le n-simplexe, un des trois seuls polytopes existant sous forme régulière dans toute dimension n. Les polytopes réguliers sont en effet une infinité en dimension 2 (voir polygone régulier), 5 en dimension 3 (voir solide de Platon), 6 en dimension 4, et après ils ne sont plus que 3, comme Ludwig Schläfli l'a démontré.

Le symbole de Schläfli d'un n-octaèdre est de la forme {3, 3, 3, … , 3, 4} avec n – 1 chiffres.

Les coordonnées des sommets d'un hyperoctaèdre centré à l'origine sont obtenues en permutant les coordonnées (±1, 0, 0, … , 0, 0).

Les premiers hyperoctaèdres
Hyperoctaèdre	Carré	Octaèdre	Hexadécachore ou 16-cellules	5-octaèdre
Dimension	2	3	4	5
Sommets	4	6	8	10
Représentation

Hypervolume d'un hyperoctaèdre régulier

L'hypervolume d'un polytope est le contenu n-dimensionnel de ce polytope. Soit a son arête.

Pour construire un (n + 1)-octaèdre, on relie les 2n sommets d'un n-octaèdre à un nouveau point au-dessus et à un nouveau point au-dessous.

Ainsi, un segment dont les extrémités sont reliées à un point au-dessus et à un point au-dessous donne un carré (on supposera que les points ont été placés de sorte à donner un hyperoctaèdre régulier).
Un carré dont les sommets sont reliés à un point au-dessus et à un point au-dessous donne un octaèdre.
Un octaèdre dont les sommets sont reliés à un point au-dessus et à un point en dessous (situés dans une autre dimension) donne bien un hexadécachore.

L'hyperoctaèdre est donc une double hyperpyramide (à base hyperoctaédrique de dimension inférieure). Étant régulier dans le cas étudié, ses sommets sont tous sur une n-sphère circonscrite. Cette n-sphère circonscrite est également celle de ses faces hyperoctaédriques de dimensions inférieures, car tous les sommets de l'hyperoctaèdre régulier sont dessus. Le rayon du centre de cette n-sphère aux sommets est donc le même pour toute dimension n : $R_{n}={\frac {a{\sqrt {2}}}{2}}$ .

L'hypervolume est celui de deux hyper-pyramides de hauteur $R_{n}$ . On en déduit donc que l'hypervolume (le n-contenu) d'un n-octaèdre régulier d'arête a vaut :

$V_{n}={\frac {V_{n-1}\times R_{n}}{n}}\times 2={\frac {(a{\sqrt {2}})^{n}}{n!}}$ .

Exemples :

Aire du carré : $V_{2}={\frac {(a{\sqrt {2}})^{2}}{1\times 2}}=a^{2}$
Volume de l'octaèdre régulier : $V_{3}={\frac {(a{\sqrt {2}})^{3}}{1\times 2\times 3}}={\frac {a^{3}{\sqrt {2}}}{3}}$ ;
Hypervolume de l'hexadécachore : $V_{4}={\frac {(a{\sqrt {2}})^{4}}{1\times 2\times 3\times 4}}={\frac {a^{4}}{6}}$ ;
…

(On suppose dans cette formule que le seul n-octaèdre à ne pas avoir une longueur d'arête égale à a est le segment (1-octaèdre), qui a dans ce cas pour longueur $a{\sqrt {2}}$ (diagonale d'un carré) pour donner bien un carré de côté a avec la méthode de construction donnée)

Notes et références

Les cinq éléments de Platon : Histoire du solide de Platon

Cet article est partiellement ou en totalité issu de l'article intitulé « Octaèdre » (voir la liste des auteurs).

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.