Géométrie moléculaire octaédrique

En chimie, une géométrie moléculaire octaédrique est la géométrie des molécules où un atome central, noté A, est lié à six atomes, groupe d'atomes ou ligands, notés X, formant un octaèdre régulier. Cette configuration est notée AX₆E₀ selon la théorie VSEPR.

Géométrie moléculaire octaédrique

Notation VSEPR	AX₆E₀ (AX₆)
Exemple(s)	SF₆, Mo(CO)₆
Symétrie moléculaire	O_h
Nombre stérique	6
Coordinence	6
Doublet non liant	0
Angle de liaison	90°

Structure de l'hexafluorure de soufre, un exemple de molécule avec une géométrie moléculaire octaédrique.

Les angles de liaison sont de 90° lorsque tous les substituants sont les mêmes, et la structure est alors un octaèdre parfait appartenant au groupe ponctuel de symétrie O_h. C'est par exemple le cas avec l'hexafluorure de soufre (SF₆) ou avec l'hexacarbonyle de molybdène (Mo(CO)₆), mais la plupart des molécules octaédriques ne possèdent pas une si forte symétrie.

Le terme « octaédrique » est utilisé de façon peu rigoureuse par les chimistes qui se focalisent sur la géométrie des liaisons vers l'atome central, sans considérer les différences entre les ligands. Par exemple, le complexe d'hexaminecobalt(III) ([Co(NH₃)₆]³⁺) n'est pas octaédrique au sens mathématique du terme, du fait de l'orientation des liaisons N-H, mais il est tout de même considéré en chimie comme ayant une géométrie octaédrique[1].

Le concept de géométrie de coordination octaédrique fut développé par le chimiste suisse Alfred Werner, afin d'expliquer les stœchiométries et isoméries dans les complexes. Son intuition a permis aux chimistes de rationaliser le nombre d'isomères des complexes. Son nom est par ailleurs associé aux complexes octaédriques de métaux de transition contenant des amines et des anions simples, souvent appelés de « type Werner ».

Géométrie moléculaire bi-octaédrique

Une structure bi-octaédrique est une structure dans laquelle une arête de l'octaèdre est partagée par deux sous-structures octaédriques. De nombreux pentahalogénures et pentalcoolates de métaux existent en solution, où le solide a une structure bi-octaédrique. Parmi eux, on peut citer le pentachlorure de niobium. Des tétrahalogénures des métaux existent souvent à l'état de polymères constitué d'unités octaédriques partageant leurs arêtes ; c'est par exemple le cas du tétrachlorure de zirconium[2].

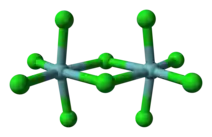Modèle ball-and-stick du pentachlorure de niobium.
Modèle ball-and-stick du tétrachlorure de zirconium.

Isomérie dans les complexes octaédriques

Lorsque deux types de ligands ou plus (L^a, L^b, etc.) sont complexés avec une métal (M) dans une structure octaédrique, ce complexe peut exister sous la forme de plusieurs isomères. La nomenclature de tels isomères dépend du nombre et de la position de ces différents ligands.

Isomères cis et trans

Pour un complexe de type ML^a₄L^b₂ (un quadruplet et une paire de ligands identiques), il existe deux isomères. Si les ligands L^b sont situés de part et d'autre du métal central (angle L^b-M-L^b de 180°), l'isomère est qualifié de trans. Dans le cas contraire, où les ligands L^b sont mutuellement adjacents (angle L^b-M-L^b de 90°), il est qualifié de cis.

trans-[CoCl₂(NH₃)₄]⁺
cis-[CoCl₂(NH₃)₄]⁺

Ce sont les travaux sur de tels complexes, et le postulat qu'ils avaient une structure octaédriques qui valurent à Alfred Werner le prix Nobel de chimie en 1913.

Isomères faciaux et méridionaux

Pour un complexe de type ML^a₃L^b₃ (deux triplets de ligands identiques), il existe deux isomères. Si deux des trois ligands identiques (L^a ou L^b) sont trans (de part et d'autre de l'atome central) et que donc les trois ligands sont sur un même plan passant par le centre métallique, l'isomère est qualifié de « méridional » (mer). Si au contraire ces trois ligands sont tous mutuellement cis, et sont donc les trois sommets d'une face de l'octaèdre, l'isomère est qualifié de « facial » (fac). Alterntivement, l'isomère méridional peut être vu comme l'isomère où chacun des deux plans contenant un triplet de ligands identiques passe également par l'atome central (et les deux plans sont perpendiculaires), et l'isomère facial celui pour lequel de tels plans ne passent pas par l'atome central (et les plans sont parallèles).

mer-[CoCl₃(NH₃)₃]
fac-[CoCl₃(NH₃)₃]

Cas général de la stéréochimie en série octaédrique

Si l'isomérie cis-trans et fac-mer couvre complètement le complexes possédant deux ligands différents, il existe de nombreux complexes qui en possède plus de deux. Leur nomenclature est prévue par les règles de l'IUPAC. La configuration du complexe est du type (OC-6-xy) ou x et y sont deux nombres entiers appelés "indice de configuration" définis par les règles suivantes [3]:

La priorité des ligands est donnée, à partir de l'atome lié au métal, par les règles de Cahn, Ingold et Prelog. Chaque ligand possède ainsi un numéro de priorité.
Le premier indice de configuration est le numéro de priorité de l'atome lié au métal en position trans de l'atome lié au métal avec un numéro de priorité 1.
S'il y a plus d'un atome de priorité 1, le premier indice de configuration est le numéro de priorité du ligand trans avec la valeur numérique la plus élevée (atome le moins prioritaire).
On se souvient également que les valeurs qui ont des primes (par exemple 3’) sont considérées comme étant des valeurs supérieures à la valeur correspondant qui n’a pas de prime. On considère ainsi que 3’ > 3. [les primes sont utilisés pour marquer les ligands polydentates identiques]
Ces deux atomes considérés : l'atome de priorité 1 et l’atome (de priorité la plus basse) en trans de celui-ci, définissent l'axe de référence de l'octaèdre.
Le deuxième chiffre de l'indice de configuration est le numéro de priorité de l'atome lié au métal en trans par rapport à l'atome lié au métal de plus grande priorité (de plus petite valeur numérique) dans le plan perpendiculaire à l’axe de référence de l’octaèdre.
S'il y a plus d'un tel atome de même priorité dans ce plan, l’index de configuration est le numéro de priorité de l’atome trans ayant la plus grande valeur numérique (priorité moindre).

Chiralité

Des complexes plus compliqués, avec plus de deux types de ligands, ou des ligands bidentate peuvent aussi être chiraux, avec des paires d'isomères énantiomères (images l'un de l'autre dans un miroir, non-superposables).

Λ-[Fe(ox)₃]³⁻
Δ-[Fe(ox)₃]³⁻
Λ-cis-[CoCl₂(en)₂]⁺
Δ-cis-[CoCl₂(en)₂]⁺

Autres

Pour un complexe de type ML^a₂L^b₂L^c₂ (trois paires de ligands identiques), six isomères sont possibles[4] :

un isomère dans lequel chacune des trois paires de ligands identiques sont en position trans ;
trois isomères distincts dans lesquels une paire de ligands identiques (L^a ou L^b ou L^c) est en position trans quand les autres sont en position cis ;
deux énantiomères chiraux dans lesquels toutes les paires de ligands identiques sont en position cis.

Le tableau ci-dessous résume le nombre d'isomères possibles en fonction des ligands possibles.

Formule	Nombre d'isomères	Nombre de paire d'énantiomères
ML₆	1	0
ML^a₅L^b	1	0
ML^a₄L^b₂	2	0
ML^a₄L^bL^c	2	0
ML^a₃L^b₃	2	0
ML^a₃L^b₂L^c	3	0
ML^a₃L^bL^cL^d	5	1
ML^a₂L^b₂L^c₂	6	1
ML^a₂L^b₂L^cL^d	8	2
ML^a₂L^bL^cL^dL^e	15	6
ML^aL^bL^cL^dL^eL^f	30	15

Ainsi, tous les 15 diastéréoisomères de ML^aL^bL^cL^dL^eL^f sont chiraux, quand pour ML^a₂L^bL^cL^dL^e, 6 diastéréoisomères le sont et 3 ne le sont pas, ceux où les ligands L^a sont en position trans. Pour un complexe avec six ligands différents, le nombre d'isomères possible est de 30. Par comparaison, un complexe tétraédrique avec quatre ligands différents ne possède que deux stéréoisomères.

On voit ainsi que la chimie de coordination octaédrique offre une bien plus grande complexité que la tétraédrique, qui est majoritaire en chimie organique.

Géométrie prismatique trigonale

Pour les composés de formule MX₆, la principale géométrie « concurrente » à la géométrie octaédrique est la géométrie prismatique trigonale, avec une symétrie D_3h. Dans cette géométrie, les six ligands jouent aussi un rôle équivalent. Il existe aussi des prismes trigonaux, avec une symétrie C_3v ; on peut citer parmi les composés adoptant cette géométrie l'hexaméthyltungstène (W(CH₃)₆). On pense que l'interconversion des complexes Δ et Λ, qui est d'ordinaire lente, se produit via un intermédiaire prismatique trigonal, dans un procédé appelé « torsion de Bailar (en) ». Une autre voie possible pour la racémisation de tels complexes est la torsion de Ray-Dutt (en).

Levée de dégénérescence partielle des orbitales d dans les complexes octaédriques

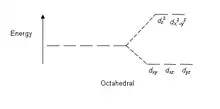
Levée de dégénérescence partielle des orbitales d dans un système octaédriques. Les 5 orbitales d initialement de même énergie se retrouvent séparées en deux groupes, deux déstabilisées avec une énergie e_g, trois stabilisées avec une énergie t_2g.

Pour un « ion libre », par exemple Ni²⁺ ou Mo⁰ gazeux, les orbitales d sont « dégénérées », c'est-à-dire qu'elles ont toutes la même énergie. Dans les complexes octaédriques, cette dégénérescence est partiellement levée : les orbitales d_z² et d_x²−y², qui pointent directement vers les ligands sont déstabilisées et voient donc leur énergie augmentée au niveau e_g. Au contraire, les orbitales d_xz, d_xy et d_yz sont stabilisées et voient leur énergie réduites au niveau t_2g. Ces orbitales restent donc partiellement dégénérées, avec respectivement deux et trois orbitales partageant la même énergie. La différence d'énergie entre les deux groupes (eg-t_2g) est notée Δ_o, et elle varie selon le nombre et la nature des ligands. Si la symétrie du complexe est plus basse que celle du système octaédrique parfait, les niveaux e_g et t_2g peuvent se séparer de nouveau. C'est par exemple le cas pour les composés de type trans-ML^a₄L^b₂.

Cette séparation des orbitales d en deux groupes et la différence d'énergie entre les deux nouveaux niveaux d'énergie est à la base de la théorie du champ cristallin ainsi que de la théorie du champ de ligands.

On mesure la « force » des ligands en fonction de l'énergie Δ_o de séparation qu'ils provoquent ; un ligand faible donnera une énergie Δ_o faible, et le composé absorbera des longueurs d'onde plus grandes. On classe les ligands donneurs d'électrons comme suit :

faible : iode < brome < fluor < acétate < oxalate < eau < pyridine < carbonyle : fort

Réactions

Du fait du nombre presque illimité de différents complexes octaédriques pouvant exister, il existe un grand nombre de réactions les concernant. Ces réactions peuvent être classées en différents catégories :

réactions de substitution de ligand (via de nombreux mécanismes) ;
réactions d'addition de ligand, et parmi beaucoup d'autres, la protonation ;
réactions rédox (pertes ou gains d'électrons)
réarrangements ou la stéréochimie relative du ligand change dans la sphère de coordination.

Beaucoup de réaction des complexes octaédriques de métaux de transition se passent dans l'eau. Lorsque des ligands anioniques remplacent un ligand eau, on parle d'« anation ». La réaction inverse, l'eau remplaçant un ligand anionique, est appelée « aquation ». Par exemple, le complexe [CoCl(NH₃)₅]²⁺ s'aquate lentement en [Co(NH₃)₅(H₂O)]³⁺ dans l'eau, en particulier en présence d'acide ou de base. L'ajout d'acide chlorhydrique concentré reconvertit le complexe aquo en chlorure, par anation.

Notes et références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Octahedral molecular geometry » (voir la liste des auteurs).

von Zelewsky, A. "Stereochemistry of Coordination Compounds" John Wiley: Chichester, 1995. (ISBN 0-471-95599-X).
Wells, A.F. (1984) Structural Inorganic Chemistry, Oxford: Clarendon Press. (ISBN 0-19-855370-6).
https://www.iupac.org/fileadmin/user_upload/databases/Red_Book_2005.pdf Texte traduit de la section IR-9.3.3.4
Miessler G.L. and Tarr D.A. Inorganic Chemistry (2nd ed. Prentice-Hall 1999) p.290

Voir aussi

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.