Diagramme de Coxeter-Dynkin
En géométrie, un diagramme de Coxeter-Dynkin est un graphe représentant un ensemble relationnel de miroirs (ou d'hyperplans de réflexion) dans l'espace pour une construction kaléidoscopique.
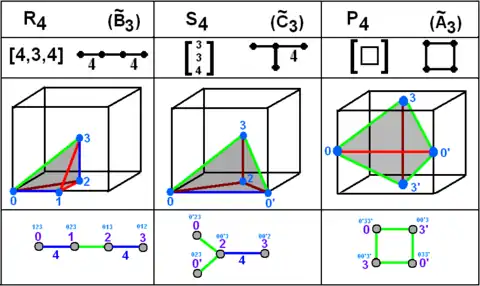
R4 remplit 1/24 du cube. S4 remplit 1/12 du cube. P4 remplit 1/6 du cube.
En tant que graphe lui-même, le diagramme représente les groupes de Coxeter, chaque nœud du graphe représente un miroir (facette du domaine) et chaque branche du graphe représente l'ordre de l'angle diédral entre deux miroirs (sur une arête du domaine).
En plus, les graphes ont des anneaux (cercles) autour des nœuds pour les miroirs actifs représentant un polytope uniforme (en) précis.
Le diagramme est issu du diagramme de Dynkin.
Description
Le diagramme peut aussi représenter les polytopes en ajoutant des anneaux (des cercles) autour des nœuds. Chaque diagramme doit avoir au moins un nœud actif pour représenter un polytope.
Les anneaux expriment une information : si un point générateur est dans ou en dehors du miroir. Plus précisément, un miroir est actif (il crée des réflexions) seulement lorsque des points sont en dehors du miroir, donc ajouter un anneau signifie qu'un point est en dehors du miroir et crée une réflexion.
Les arêtes sont étiquetées avec un entier naturel n représentant un angle diédral de 180/n. Si une arête n'est pas étiquetée, elle est supposée être 3. Si n=2, l'angle est 90 degrés et les miroirs n'ont pas d'interaction, et l'arête peut être omise. Deux miroirs parallèles peuvent être marqués avec « ∞ ».
En principe, n miroirs peuvent être représentés par un graphe complet dans lequel toutes les n*(n-1)/2 sont dessinées. En pratique, les configurations intéressantes de miroirs incluront un nombre d'angles droits, et les arêtes correspondantes peuvent être omises.
Les polytopes et les pavages peuvent être engendrés en utilisant ces miroirs et un point générateur unique. Les images miroir créent des nouveaux points comme réflexions. Les arêtes peuvent être créées entre les points et une image miroir. Les faces peuvent être construites par cycles d'arêtes créées, etc.
Exemples
- Un nœud unique représente un miroir unique. Ceci est appelé le groupe A1. S'il est annelé, il crée un digone ou une arête perpendiculaire au miroir, représenté par {} ou {2}.
- Deux nœuds non attachés représentent deux miroirs perpendiculaires. Si les deux nœuds sont annelés, un rectangle peut être créé ou un carré si le point est à égale distance des deux miroirs.
- Deux nœuds attachés par une arête d'ordre n peut créer un n-gone si le point est sur un miroir, et un 2n-gone si le point est en dehors des deux miroirs. Ceci forme le groupe D2n.
- Deux miroirs parallèles peuvent représenter un groupe de polygone infini D2∞, aussi appelé W2.
- Trois miroirs dans un triangle forment des images vues dans un kaléidoscope traditionnel et sont représentées par 3 nœuds attachés dans un triangle. En répétant les exemples auront des arêtes étiquetées comme (3 3 3), (2 4 4), (2 3 6), bien que les deux derniers peuvent être dessinés dans une droite avec l'arête 2 ignorée. Ceux-ci engendreront les pavages uniformes.
- Trois miroirs peuvent engendrer les polyèdres uniformes, incluant les nombres rationnels est l'ensemble des triangles de Schwarz (en).
- Trois miroirs avec un perpendiculaire aux deux autres peuvent former les prismes uniformes.
En général, tous les n-polytopes réguliers, représentés par le symbole de Schläfli {p,q,r,...} peuvent avoir leur domaines fondamentaux représentés par un ensemble de n miroirs et sont reliés dans un diagramme de Coxeter-Dynkin dans une droite de nœuds et d'arêtes étiquetées par p,q,r...
Groupes finis de Coxeter
Les familles de polytopes convexes uniformes sont définis par les groupes de Coxeter.
Notes :
- Trois symboles différents sont donnés pour les mêmes groupes - une lettre/nombre, un ensemble de nombres avec des accolades et le diagramme de Coxeter.
- Les groupes bifurqués Bn sont aussi donnés par la notation h[] représentant le fait que c'est une version demie ou alternée des groupes réguliers Cn.
- Les groupes bifurqués Bn et En sont aussi étiquetés par un exposant [3a,b,c] où a,b,c sont le nombre de segments dans chacune des 3 branches.
| n | A1+ | B4+ | C2+ | D2p | E6-8 | F4 | G2-4 |
|---|---|---|---|---|---|---|---|
| 1 | A1=[] |
||||||
| 2 | A2=[3] |
C2=[4] |
D2p=[p] |
G2=[5] | |||
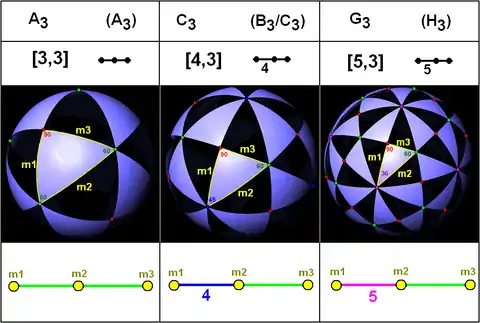
| 3 | A3=[3²] |
B3=A3=[30,1,1] |
C3=[4,3] |
G3=[5,3] | |||
| 4 | A4=[3³] |
B4=h[4,3,3]=[31,1,1] |
C4=[4,3²] |
E4=A4=[30,2,1] |
F4=[3,4,3] |
G4=[5,3,3] | |
| 5 | A5=[34] |
B5=h[4,3³]=[32,1,1] |
C5=[4,3³] |
E5=B5=[31,2,1] |
|||
| 6 | A6=[35] |
B6=h[4,34]=[33,1,1] |
C6=[4,34] |
E6=[32,2,1] |
|||
| 7 | A7=[36] |
B7=h[4,35]=[34,1,1] |
C7=[4,35] |
E7=[33,2,1] |
|||
| 8 | A8=[37] |
B8=h[4,36]=[35,1,1] |
C8=[4,36] |
E8=[34,2,1] |
|||
| 9 | A9=[38] |
B9=h[4,37]=[36,1,1] |
C9=[4,37] |
||||
| 10+ | .. | .. | .. | .. | .. | .. | .. |
(Note : les noms alternatifs comme les groupes de Lie simples (en) sont donnés.)
- An forme la famille des polytopes simpliciaux (même nom : An).
- Bn est la famille des demi-hypercubes, commençant à n=4 avec le 24-cellules et n = 5 avec le penteract (aussi nommé Dn).
- Cn forme la famille des hypercubes (même nom : Cn).
- D2n forme les polygones réguliers (aussi nommé I1n).
- E6,E7,E8 sont les générateurs des polytopes semi-réguliers de Gosset (mêmes noms : E6,E7,E8).
- F4 est la famille du polychore 24-cellules (même nom : F4).
- G3 est la famille du polyèdre dodécaèdre/icosaèdre (aussi nommé H3).
- G4 est la famille du polychore 120-cellules/600-cellules (aussi nommé H4).
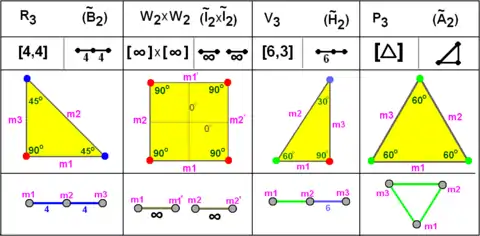
Les groupes de Coxeter infinis
Les familles de pavages uniformes convexes sont définis par les groupes de Coxeter.
Notes :
- Les groupes réguliers (linéaires) peuvent être donnés avec une notation équivalente avec des accolades.
- Le groupe Sn peut aussi être étiqueté par une notation h[] comme une moitié d'un régulier.
- Le groupe Qn peut aussi être étiqueté par une notation q[] comme un quart d'un régulier.
- Les groupes bifurqués Tn sont aussi étiquetés par une forme exposant [3a,b,c] où a,b,c sont le nombre de segments dans chacune des 3 branches.
| n | P3+ | Q5+ | R3+ | S4+ | T7-9 | U5 | V3 | W2 |
|---|---|---|---|---|---|---|---|---|
| 2 | W2=[∞] | |||||||
| 3 | P3=h[6,3] |
R3=[4,4] |
V3=[6,3] |
|||||
| 4 | P4=q[4,3,4] |
R4=[4,3,4] |
S4=h[4,3,4] |
|||||
| 5 | P5 |
Q5=q[4,3²,4] |
R5=[4,3²,4] |
S5=h[4,3²,4] |
U5=[3,4,3,3] |
|||
| 6 | P6 |
Q6=q[4,3³,4] |
R6=[4,3³,4] |
S6=h[4,3³,4] |
||||
| 7 | P7 |
Q7=q[4,34,4] |
R7=[4,34,4] |
S7=h[4,34,4] |
T7=[32,2,2] |
|||
| 8 | P8 |
Q8=q[4,35,4] |
R8=[4,35,4] |
S8=h[4,35,4] |
T8=[33,3,1] |
|||
| 9 | P9 |
Q9=q[4,36,4] |
R9=[4,36,4] |
S9=h[4,36,4] |
T9=[35,2,1] |
|||
| 10 | P10 |
Q10=q[4,37,4] |
R10=[4,37,4] |
S10=h[4,37,4] |
||||
| 11 | ... | ... | ... | ... |
(Note : les noms alternatifs comme les groupes de Lie simples sont aussi donnés.)
- Pn est un groupe cyclique (aussi nommé ~An-1).
- Qn (aussi nommé ~Dn-1)
- Rn forme la famille de pavage régulier de l'hypercube {4,3,....} (aussi nommé ~Bn-1).
- Sn forme la famille de pavage alternée hypercubique (aussi nommé ~Cn-1).
- T7,T8,T9 sont les pavages de Gosset (aussi nommés ~E6,~E7,~E7).
- U5 est le pavage régulier du 24-cellules {3,4,3,3} (aussi nommé ~F4).
- V3 est le pavage hexagonal (aussi nommé ~H2).
- W2 est composé de deux miroirs parallèles (aussi nommé ~I1).
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Coxeter–Dynkin diagram » (voir la liste des auteurs).
- (en) Kaleidoscopes: Selected Writings of H.S.M. Coxeter, editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience, 1995 (ISBN 978-0-471-01003-6), paper 17 : The Evolution of Coxeter-Dynkin diagrams, [Nieuw Archief voor Wiskunde 9 (1991) 233-248]
- (en) H. S. M. Coxeter, The Beauty of Geometry: Twelve Essays, Dover, 1999 (ISBN 978-0-486-40919-1) (Chapter 3: Wythoff's Construction for Uniform Polytopes)
- (en) H. S. M. Coxeter, Regular Polytopes (Macmillian, 1963), 3e éd., Dover, 1973 (ISBN 0-486-61480-8) (Chapter 5: The Kaleidoscope, and Section 11.3 Representation by graphs)
Voir aussi
Articles connexes
- Symbole de Wythoff
- Liste des polyèdres uniformes
- Liste des pavages uniformes (en)
- 4-polytope uniforme
- Nid d'abeille uniforme convexe (en)
- Construction de Wythoff
Lien externe
(en) [PDF] Regular Polytopes, Root Lattices, and Quasicrystals, R. Bruce King