Matrice des degrés

Étant donné un graphe ${\displaystyle G=(V,E)}$ contenant ${\displaystyle n}$ sommets, la matrice des degrés ${\displaystyle D}$ de ${\displaystyle G}$ est la matrice carrée ${\displaystyle n\times n}$ définie par :

${\displaystyle D_{i,j}:=\left\{{\begin{matrix}\deg(v_{i})&{\mbox{si}}\ i=j\\0&{\mbox{sinon}}\end{matrix}}\right.}$.

Le degré du sommet est le nombre de liens (arêtes ou arcs) aboutissant à ce sommet. Ainsi, pour un graphe non orienté, chaque boucle compte pour 2 : en effet, chaque lien a deux extrémités et chacune de ces deux extrémités augmente le degré. De la même façon, les sommets isolés ont un degré égal à 0.

Dans le cas d'un graphe orienté, le degré d'un sommet est la somme de son degré entrant et de son degré sortant[1].

Graphe étiqueté	Matrice des degrés
	${\displaystyle {\begin{pmatrix}4&0&0&0&0&0\\0&3&0&0&0&0\\0&0&2&0&0&0\\0&0&0&3&0&0\\0&0&0&0&3&0\\0&0&0&0&0&1\\\end{pmatrix}}}$

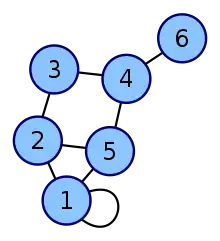Le degré du sommet 1 vaut 4 : en effet, le sommet 1 est connecté aux sommets 2 et 5, et il y a aussi la boucle. Ainsi, le sommet 1 est de degré 2+2 = 4.

Le degré du sommet 2 vaut 3 : en effet, le sommet numéro 2 est connecté aux sommet 1, 3 et 5, d'où un degré de 3.

Graphe de Petersen : graphe régulier où les sommets de degré 3.

La matrice des degrés d'un graphe régulier de degré ${\displaystyle k}$ a une diagonale dont les coefficients valent tous ${\displaystyle k}$. Par exemple pour le graphe de Peterson (voir Figure), qui possède 10 noeuds, la matrice des degrés est de taille 10 X 10 et contient que des 3 sur la diagonale :

${\displaystyle {\begin{pmatrix}3&0&0&0&0&0&0&0&0&0\\0&3&0&0&0&0&0&0&0&0\\0&0&3&0&0&0&0&0&0&0\\0&0&0&3&0&0&0&0&0&0\\0&0&0&0&3&0&0&0&0&0\\0&0&0&0&0&3&0&0&0&0\\0&0&0&0&0&0&3&0&0&0\\0&0&0&0&0&0&0&3&0&0\\0&0&0&0&0&0&0&0&3&0\\0&0&0&0&0&0&0&0&0&3\end{pmatrix}}}$