Hypercube (graphe)
Les hypercubes, ou n-cubes, forment une famille de graphes. Dans un hypercube , chaque sommet porte une étiquette de longueur sur un alphabet , et deux sommets sont adjacents si leurs étiquettes ne diffèrent que d'un symbole. C'est le graphe squelette de l'hypercube, un polytope n-dimensionnel, généralisant la notion de carré (n = 2) et de cube (n = 3). Dans les années 1980, des ordinateurs furent réalisés avec plusieurs processeurs connectés selon un hypercube : chaque processeur traite une partie des données et ainsi les données sont traitées par plusieurs processeurs à la fois, ce qui constitue un calcul parallèle. L'hypercube est couramment introduit pour illustrer des algorithmes parallèles, et de nombreuses variantes ont été proposées, soit pour des cas pratiques liés à la construction de machines parallèles, soit comme objets théoriques.
| Hypercube | |
 Q4 | |
| Notation | Qn ou Hn |
|---|---|
| Nombre de sommets | 2n |
| Nombre d'arêtes | 2n-1n |
| Distribution des degrés | n-régulier |
| Diamètre | n |
| Maille | 4 |
| Coefficient de clustering | 0 |
| Automorphismes | 2nn! |
| Nombre chromatique | 2 |
| Propriétés | Hamiltonien Distance-unité Graphe de Cayley Symétrique Distance-régulier |
| Utilisation | Machines parallèles |
Construction
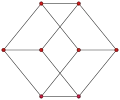
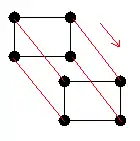
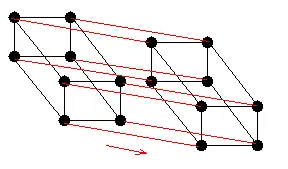
L'hypercube consiste en deux sommets d'étiquettes et ; les étiquettes de ces sommets étant différentes par un seul symbole, ils sont donc reliés. Pour passer à la dimension supérieure, on fabrique une copie du graphe : à la partie d'origine, on rajoute le symbole , et sur la partie copiée le symbole ; chaque sommet de la partie d'origine est ensuite relié à son équivalent dans la copie. Ainsi, consiste en quatre sommets étiquetés , , et . L'illustration ci-dessous montre en rouge les arêtes connectant les sommets d'origine à leurs équivalents dans la copie, et l'exemple se poursuit jusqu'à et . Cette méthode de construction est récursive, puisque pour construire on se fonde sur .
![]() →
→
 →
→
 →
→
On peut aussi définir comme le produit cartésien[A 1] de graphes complets , soit :
Enfin, on peut construire le graphe directement en appliquant sa définition. On dispose sommets, et chacun a une étiquette unique dans l'espace vectoriel[D 1] , c'est-à-dire une étiquette de la forme . Deux sommets sont reliés par une arête s'ils diffèrent exactement sur un symbole de leurs étiquettes, soit formellement pour le graphe :
Le graphe hypercube est le graphe hexaédrique et est le graphe tesseract.
Propriétés
Fondamentales
- Degré. Deux sommets sont connectés s'ils diffèrent exactement sur un symbole de leurs étiquettes. Comme l'étiquette a symboles, chaque sommet est connecté à exactement voisins : tout sommet a donc degré , autrement dit le graphe est -régulier.
- Nombre de sommets. Par la construction récursive, on voit que pour passer de à , il faut faire une copie du graphe, autrement dit le nombre de sommets est doublé. Si est le nombre de sommets du graphe , on obtient ainsi , et le premier cas est ; en déroulant la récurrence, on obtient , c'est-à-dire que le graphe a sommets.
- Diamètre[A 1]. Une des propriétés du produit cartésien est que le diamètre de est égal à . Comme est le produit cartésien de graphes complets , son diamètre est égal à .

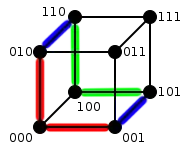
- Cycles. Par construction, le plus petit cycle correspond à , qui est isomorphe au cycle (i.e. le cycle de longueur 4). Le graphe est formé par deux graphes : si l'on souhaite un cycle de longueur supérieur à 4 dans , alors on choisit arêtes dans un des deux graphes , arêtes dans l'autre et 2 arêtes supplémentaires pour naviguer entre les deux graphes, ce qui porte le total d'arêtes à ; ce mécanisme est illustré dans la figure ci-contre avec un cycle de longueur 6, et permet de prouver que les cycles dans un hypercube sont toujours de longueur paire.
- Nombre chromatique. Un graphe est biparti si et seulement s'il ne contient pas de cycle impair, et il découle donc de la propriété précédente que l'hypercube est biparti. Un graphe biparti est celui pouvant être colorié avec deux couleurs, et ainsi le nombre chromatique de l'hypercube est . Pour voir qu'un graphe est biparti, il suffit de trouver un schéma afin de ranger chaque sommet dans un ensemble ou , de façon telle que tout sommet d'un ensemble ait comme voisins uniquement des sommets de l'autre ensemble. Dans le cas de l'hypercube[D 2], l'ensemble peut être constitué des sommets dont l'étiquette a un nombre pair de 1, et est l'ensemble de sommets dont l'étiquette a un nombre impair de 1. Un sommet étant connecté à tous ceux dont l'étiquette diffère exactement d'un symbole, il en découle que le nombre de 1 des voisins d'un sommet est soit supérieur soit inférieur : ainsi, un sommet pair sera connecté à des sommets impairs, et vice-versa.
- Planaire. L'hypercube est planaire (c'est-à-dire pouvant se dessiner sur un plan sans croiser deux arêtes) uniquement pour . Pour , plusieurs arêtes vont se croiser mais déterminer le nombre minimum d'arêtes qui vont se croiser est un problème NP-complet[D 2] ; on sait par exemple qu'il y en a 8 pour .
- Eulérien. Un graphe a un chemin eulérien si et seulement si tout sommet est de degré pair. Comme est -régulier, il en résulte qu'il n'y a un chemin eulérien que pour pair.
- Hamiltonien. étant un cycle, il est aussi un circuit hamiltonien. Pour construire un circuit hamiltonien dans , on sait qu'il y a un circuit hamiltonien dans le graphe d'origine et dans sa copie : supprimons une arête dans chacun de ces circuits et raccordons les sommets ainsi libérés pour créer un circuit hamiltonien dans l'ensemble. Ce processus est illustré ci-dessous pour et . Le nombre exact de cycles hamiltoniens est donné ci-dessous[D 2] pour les premiers hypercubes ; au-delà, l'estimation la plus précise quant au nombre de circuits hamiltoniens dans est donnée[D 3] par :
.

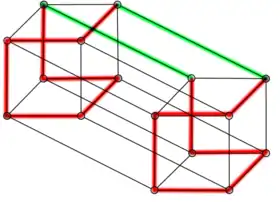
| n | Sans compter les cycles isomorphes | En comptant tous les cycles |
|---|---|---|
| 2 | 1 | 1 |
| 3 | 1 | 6 |
| 4 | 9 | 1344 |
| 5 | 275 065 | 906 545 760 |
- Graphe de Hamming. Un graphe de Hamming est le graphe obtenu par produit cartésien de graphes complets . L'hypercube étant obtenu par produit cartésien de copies de , il découle de la définition que tout hypercube est isomorphe à . Une définition alternative d'un graphe de Hamming montre le rapport direct avec celle utilisée pour introduire l'hypercube : est le graphe dont les sommets sont , l'ensemble des mots de longueur sur un alphabet , où . Deux sommets sont adjacents dans s'ils sont à une distance de Hamming de 1, c'est-à-dire si leurs étiquettes ne diffèrent que d'un symbole.
- Distance-régulier. Un hypercube est un graphe distance-régulier[B 1] et son vecteur d'intersection est .
- Diagramme de Hasse. L'hypercube est isomorphe au diagramme de Hasse d'une algèbre de Boole à n éléments.
- Reconnaissance. Étant donné une liste d'adjacence, on peut savoir en temps et espace linéaire si le graphe qu'elle représente est un hypercube[A 2].
- Code de Gray[C 1]. Les étiquettes ordonnées des sommets dans un cycle hamiltonien sur définissent le code de Gray sur bits. De plus, ce code suit une construction similaire à celle de l'hypercube : les mots de bits sont déterminés en copiant les mots de puis en rajoutant 0 devant l'original, 1 devant la copie, et en inversant les mots de la copie.
- Distance-unité. L'hypercube est un graphe distance-unité : il peut s'obtenir à partir d'une collection de points du plan euclidien en reliant par une arête toutes les paires de points étant à une distance de 1.
Groupe d'automorphisme
Le groupe d'automorphisme de l'hypercube est d'ordre . Il est isomorphe au produit en couronne des groupes symétriques et : [D 4]. Le produit en couronne de A par B étant défini comme le produit semi-direct où est l'ensemble des fonctions de B dans A et où B agit sur par décalage d'indice :
L'hypercube est un graphe arc-transitif : son groupe d'automorphisme agit transitivement sur l'ensemble de ses arcs. Étant donné deux arêtes e1 = u1v1 et e2 = u2v2 de G, il existe deux automorphismes et tels que , , et , , , .
L'hypercube est donc a fortiori symétrique. Le groupe agit donc également transitivement sur l'ensemble de ses sommets et sur l'ensemble de ses arêtes. En d'autres termes, tous les sommets et toutes les arêtes d'un hypercube jouent exactement le même rôle d'un point de vue d'isomorphisme de graphe.
Le graphe hexaédrique () est l'unique graphe cubique symétrique à 8 sommets[D 5]. Le graphe tesseract () est l'unique graphe symétrique régulier de degrés 4 à 16 sommets[A 3].
Graphe de Cayley
L'hypercube est un graphe de Cayley Cay(G, S) avec :
Cela découle d'une propriété plus générale statuant que tous les graphes de Hamming sont des graphes de Cayley[A 4].
Matrice d'adjacence et spectre
La matrice d'adjacence de l'hypercube est définie ci-dessous. Par la définition récursive de l'hypercube, pour passer à la dimension supérieure , on duplique et connecte les sommets d'origine à leur équivalent dans la copie.
| 0 | 1 | |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 0 |
On obtient ainsi la matrice d'adjacence ci-dessous :
| 00 | 01 | 10 | 11 | |
|---|---|---|---|---|
| 00 | 0 | 1 | 1 | 0 |
| 01 | 1 | 0 | 0 | 1 |
| 10 | 1 | 0 | 0 | 1 |
| 11 | 0 | 1 | 1 | 0 |
Au niveau de la matrice, l'opération passant de à se comprend comme suit : les entrées correspondent à la matrice d'origine, et se trouvent dupliquées en . Dans les autres entrées, on connecte chaque sommet à sa copie. Ainsi, la forme générale de la matrice est donnée de la façon suivante[D 6], où représente la matrice identité de dimension :
Pour comprendre l'évolution du spectre de la matrice en fonction de , il faut revenir à la définition comme produit cartésien. Le spectre d'un produit cartésien est , où est le spectre de et le spectre de ; autrement dit, le spectre est la somme de toutes les paires possibles[A 5]. Sachant que le spectre de est , on en déduit que le spectre de est : en effet, elles correspondent aux combinaisons , , . Si l'on passe au stade suivant, soit , on a d'un côté le spectre de , et de l'autre de : le résultat du produit cartésien est .
On en déduit par récurrence la formule suivante pour le polynôme caractéristique de la matrice d'adjacence (et donc du graphe):
- . Ce polynôme caractéristique n'admet que des racines entières. Le graphe d'un hypercube est donc un graphe intégral, un graphe dont le spectre est constitué d'entiers.
Navigation
Pour aller d'un sommet à un autre, on utilise à nouveau le fait que deux sommets sont connectés s'ils diffèrent exactement sur un symbole de leurs étiquettes. Ainsi, un chemin est trouvé en faisant correspondre une à une les coordonnées du sommet de destination avec celui d'origine. Par exemple, pour aller de à , on obtient . Dans le cas général, pour aller de à on obtient :
Notons deux choses. Premièrement, la longueur d'un chemin entre deux sommets est le nombre de symboles sur lesquels leurs étiquettes diffèrent : ainsi, si les étiquettes sont complètement différentes, le chemin sera de longueur , ce qui est une autre explication quant au diamètre du graphe. Deuxièmement, le chemin choisi n'est pas unique : au lieu d'aller de en , on aurait tout d'abord pu passer par avant d'aller en . Le nombre de chemins différents pour aller entre deux sommets est un problème de combinatoire : considérons que les sommets diffèrent sur symboles, combien de façons a-t-on de générer des chemins ? On a choix pour le premier symbole à changer, puis choix pour le second symbole à changer, jusqu'à un seul choix quand il n'y a plus qu'un symbole à changer ; ainsi, le nombre de chemins entre deux sommets différant sur symboles est .
Hypercubes induits
Les chemins entre deux sommets ont d'autres propriétés intéressantes, particulièrement pour les sous-graphes qu'ils définissent. Ainsi, l'union des chemins entre deux sommets distants de (i.e. différant de symboles) donne[A 2] l'hypercube . Ceci est illustré par l'exemple ci-dessous : dans le cas de deux sommets voisins et , il n'y a qu'un chemin et on obtient l'hypercube ; dans le cas où ils sont à distance 2, il y a deux chemins entre eux qui définissent , et s'ils sont à distance 3 alors l'union des chemins représente l'ensemble de l'hypercube .
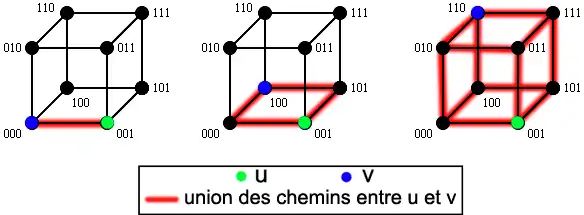
Le nombre d'hypercubes compris dans est donné par la formule suivante[D 7] :
L'hypercube est aussi un graphe médian, et en particulier le seul graphe médian régulier. On peut donc appliquer la formule suivante des graphes médians[D 7] :
Spanners
Certains types de sous-graphe sont particulièrement utiles en termes de communications. Par exemple, un spanner est un sous-graphe couvrant, c'est-à-dire qui contient tous les sommets, mais qui contient moins d'arêtes. Contenir moins d'arêtes peut augmenter les distances entre des sommets du graphe, et l'on distingue ainsi les spanners multiplicatifs, où la distance peut être multipliée par un facteur , des spanners additifs où la distance peut être augmentée d'un montant . Dans le cas d'un spanneur additif sur , des résultats[D 8] concernent les degrés du spanneur :
- si et , alors le plus petit degré maximal est .
- si et est grand, il existe un spanneur de degré moyen au plus .
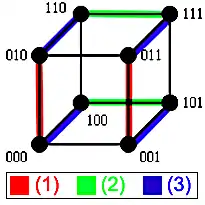
De nombreuses études sur les spanners, et des constructions pour des modèles généralisés de l'hypercube, sont dues à Arthur L. Liestman et Thomas C. Shermer[B 2]. Ils ont en particulier proposé un spanner additif avec un montant où les arêtes sont celles dont les extrémités sont données par les trois conditions suivantes :
Ce processus est illustré dans l'image ci-contre où les arêtes satisfaisant une des conditions sont surlignées ; l'ensemble de ces arêtes constitue le spanner. Pour obtenir un chemin entre deux sommets, considérons que l'on démarre d'un sommet . On inverse d'abord ses coordonnées paires, car la condition (1) impose l'existence d'une arête sur tout sommet commençant par 0 avec une différence sur bit pair. On change ensuite la première coordonnée en 1 grâce à la condition (3), à partir de quoi on peut inverser toutes les coordonnées impaires par la condition (2). Si le sommet de destination est alors on est arrivé car on commence par 1 et les coordonnées paires comme impaires ont pu être inversé ; si le sommet de destination est on utilise une dernière inversion par la condition (3). Le cas où le sommet d'origine est est traité de façon similaire : inverser les coordonnées impaires, passer la première coordonnée en 0, inverser les coordonnées paires, passer la première coordonnée en 1 si nécessaire. Dans l'image ci-contre, on voit le délai de 2 si on cherche un chemin de à : ce qui se ferait normalement directement en une étape doit se faire en trois étapes, en passant par et .
Diffusions
Dans le problème de la diffusion (anglais broadcast), un nœud source souhaite diffuser une information à tous les autres nœuds. Dans le modèle classique, à chaque étape un nœud donné peut transmettre au plus une information, cette information utilisant une arête et étant transmise à la fin de l'étape. Dans ce modèle, la diffusion la plus performante est celle où, à chaque étape, chaque nœud en contacte un autre, c'est-à-dire que le nombre de nœuds contactés est doublé. Le nombre d'étapes minimal est donc ; un graphe pouvant finir une diffusion en étapes quelle que soit l'origine et en minimisant le nombre d'arêtes est un graphe de diffusion minimale (anglais minimal broadcast graph). Dans le cas où , le nœud source doit avoir au moins voisins car il doit diffuser à chaque étape pour faire doubler le nombre de voisins ; la source n'étant pas fixée, on obtient que chaque nœud doit avoir au moins voisins d'où arêtes ( vient du partage de chaque arête dans un graphe non-orienté), ce qui est précisément le cas d'un hypercube. Ainsi, l'hypercube est un graphe de diffusion minimale.
Parmi les problèmes proches se trouve le commérage (anglais gossip) où chaque nœud veut échanger une information avec tous les autres, autrement dit chaque nœud est la source d'une diffusion. Des cas particuliers s'intéressent aux variantes locales : par exemple, dans un commérage 'local', chaque nœud veut apprendre les messages de ses voisins[D 9].
Utilisations
Architectures de machines parallèles
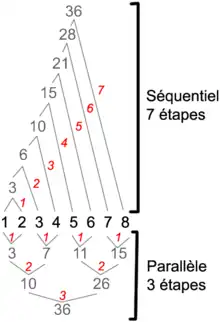
Pour avoir une idée du gain en performances en utilisant des machines parallèles, considérons l'addition de nombres. Sur une machine séquentielle, on additionne le premier nombre avec le second, puis on rajoute le troisième, etc., Au total, étapes sont nécessaires. Sur une machine parallèle, chaque processeur réalise l'addition d'une paire de nombres en une étape, puis les résultats de deux paires sont additionnés, etc. Au total, étapes sont nécessaires. Ainsi, pour 1 000 nombres, une machine séquentielle utilisera 999 étapes tandis qu'il n'en faut que 11 sur une machine parallèle ; un autre exemple est illustré ci-contre. Le gain est encore plus significatif pour d'autres opérations, par exemple une instance d'inversion de matrice peut nécessiter 40 000 étapes sur une machine séquentielle contre 61 sur une machine parallèle[A 6].
Au début des années 1960, des idées furent proposées pour concevoir un ordinateur parallèle avec une architecture en hypercube : « il y a modules, chacun connecté directement à autres ; en particulier, chaque module est placé sur le sommet d'un cube n-dimension, et les arêtes de ce cubes sont les câbles »[A 6]. Les justifications dans le choix de l'hypercube peuvent paraître faibles au regard des connaissances actuelles sur les familles de graphes, mais il s'avère que l'hypercube a de nombreuses propriétés utiles : il est arc-transitif et distance-transitif, ce qui implique que toutes ses arêtes jouent le même rôle et que tous ses sommets ont les mêmes propriétés de distance. Par ailleurs, le compromis entre le degré des sommets et la distance entre eux reste raisonnable, et la navigation peut se faire de façon délocalisée, ce qui est une des principales raisons citées à l'origine. En résumé, les propriétés de transitivité permettent d'obtenir une égalité entre les processeurs, et la communication entre les processeurs peut être rapide (distance faible) en ayant besoin de peu d'informations (délocalisé).
Vingt ans se sont écoulés entre les idées du début des années 1960 et la première production, avec le Cosmic Cube[D 10] de Caltech (64 processeurs Intel 8086/86 embarquant chacun 128Kb de mémoire) en 1983. De nombreuses autres machines sont alors produites, comme les Ametek série 2010, les Connection Machine (en)[D 11] CM-1/CM-2, les nCUBE (en) et les iPSC d'Intel. De nombreuses études sur les performances des machines parallèles utilisant une architecture en hypercube sont réalisées au laboratoire national d'Oak Ridge sous le contrat DE-AC05-84OR21400[D 12]. En effet, ce laboratoire créé à l'origine pour le Projet Manhattan (conception de la première bombe atomique) s'est reconverti sur des sujets tels que la sécurité nationale et les supercalculateurs. Parmi les modèles étudiés figurent les Intel iPSC/860, iPSC/1 et iPSC/2, ainsi que les nCUBE 3200 et 6400 ; les caractéristiques de ces machines sont résumées ci-dessous.
| iPSC/860 | iPSC/2 | iPSC/1 | N6400 | N3200 | |
|---|---|---|---|---|---|
| Nombre de nœuds | 128 | 64 (max 128) | 64 (max 128) | 64 (max 8192) | 64 (max 1024) |
| Processeur du nœud | Intel i860 | Intel 80286/387 | Intel 80386/287 | 64-bit | 32-bit |
| Fréquence d'horloge | 40 MHz | 16 MHz | 8 MHz | 20 MHz | 8 MHz |
| Mémoire par nœud | 8M | 4M (max 16M) | 512K (max 4.5M) | 4M (max 64M) | 512K |
| Débit nominal | 22 Mb/s | 22 Mb/s | 10 Mb/s | 20 Mb/s | 8 Mb/s |
| Système d'exploitation | NX V3.2 | XENIX | XENIX | Vertex v2.0 | Vertex 2.3 |
Les performances précises de ces processeurs peuvent être trouvées dans les rapports d'Oak Ridge. Au niveau de l'analyse des performances pour la communication, il est préférable d'utiliser un modèle à coût linéaire plutôt qu'à coût constant. Autrement dit, on ne peut pas considérer qu'envoyer un message ait un coût en temps fixe quelle que soit la longueur du message : on considère plutôt que le coût en temps est fonction de la longueur du message, et qu'initier la transmission a également un coût , ce qui entraîne le modèle . Le coût est significatif par rapport à : cela prend par exemple prend 697µs pour établir la communication dans un iPSC/2, mais seulement 0.4µs pour chaque bit transmit.
Répartir les données sur un hypercube


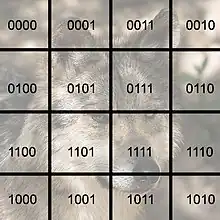

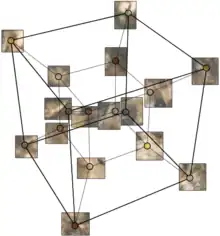
De nombreuses informations sur les algorithmes pour des architectures en hypercubes à la fin des années 80 furent publiées dans la troisième conférence Hypercube Concurrent Computers and Applications[A 7] (« Ordinateurs concurrents en hypercube et applications »). Utiliser une machine parallèle n'augmente pas automatiquement la performance d'un algorithme : non seulement les algorithmes doivent être conçus de façon à tirer profit de l'architecture, mais les données ne peuvent pas toujours être partitionnées pour être traitées par différents processeurs, et ces processeurs ont également besoin de communiquer. Dans l'exemple de l'addition, le coût de communication était considéré comme négligeable, et ceci est l'hypothèse que nous conserverons par la suite : en effet, les propriétés de la machine (temps de communication, lecture/écriture, ...) sont généralement ignorés dans l'analyse des algorithmes, et on se concentre sur les dépendances entre les données et les façons de rendre le calcul parallèle sur un hypercube.
Une des opérations les plus courantes en traitement d'image consiste à utiliser un filtre linéaire, c'est-à-dire à appliquer une matrice de convolution. Pour bénéficier de l'architecture en hypercube, l'image doit être divisée en zones égales, et chaque zone assignée à un processeur. Mudge et Abdel-Rahman ont suggéré de considérer l'image comme étant une table de Karnaugh utilisant le code de Gray[D 13], ainsi que sur l'exemple ci-contre : si on considère une zone de l'image et ses coordonnées dans la table, alors on obtient directement le processeur auquel l'assigner. Par ailleurs, l'utilisation du code de Gray conserve l'adjacence : deux zones adjacentes dans l'image seront placées sur deux processeurs adjacents, sauf pour les coins. Le filtre, tel que celui de Sobel, est appliqué par chaque processeur à la zone qui lui est assignée. Si le filtre a besoin de certains pixels dépassant la zone disponible à un processeur, il peut la demander au processeur voisin en utilisant les propriétés d'adjacence ; pour des coûts plus faibles en communication, chaque processeur peut également avoir une zone de l'image dont la taille correspond à celle nécessaire pour le traitement plutôt qu'à une partition stricte.
Réutilisation d'algorithmes par plongements
Un plongement permet à ce qu'un réseau soit simulé par un autre : aux sommets du réseau d'origine sont associés des sommets dans le réseau simulant, et deux sommets voisins sont séparés par un chemin. Ainsi, un algorithme conçu spécialement pour un réseau peut être réutilisé dans un autre grâce à un plongement. On s'intéresse donc à deux cas : réutiliser des algorithmes sur des hypercubes (1), ou utiliser des algorithmes pour l'hypercube dans d'autres réseaux (2). Autrement dit, l'hypercube est soit un réseau simulant (1), soit un réseau simulé (2). La qualité d'un plongement permet de savoir quelles sont les différentes pertes en performance de l'algorithme. Pour cela, on considère plusieurs facteurs[C 2] :
- Congestion. Elle donne le ralentissement si plusieurs arêtes du réseau simulé sont utilisées simultanément : elle mesure le nombre d'arêtes du réseau simulé qui sont associées à une seule arête dans le réseau simulant, et ainsi une congestion de 2 indique que le réseau simulant aura besoin de 2 étapes pour transporter les messages que le réseau simulé pouvait avoir en une étape.
- Dilatation. Elle peut être considérée comme le ralentissement des communications : elle mesure l'augmentation de la distance entre deux sommets dans le réseau simulant par rapport au simulé, et ainsi une dilatation de 2 signifie que toute communication qui se faisait en une étape en prendra maintenant 2.
- Charge. Elle indique le ralentissement pour le calcul sur un processeur : elle donne le nombre de sommets du réseau simulé associés à un seul sommet dans le réseau simulant
Pour l'hypercube comme réseau simulant, toute grille à deux dimensions a un plongement[C 1] avec une dilatation d'au plus 2 et une expansion minimale, une grille à trois dimensions a une dilatation entre 2 et 5, et l'arbre binaire complet à nœuds a un plongement de dilatation 1 sur .
Parallélisme automatique
Si un programme utilise plusieurs tâches et que l'on a des informations sur la façon dont ces tâches communiquent, alors il peut être possible de faire bénéficier le programme d'une machine parallèle. En effet, la structure de la communication des tâches définit un graphe, et celui-ci peut être simulé entre autres par un hypercube en cherchant un plongement, tel qu'étudié dans la section précédente. Dans l'autre cas extrême, si toute tâche communique fréquemment avec toutes les autres, alors les communications sont données par un graphe complet et la simulation par une machine parallèle est peu performante. Des solutions intermédiaires ont été développées s'il n'y a pas d'informations sur la communication des tâches mais qu'elle se fait à fréquence modérée[D 14].
Variantes
L'hypercube était très utilisé pour les architectures de machines parallèles, et certaines de ses propriétés étaient jugées perfectibles dans ce cadre. Le principal problème est la croissance d'un hypercube, où le nombre de sommets doit doubler d'une dimension à l'autre : dans une machine, plus de flexibilité est désirable afin de pouvoir ajouter quelques processeurs. Plusieurs aspects sont aussi liés à sa réalisation par des circuits électroniques. Premièrement, l'hypercube n'est pas planaire et aura donc des chevauchements dans le circuit : en réduire le nombre simplifie le circuit. Deuxièmement, l'hypercube est défini comme un graphe non-orienté, mais « un réseau basé sur une orientation de utilise la moitié du nombre de broches et câbles par rapport à »[D 15] : il est donc intéressant de trouver une orientation conservant des performances similaires. Enfin, il peut être désirable de réduire les distances dans l'hypercube pour les performances en termes de communications.
L'hypercube comme bloc de base
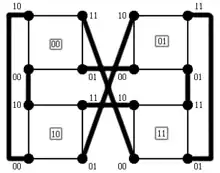
Un hierarchical cubic network[D 16] est formé de -cubes, où chaque cube est désigné comme un cluster. Chacun de ces clusters est utilisé comme un bloc de base, et chaque nœud d'un cluster a un lien supplémentaire le reliant à un autre cluster ; ces liens sont déterminés par l'algorithme suivante pour le graphe composé de -cubes, où désigne le sommet du cluster et est le complément bit à bit de :
Les auteurs montrèrent que, à tailles égales, ce graphe a un diamètre d'un quart plus faible que celui de l'hypercube, et la moitié du nombre de liens. Cependant, dans certaines situations la diffusion est plus lente que sur un hypercube, et avoir un graphe moins dense revient à être plus exposé lorsque des pannes surviennent sur les liens.
Cubes de Fibonacci
Une autre variante ayant été depuis particulièrement étudiée est le Cube de Fibonacci[D 17]. Les conditions fondamentales du cube de Fibonacci de dimension , noté , sont les mêmes que celles de l'hypercube : chaque sommet porte une étiquette de longueur sur un alphabet , et deux sommets sont adjacents si leurs étiquettes ne différent que d'un symbole. Cependant, on rajoute une contrainte : une étiquette valide ne peut avoir deux consécutif. Ainsi, ci-dessous, on voit que les cubes de Fibonacci peuvent se retrouver comme sous-graphes des hypercubes en éliminant les étiquettes contenant deux consécutifs.
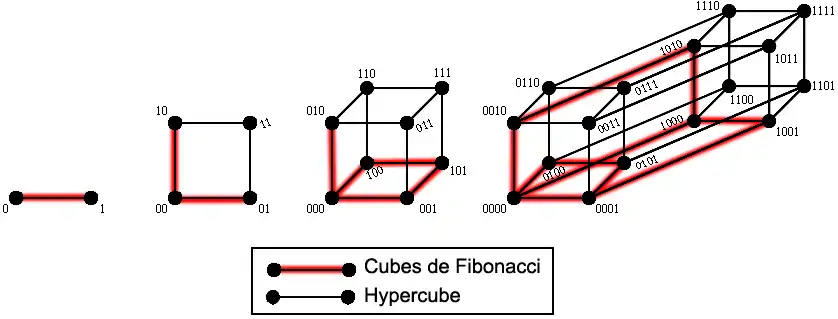
La construction par récurrence [D 18] peut être définie par une grammaire formelle en énonçant les étiquettes valides pour les sommets, puis en considérant le graphe comme le sous-graphe de l'hypercube induit par les sommets valides :
Hypercubes recâblés
Dans le cas où réduire la distance soit le principal objectif, il est courant d'utiliser des procédures de recâblage comme on le voit encore dans le cas de l'effet petit monde. De nombreuses procédures ont été proposées, et les plus significatives sont résumées dans le tableau ci-dessous avec leurs performances sur la distance maximale (i.e. le diamètre) et moyenne ainsi que le nombre de recâblages nécessaire. Le nom de chacune des procédures est conservé à partir des articles d'origines, où twisted signifie recâblé, et suivi de l'année à laquelle la procédure fut publiée.
| Nom | Diamètre | Distance moyenne | Nombre d'arêtes recâblées |
|---|---|---|---|
| Hypercube | 0 | ||
| Twisted cube (1987) | |||
| Twisted hypercube (1991) | |||
| Twisted N-cube (1991) | |||
| Generalized twisted cube (1993) | |||
| 0-Möbius Cube (1995) |
Graphe libre d'échelle par contraction
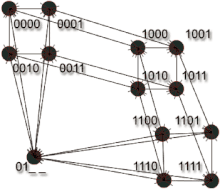
Dans les années 2000, de nombreux modèles furent proposés pour prendre en compte des caractéristiques communes à de nombreux réseaux. Deux des principales caractéristiques sont l'effet petit monde et l'effet libre d'échelle. Il est possible de modifier un hypercube afin d'obtenir l'effet libre d'échelle, tout en continuant à bénéficier de sa propriété de routage local[C 3]. Pour cela, des sommets sont contractés à la condition qu'ils ne diffèrent que sur une coordonnée qui sera remplacé par un joker « _ ». Après une séquence de contractions, c'est-à-dire plusieurs contractions successives, il est toujours possible de trouver un chemin d'un sommet à un sommet en utilisant leurs coordonnés et en remplaçant les jokers « _ » par les coordonnées de .
La condition de ne différer que sur une coordonnée tout en opérant une séquence de contractions conduit à ce qu'un sous-hypercube soit contracté, et le degré du sommet résultant de la contraction d'un hypercube dans , est :
En résumé, l'effet libre d'échelle est obtenu par contraction de sous-hypercubes de grande taille et les algorithmes de navigation n'ont pas besoin d'être modifiés.
Galerie
Références
|
|
Voir aussi
Bibliographie
- (en) Frank Harary, John P. Hayes et Horng-Jyh Wu, « A survey on the theory of hypercube graphs », Computers & Mathematics with Applications, vol. 15, no 4, , p. 277-289 (DOI 10.1016/0898-1221(88)90213-1, lire en ligne).