Graphe cubique

Une conséquence du lemme des poignées de main est que tout graphe cubique a un nombre pair de sommets.

D'après le théorème de Brooks, les sommets d'un graphe cubique peuvent être coloriés avec trois couleurs (ou moins) de telle sorte que deux sommets adjacents ne soient pas de la même couleur, sauf dans le cas du graphe tétraédrique ${\displaystyle K_{4}}$.

Un graphe bicubique est un graphe biparti régulier de degré 3, c'est-à-dire un graphe cubique dont les sommets peuvent être coloriés avec deux couleurs seulement.

• 
  Le graphe complet ${\displaystyle K_{4}}$ est le seul graphe cubique nécessitant 4 couleurs
• 
  Coloration du graphe de Frucht avec 3 couleurs
• 
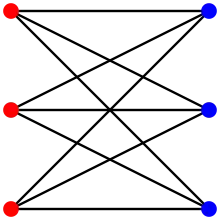  ${\displaystyle K_{3,3}}$ est un graphe bicubique, 2 couleurs suffisent
• 
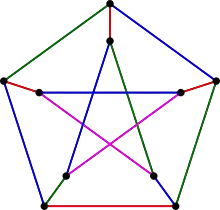  Les arêtes du graphe de Petersen, un snark, ont besoin de 4 couleurs

D'après le théorème de Vizing, les arêtes d'un graphe cubique peuvent être colorées avec 3 ou 4 couleurs sans que deux arêtes de même couleur ne soient incidentes au même sommet. Les snarks sont les graphes cubiques connexes et sans isthme qui ont besoin de 4 couleurs.

Le théorème de Petersen précise que tout graphe cubique sans isthme possède un couplage parfait[1].

En d'autres termes, si, dans un graphe cubique, toute arête appartient à un cycle, alors il existe un ensemble d'arêtes qui sont incidentes à tous les sommets, chaque sommet n'étant l'extrémité que d'une seule de ces arêtes.

Ce théorème, un des plus anciens de la théorie des graphes, puisqu'il date de 1891, est vu de nos jours comme une application du théorème de Tutte (en).

• 
  Un exemple de couplage parfait dans un graphe non cubique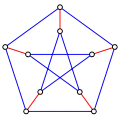
• 
  Les arêtes rouges forment un couplage parfait du graphe de Petersen.

Le théorème a été généralisé : une conjecture, formulée par Michael D. Plummer et László Lovász dit que tout graphe cubique sans isthme possède un nombre exponentiel de couplages parfaits. Cette conjecture a été démontrée par Esperet, Kardoš, King et Kráľ en 2011[2].

Dans un graphe hamiltonien, on peut passer par tous les sommets une fois et une seule.

La plupart des graphes cubiques sont hamiltoniens, mais pas tous : la probabilité d'être hamiltonien tend vers 1 quand le nombre de sommets augmente indéfiniment[3].

Les graphes cubiques peuvent même être à la fois polyédriques, cubiques et non hamiltoniens, comme le montre le graphe de Tutte. Ils peuvent aussi être à la fois bicubiques et non hamiltoniens, comme le montrent le graphe de Horton ou le 54-graphe de Ellingham-Horton. La conjecture de Barnette, encore non prouvée et non infirmée pour le moment, affirme que tout graphe à la fois bicubique et polyédrique serait hamiltonien.

Quand un graphe cubique est hamiltonien, la notation LCF permet de le représenter de façon concise.

• 
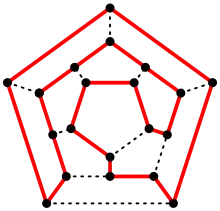  Un cycle hamiltonien dans le graphe dodécaédrique
• 
  Le cube de Bidiakis, représenté de façon à mettre en évidence qu'il est polyédrique
• 
  Le cube de Bidiakis, arrangé autrement : le cercle met en évidence un cycle hamiltonien