Notation LCF

Le graphe de Foster a pour notation LCF [17, −9, 37, −37, 9, −17]¹⁵.

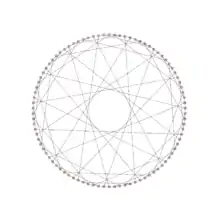
Comme le graphe est hamiltonien, les sommets peuvent être arrangés en cercle, chaque sommet ayant deux arêtes sur le cercle. La troisième arête peut être décrite par le nombre de positions sur le cercle qu'il faut parcourir pour atteindre l'autre extrémité de l'arête. Si l'on parcourt ces positions dans le sens des aiguilles d'une montre, on considère le nombre comme positif, et si on les parcourt dans le sens inverse des aiguilles d'une montre, on le considère comme négatif.

Comme cette suite de nombres se répète souvent, on abrège la notation en notant le nombre de répétitions du motif de base en exposant. Par exemple, le graphe de Nauru[2] (figure) a pour notation LCF [5, −9, 7, −7, 9, −5]⁴.

Le même graphe peut être représenté par plusieurs notations LCF différentes, selon la façon dont les sommets sont arrangés.

Les nombres entre crochets sont pris entre 2 et N−2, N étant le nombre de sommets. Les nombres 0, 1 et N−1 ne sont pas permis, puisque les arêtes correspondantes mèneraient soit au sommet lui-même, soit à ses voisins sur le cycle[3].

La notation LCF fournit une description concise des graphes cubiques hamiltoniens, utile dans les publications papier.

En outre, des logiciels de manipulation de graphes comprennent des utilitaires pour créer un graphe à partir de sa notation LCF. On peut citer Maple, NetworkX, R et sage.