Graphe asymétrique

En théorie des graphes, un graphe asymétrique ou graphe identité est un graphe dont le groupe d'automorphismes est trivial. C'est donc un graphe n'admettant aucun automorphisme autre que l'identité.

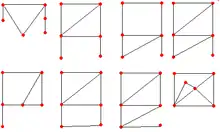
Le plus petit graphe asymétrique est le graphe singleton, qui est également un graphe symétrique. Si on exclut ce cas trivial, un graphe asymétrique doit avoir au moins 6 sommets[1]. Il existe 8 graphes asymétriques distincts à isomorphisme près à l'ordre 6, 152 à l'ordre 7, 3 696 à l'ordre 8, 135 004 à l'ordre 9, 7 971 848 à l'ordre 10 et 805 364 776 à l'ordre 11[2].

Parmi les graphes cubiques, le plus petit graphe asymétrique est le graphe de Frucht. Il a 12 sommets.

Sont également asymétriques le graphe de Kittell, le graphe 4-chromatique de Heawood et le graphe de Walther.

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.