Graphe fortement régulier
En théorie des graphes, qui est un domaine des mathématiques, un graphe fortement régulier est un type de graphe régulier.
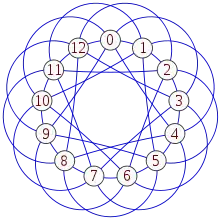
Le graphe de Paley d'ordre 13, un graphe fortement régulier de type (13,6,2,3).
Définition
Soit G = (V,E) un graphe régulier ayant v sommets et degré k. On dit que G est fortement régulier[1] s'il existe deux entiers λ et μ tels que
- Toute paire de sommets adjacents a exactement λ voisins communs.
- Toute paire de sommets non-adjacents a exactement μ voisins communs.
Un graphe avec ces propriétés est appelé un graphe fortement régulier de type (v,k,λ,μ).
Lorsque μ n'est pas nul, un tel graphe est en particulier un graphe distance-régulier.
Propriétés
| Familles de graphes définies par leurs automorphismes | ||||
|---|---|---|---|---|
| distance-transitif | → | distance-régulier | ← | fortement régulier |
| ↓ | ||||
| symétrique (arc-transitif) | ← | t-transitif, (t ≥ 2) | symétrique gauche (en) | |
| ↓ | ||||
| (si connexe) sommet-transitif et arête-transitif |
→ | régulier et arête-transitif | → | arête-transitif |
| ↓ | ↓ | ↓ | ||
| sommet-transitif | → | régulier | → | (si biparti) birégulier |
| ↑ | ||||
| graphe de Cayley | ← | zéro-symétrique | asymétrique | |
- Les quatre paramètres (v,k,λ,μ) vérifient toujours la relation suivante :
- Un graphe fortement régulier de type (v,k,λ,μ) a exactement trois valeurs propres distinctes :
- avec multiplicité 1
- avec multiplicité
- avec multiplicité
- Les graphes fortement réguliers dont les paramètres vérifient sont nommés graphes de conférence à cause de leur relation avec les matrices de conférence. Leur type est .
- Le graphe complémentaire d'un graphe fortement régulier de type (v,k,λ,μ) est aussi fortement régulier, de type (v, v−k−1, v−2−2k+μ, v−2k+λ).
Exemples
- Le graphe de Shrikhande de type (16,6,2,2).
- Le cycle de longueur 5, de type (5,2,0,1).
- Le graphe de Petersen de type (10,3,0,1).
- Les graphes de Chang de type (28,12,6,4).
- Le graphe de Hoffman-Singleton de type (50,7,0,1).
- Le graphe de Higman-Sims de type (100,22,0,6).
- Le graphe de Paley d'ordre q dont le type est (q, (q − 1)/2, (q − 5)/4, (q − 1)/4.
- Le graphe de Brouwer-Haemers de type (81,20,1,6).
- Le graphe de Schläfli de type (27,16,10,8).
- Le graphe local de McLaughlin de type (162,56,10,24).
Notes et références
Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.


![{\frac {1}{2}}\left[(\lambda -\mu )+{\sqrt {(\lambda -\mu )^{2}+4(k-\mu )}}\right]](https://img.franco.wiki/i/28d663f8d1414600891d64ce50684f5957386e52.svg)
![{\frac {1}{2}}\left[(v-1)-{\frac {2k+(v-1)(\lambda -\mu )}{{\sqrt {(\lambda -\mu )^{2}+4(k-\mu )}}}}\right]](https://img.franco.wiki/i/bbc8e9b9ead0ab886e5b0a9b462a154538d4f273.svg)
![{\frac {1}{2}}\left[(\lambda -\mu )-{\sqrt {(\lambda -\mu )^{2}+4(k-\mu )}}\right]](https://img.franco.wiki/i/ab7d1d14bcb237dd04960ff149494b1d3ca60f2a.svg)
![{\frac {1}{2}}\left[(v-1)+{\frac {2k+(v-1)(\lambda -\mu )}{{\sqrt {(\lambda -\mu )^{2}+4(k-\mu )}}}}\right]](https://img.franco.wiki/i/10c4e7c6833df4ca6e1613efb30a7f10d594d563.svg)

