Matrice de conférence

En mathématiques, une matrice de conférence (également appelé C-matrice) est une matrice carré $C$ qui a des 0 sur la diagonale et des +1 et -1 en dehors de la diagonale, de telle sorte que la matrice $C^{t}C$ est un multiple de la matrice identité $I$ [1].

Définition

Si une matrice de conférence est d'ordre n, alors $C^{t}C=(n-1)I$ . Une définition plus générale demande qu'il y ait un 0 unique dans chaque ligne et colonne mais pas nécessairement sur la diagonale[2] - [3]

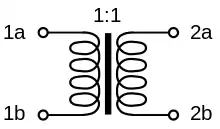
Le réseau de conférence trivial à 2 ports.

Les matrices de conférence sont d'abord apparues en rapport avec un problème de téléphonie[4]. Ils ont été décrits pour la première fois par Vitold Belevitch, qui leur a également donné leur nom. Belevitch était intéressé par la construction de réseaux de conférence téléphonique à partir de transformateurs idéalisés et il a découvert que ces réseaux étaient représentés par des matrices de conférence, ce qui leur a valu ce nom[5]. D'autres applications existent en statistique[6] et une autre en géométrie elliptique[7].

Propriétés

Une matrice de conférence est d'ordre pair[8]. Plus précisément, on a le résultat suivant :

Théorème — S'il existe une matrice de conférence d'ordre $n$ pour un entier $n$ , alors $n$ est pair ; de plus, si $n\equiv 2({\bmod {4}})$ , alors, pour tout nombre premier $p\equiv 3({\bmod {4}})$ , la plus haute puissance de $p$ divisant $n-1$ est paire[9].

Pour $n>1$ , une normalisation conduit à deux types de matrices de conférence, les unes symétriques, les autres antisymétiques. On normalise une matrice $C$ d'abord en réorganisant les lignes pour que tous les zéros soient sur la diagonale, puis on remplace une ligne ou colonne dont la première entrée est négative par son opposée ; ces opérations ne changent pas la nature d'une matrice de conférence. Ainsi, une matrice de conférence normalisée n'a que des 1 dans sa première ligne et sa première colonne, à l'exception d'un 0 dans le coin supérieur gauche, et des 0 sur la diagonale. Soit $S$ la matrice après suppression de la première ligne et de la première colonne de $C$ ; cette matrice est parfois appelée le noyau de $C$ [8]. Alors soit n est un multiple de 4 et $S$ est antisymétrique, soit n est congru à 2 modulo 4 et $S$ est symétrique.

Matrices de conférence symétriques

Définition

Si $C$ est une matrice de conférence symétrique d'ordre n>1, alors non seulement n doit être congru à 2 (mod 4) mais aussi n − 1 doit être une somme de deux carrés[10] ; une preuve élégante de cette propriété au moyen de la théorie des matrices élémentaires est donnée par van Lint et Seidel[7]. L'entier n est toujours la somme de deux carrés si n − 1 est un nombre primaire[11].

Étant donné une matrice de conférence symétrique, la matrice noyau S peut être considérée comme la matrice d'adjacence de Seidel (en) d'un graphe. Le graphe a n − 1 sommets, correspondant aux lignes et colonnes de S, et deux sommets sont adjacents si l'entrée correspondante dans S est négative. Ce graphe est fortement régulier et est appelé, d'après sa matrice, un graphe de conférence.

L'existence de matrices de conférence d'ordre n avec les restrictions ci-dessus n'est connue que pour certaines valeurs de n . Par exemple, si n = q + 1 où q est un nombre primaire congru à 1 (mod 4), alors les graphes de Paley fournissent des exemples de matrices symétriques de conférence d'ordre n, en prenant pour S la matrice de Seidel du graphe de Paley. Les premiers ordres possibles d'une matrice de conférence symétrique sont n = 2, 6, 10, 14, 18, (mais pas 22, puisque 21 n'est pas une somme de deux carrés), 26, 30, (et pas 34 puisque 33 n'est pas un somme de deux carrés), 38, 42, 46, 50, 54, (pas 58), 62. C'est la suite A000952 de l'OEIS ; pour chacun d'entre eux, on sait qu'il existe une matrice de conférence symétrique de cet ordre. L'ordre 66 semble être un problème ouvert.

Exemples

Trois exemples ; on écrit « — » pour « -1 » :

A={\begin{pmatrix}0&1\\1&0\end{pmatrix}}\quad B={\begin{pmatrix}0&1&1&1\\-&0&1&-\\-&-&0&1\\-&1&-&0\end{pmatrix}}\quad C={\begin{pmatrix}0&1&1&1&1&1\\1&0&1&-&-&1\\1&1&0&1&-&-\\1&-&1&0&1&-\\1&-&-&1&0&1\\1&1&-&-&1&0\end{pmatrix}}

La matrice de conférence C d'ordre 6 est essentiellement unique, au sens que les autres matrices de conférence d'ordre 6 sont obtenues à partir de celle-ci en inversant les signes d'une ligne et / ou d'une colonne (et en effectuant des permutations de lignes et / ou de colonnes, selon la définition utilisée).

Matrices de conférence antisymétriques

Des matrices antisymétriques peuvent également être produites par la construction de Paley. Soit q un nombre primaire congru à 3 (mod 4). Alors il existe un graphe de Paley orienté d'ordre q qui donne une matrice de conférence antisymétrique d'ordre n = q + 1. La matrice est obtenue en prenant pour S la matrice d'ordre q × q qui a un +1 en position (i, j ) et −1 en position ( j, i ) s'il y a un arc du graphe de i à j, et 0 sur la diagonal. La matrice C construite comme ci-dessus à partir de S, mais avec la première ligne entièrement négative, est une matrice de conférence antisymétrique.

Cette construction ne répond que partiellement au problème de déterminer les nombres n pour lesquels il existe une matrices de conférence antisymétriques d'ordre n .

Généralisations

Parfois, une matrice de conférence d'ordre n est simplement définie comme une matrice pondérée particulière : on appelle dans ce contexte une matrice de poids w>0 et on note $W(n,w)$ une matrice carrée de taille n avec des entrées dans {−1, 0, +1} satisfaisant $WW^{t}=wI$ [3]. En utilisant cette définition, l'entier zéro n'est plus forcément sur la diagonale, mais il est facile de voir qu'il doit encore y avoir exactement un zéro dans chaque ligne et colonne. Par exemple, la matrice

{\begin{pmatrix}1&0&1&1\\0&-&-&1\\1&-&0&-\\1&1&-&0\end{pmatrix}}

satisfait cette définition moins forte, mais pas la définition plus stricte qui demande que les éléments nuls soient sur la diagonale.

Un design de conférence est une autre généralisation des matrices de conférence, aux matrices non carrés. Un design de conférence $C$ est une matrice $N\times k$ , avec des entrées dans {-1, 0, +1} satisfaisantes $W^{t}W=(N-1)I_{k}$ , où $I_{k}$ est le $k\times k$ matrice d'identité, et avec au plus un zéro dans chaque ligne. Les design « repliables » des design de conférence peuvent être utilisées comme design de projection[12] - [13].

Circuits de conférence téléphonique

Réseau de conférence à 6 ports.

Réseau de conférence à 10 ports.

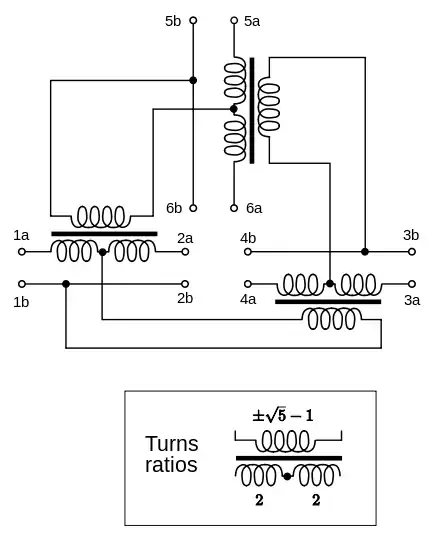
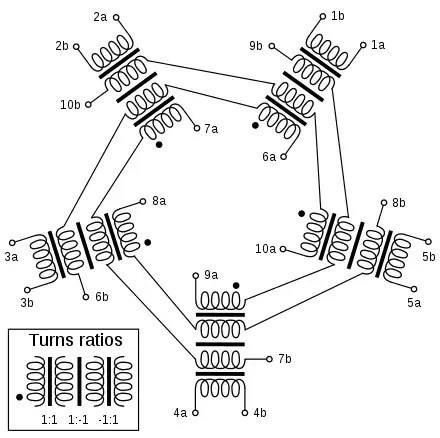
Belevitch a obtenu des solutions complètes pour les matrices de conférence pour toutes les valeurs de n jusqu'à 38 et a fourni des circuits pour certaines des plus petites matrices. Un réseau de conférence idéal est un réseau dans lequel la perte de signal est entièrement due au fait que le signal est divisé entre plusieurs ports d'abonnés à la conférence. Autrement dit, il n'y a pas de pertes par dissipation dans le réseau. Le réseau contient uniquement des transformateurs idéaux et aucune résistance. Un réseau de conférence idéal à n ports existe si et seulement s'il existe une matrice de conférence d'ordre n . Par exemple, un réseau de conférence à 3 ports peut être construit avec le circuit de transformateur hybride bien connu utilisé pour la conversion de 2 fils en 4 fils dans les combinés téléphoniques et les répéteurs de ligne. Cependant, il n'y a pas de matrice de conférence d'ordre 3 et ce circuit ne produit pas un réseau de conférence idéal. Une résistance est nécessaire pour l'adaptation qui dissipe le signal, sinon le signal est perdu en raison d'une discordance[14].

Comme mentionné ci-dessus, une condition nécessaire pour qu'une matrice de conférence existe est que n − 1 est la somme de deux carrés. Lorsqu'il y a plus d'une expression comme de deux carré pour n − 1, il existe plusieurs solutions essentiellement différentes pour le réseau de conférence correspondant. Cette situation se produit pour n égal à 26 ou 66. Les réseaux sont particulièrement simples lorsque n − 1 est un carré parfait ( n = 2, 10, 26,…)[15].

Notes

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Conference matrix » (voir la liste des auteurs).

$C^{t}$ est la matrice transposée de $C$
Greig Malcolm, « On the coexistence of conference matrices and near resolvable 2-(2k+1,k,k-1) designs », Journal of Combinatorial Theory, Series A, vol. 113, n^o 4,‎ 2006, p. 703–711 (DOI 10.1016/j.jcta.2005.05.005)
Gropp Harald, « More on orbital matrices », Electronic Notes in Discrete Mathematics, vol. 17,‎ 2004, p. 179–183 (DOI 10.1016/j.endm.2004.03.036)
Belevitch, p. 231-244.
Colbourn and Dinitz, (2007), p. 19, van Lint and Wilson, (2001), p. 98, Stinson, (2004), p. 200.
D. Raghavarao, « Some optimum weighing designs », Annals of Mathematical Statistics, vol. 30, n^o 2,‎ 1959, p. 295–303 (DOI 10.1214/aoms/1177706253, MR 0104322).
J. H. van Lint et J. J. Seidel, « Equilateral point sets in elliptic geometry », Indagationes Mathematicae, vol. 28,‎ 1966, p. 335–348.
Ionin Kharachani, p. 306-309.
Ionin Kharachani, Theorem 6.3.
Belevitch, p. 240
Stinson, p. 78.
Xiao et al. (2012)
Schoen et al. (2018).
Belevitch, p. 240-242.
Belevitch, p. 242.

Références

Vitold Belevitch, « Theory of 2n-terminal networks with applications to conference telephony », Electrical Communication, vol. 27,‎ 1950, p. 231–244
J. M. Goethals et J. J. Seidel, « Orthogonal matrices with zero diagonal », Canadian Journal of Mathematics, vol. 19,‎ 1967, p. 1001–1010 (DOI 10.4153/cjm-1967-091-8)
Lili Xiao, Dennis K. J. Lin et Fengshan Bai, « Constructing Definitive Screening Designs Using Conference Matrices », Journal of Quality Technology, vol. 44, n^o 1,‎ 2012, p. 2–8 (DOI 10.1080/00224065.2012.11917877)
D. G. Corneil et R. Mathon (éditeurs), Geometry and Combinatorics: Selected Works of J. J Seidel, Boston, Academic Press, 1991.
Yuri J. Ionin et Hadi Kharachani, « Balanced Generalized Weighing Matrices and Conference Matrices », dans Handbook of Combinatorial Designs, 2007, p. 306-309
Charles Colbourn et Jeffrey H. Dinitz, Handbook of Combinatorial Designs, Boca Raton, Chapman and Hall / CRC Press, 2007 (ISBN 1-58488-506-8).
van Lint, Jacobus Hendricus; Wilson, Richard Michael (2001) A Course in Combinatorics, Cambridge: Cambridge University Press, (ISBN 0-521-00601-5).
Stinson, Douglas Robert (2004) Combinatorial Designs: Constructions and Analysis, New York: Springer, (ISBN 0-387-95487-2) .
Eric D. Schoen, Pieter T. Eendebak, Peter Goos, « A Classification Criterion for Definitive Screening Designs », Annals of Statistics,‎ 2018.

Bibliographie complémentaire

N. A. Balonin, Jennifer Seberry, «A Review and New Symmetric Conference Matrices», Research Online, Université de Wollongong, 2014. L'annexe répertorie toutes les matrices de conférence connues et possibles jusqu'à 1002.

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.