Graphe demi-transitif
En thĂ©orie des graphes, un graphe non-orientĂ© est demi-transitif s'il est sommet-transitif et arĂȘte-transitif, mais pas symĂ©trique. Autrement dit, un graphe est demi-transitif si son groupe d'automorphismes agit transitivement sur ses sommets et ses arĂȘtes, mais pas sur ses arcs c'est-Ă -dire ses paires ordonnĂ©es de sommets adjacents[1].
| Familles de graphes définies par leurs automorphismes | ||||
|---|---|---|---|---|
| distance-transitif | â | distance-rĂ©gulier | â | fortement rĂ©gulier |
| â | ||||
| symĂ©trique (arc-transitif) | â | t-transitif, (t â„ 2) | symĂ©trique gauche (en) | |
| â | ||||
| (si connexe) sommet-transitif et arĂȘte-transitif |
â | rĂ©gulier et arĂȘte-transitif | â | arĂȘte-transitif |
| â | â | â | ||
| sommet-transitif | â | rĂ©gulier | â | (si biparti) birĂ©gulier |
| â | ||||
| graphe de Cayley | â | zĂ©ro-symĂ©trique | asymĂ©trique | |
Propriétés
Un graphe sommet-transitif et arĂȘte-transitif de degrĂ© impair est arc-transitif[2]. Il n'existe donc pas de graphe demi-transitif de degrĂ© impair.
En revanche un graphe 2k-rĂ©gulier demi-transitif peut ĂȘtre construit pour tout kâ©Ÿ2[3].
Exemples
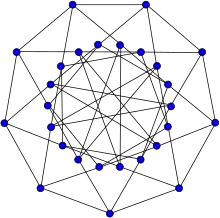
Le graphe de Doyle est le plus petit graphe demi-transitif.
Le plus petit graphe demi-transitif est le graphe de Holt (ou graphe de Doyle), un graphe 4-rĂ©gulier Ă 27 sommets et 54 arĂȘtes[1].
Notes et références
- (en) Ming-Yao Xu, « Half-Transitive Graphs of Prime-Cube Order », Journal of Algebraic Combinatorics, vol. 1, no 3,â , p. 275â282 (ISSN 1572-9192, DOI 10.1023/A:1022440002282, lire en ligne, consultĂ© le )
- (en) D MaruĆĄiÄ et R Nedela, « Maps and Half-transitive Graphs of Valency 4 », European Journal of Combinatorics, vol. 19, no 3,â , p. 345â354 (ISSN 0195-6698, DOI 10.1006/eujc.1998.0187, lire en ligne, consultĂ© le )
- (en) I. Z. Bouwer, « Vertex and Edge Transitive, but not 1-Transitive, Graphs », Canadian Mathematical Bulletin, vol. 13, no 2,â , p. 231â237 (ISSN 0008-4395 et 1496-4287, DOI 10.4153/CMB-1970-047-8, lire en ligne, consultĂ© le )
Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplĂ©mentaires peuvent sâappliquer aux fichiers multimĂ©dias.