Graphe de Doyle

Le graphe de Doyle (ou graphe de Holt) est, en théorie des graphes, un graphe 4-régulier possédant 27 sommets et 54 arêtes. C'est le plus petit graphe exemple de graphe étant sommet-transitif et arête-transitif mais pas symétrique[1] - [2]. De tels graphes sont rares[3]. Il doit son nom à Peter G. Doyle et Derek F. Holt qui le découvrirent tous deux de façon indépendante en 1976[4] et 1981[5] respectivement.

Graphe de Doyle
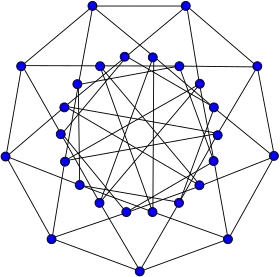Représentation du graphe de Doyle

Nombre de sommets	27
Nombre d'arêtes	54
Distribution des degrés	4-régulier
Rayon	3
Diamètre	3
Maille	5
Automorphismes	54
Nombre chromatique	3
Indice chromatique	5
Propriétés	Régulier Eulérien Hamiltonien Cayley Sommet-transitif Arête-transitif

Propriétés

Propriétés générales

Le diamètre du graphe de Doyle, l'excentricité maximale de ses sommets, est 3, son rayon, l'excentricité minimale de ses sommets, est 3 et sa maille, la longueur de son plus court cycle, est 5. Il s'agit d'un graphe 4-sommet-connexe et d'un graphe 4-arête-connexe, c'est-à-dire qu'il est connexe et que pour le rendre déconnecté il faut le priver au minimum de 4 sommets ou de 4 arêtes.

C'est également un graphe hamiltonien avec 98 472 cycles hamiltoniens distincts.

Coloration

Le nombre chromatique du graphe de Doyle est 3. C'est-à-dire qu'il est possible de le colorer avec 3 couleurs de telle façon que deux sommets reliés par une arête soient toujours de couleurs différentes mais ce nombre est minimal. Il n'existe pas de 2-coloration valide du graphe.

L'indice chromatique du graphe de Doyle est 5. Il existe donc une 5-coloration des arêtes du graphe telle que deux arêtes incidentes à un même sommet soient toujours de couleurs différentes. Ce nombre est minimal.

Propriétés algébriques

Le groupe d'automorphismes du graphe de Doyle est un groupe d'ordre 54.

Le polynôme caractéristique de la matrice d'adjacence du graphe de Doyle est : $-(x-4)(x-1)^{4}(x+2)^{4}(x^{3}-6x+2)^{6}$ .

Voir aussi

Liens internes

Théorie des graphes

Liens externes

(en) Eric W. Weisstein, Doyle Graph (MathWorld)

Références

Doyle, P. "A 27-Vertex Graph That Is Vertex-Transitive and Edge-Transitive But Not L-Transitive." October 1998.
(en) Brian Alspach, Dragan Marušič et Lewis Nowitz, « Constructing Graphs which are ½-Transitive », Journal of the Australian Mathematical Society (Series A), vol. 56, n^o 3,‎ 1994, p. 391–402 (DOI 10.1017/S1446788700035564, lire en ligne).
Jonathan L. Gross, Jay Yellen, Handbook of Graph Theory, CRC Press, 2004, (ISBN 1-58488-090-2), p. 491.
P. G. Doyle On Transitive Graphs, Senior Thesis, 1976, Harvard College.
(en) Derek F. Holt, « A graph which is edge transitive but not arc transitive », Journal of Graph Theory, vol. 5, n^o 2,‎ 1981, p. 201–204 (DOI 10.1002/jgt.3190050210).

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.