Graphe sommet-connexe
En théorie des graphes, un graphe connexe « est dit k-sommet-connexe s'il possède au moins k + 1 sommets et s'il reste encore connexe après en avoir ôté k – 1[1] ».
Définitions
Un graphe autre qu'un graphe complet est de degré de sommet-connexité k s'il est k-sommet-connexe sans être k+1-sommet-connexe, donc si k est la taille du plus petit sous-ensemble de sommets dont la suppression déconnecte le graphe[2]. Les graphes complets ne sont pas inclus dans cette version de la définition car ils ne peuvent pas être déconnectés en supprimant des sommets. Le graphe complet à n sommets est de degré de connexité n-1.
Une définition équivalente est qu'un graphe avec au moins deux sommets est k-sommet-connexe, pour chaque paire de ses sommets, il existe est k chaînes indépendantes reliant ces sommets ; c'est le théorème de Menger[3]. Cette définition produit la même réponse n − 1, pour la connexité du graphe complet Kn[2].
Un graphe 1-sommet-connexe est un appelé un graphe connexe ; un graphe 2-sommet-connexe et appelé un graphe biconnexe. Un graphe 3-connexe est aussi appelé triconnexe.
Un graphe régulier de degré k est au plus k-sommet-connexe et k-arête-connexe. S'il est effectivement k-sommet-connexe et k-arête-connexe, il est dit optimalement connecté.
Exemples
- Pour tout n, le graphe complet Kn (régulier de degré n – 1) est optimalement connecté.
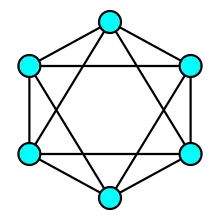
- Pour tout k > 2 et tout j > 1, le graphe moulin Wd(k, j) est 1-sommet-connexe. Pour le séparer en j composantes connexes, il suffit de supprimer son sommet de plus haut degré : son centre.
- Le graphe cycle Cn est 2-sommet-connexe pour tout n > 3.
- Le 110-graphe de Iofinova-Ivanov est 3-sommet-connexe.
 Le graphe de Biggs-Smith est 3-régulier, 3-sommet-connexe et 3-arête-connexe : il est optimalement connecté.
Le graphe de Biggs-Smith est 3-régulier, 3-sommet-connexe et 3-arête-connexe : il est optimalement connecté..svg.png.webp) Le graphe moulin Wd(5,4) n'est plus connexe si l'on supprime son sommet central: il est 1-sommet-connexe.
Le graphe moulin Wd(5,4) n'est plus connexe si l'on supprime son sommet central: il est 1-sommet-connexe.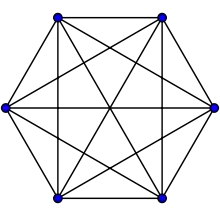 Le graphe complet K6 est 5-sommet-connexe.
Le graphe complet K6 est 5-sommet-connexe.
Nombre de graphes selon leur sommet-connexité
Nombre de graphes simples -sommet-connexes à sommets pour de 1 à 9, avec la référence à OEIS :
Nombre de graphes simples exactement -sommet-connexes à sommets:
Référence
- Matoušek Nešetřil, p. 144.
- Schrijver 2003.
- Diestel 2016.
Bibliographie
- Jiří Matoušek et Jaroslav Nešetřil, Introduction aux mathématiques discrètes, Springer, (lire en ligne)
- Reinhard Diestel, Graph Theory, Springer-Verlag, coll. « Graduate Texts in Mathematics, Volume 173 », , 5e éd., 447 p. (ISBN 978-3-662-53621-6 et 978-3-96134-005-7, lire en ligne)
- Lutz Volkmann, Fundamente der Graphentheorie, Springer, (ISBN 3-211-82774-9, lire en ligne).
- Alexander Schrijver, Combinatorial optimization : Polyhedra and efficiency, Berlin, Springer, , 1881 (3 volumes) (ISBN 978-3-540-44389-6)
Liens externes
- (en) Eric W. Weisstein, « k-Connected Graph », sur MathWorld

