Graphe eulérien

La notion de parcours eulérien s'illustre avec le problème du dessin de l'enveloppe[4]. Il s'agit de tracer une enveloppe sans lever le crayon et sans dessiner plusieurs fois un même trait. On peut modéliser le dessin avec le graphe ci-dessous. Un parcours eulérien correspond à un tracé d'un graphe sur une feuille sans lever le crayon.

• 
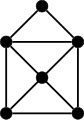  Exemple d'un graphe admettant un parcours eulérien.
• 
  Dessin à la main sans lever le crayon

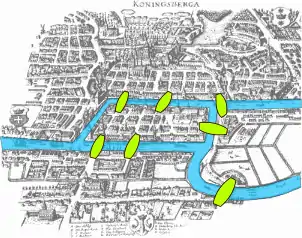
Le problème des sept ponts de Königsberg[5] est le problème de savoir si on peut traverser chaque pont de la ville de Königsberg en une promenade, une fois sur chaque pont. Comme le montre la figure ci-dessous, le problème se modélise à l'aide d'un graphe comme suit : les ponts constituent les arêtes et les îles et les berges les sommets. Comme ce graphe n'admet pas de parcours eulérien, le problème n'a pas de solutions.

On peut aussi considérer le graphe d'un polyèdre, par exemple un octaèdre. Les sommets et arêtes du polyèdre sont respectivement les sommets et arêtes du graphe.

Animation d'un des 372 circuits eulériens (de première arête donnée) du graphe des arêtes de l'octaèdre régulier. Ce graphe est eulérien car tous ses sommets sont de degré 4.

Le degré d'un sommet est le nombre d'arêtes arrivant à ce sommet (arêtes incidentes). Dans les graphes suivants, on indique les degrés pour chaque sommet.

• 
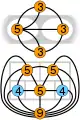  Graphe des 7 ponts de Königsberg, et un autre graphe, dit des 5 chambres. Ces graphes n'admettent pas de parcours eulériens. Les nombres indiqués sont les degrés.
• 
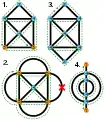  1. et 4. Graphes ayant un parcours eulérien mais pas de circuit eulérien. 2. Graphe sans solution. 3. Graphe ayant un circuit eulérien.

Le théorème d'Euler, appelé aussi théorème d'Euler-Hierholzer, se décline en deux caractérisations[5] :

• Un graphe connexe admet un parcours eulérien si et seulement si ses sommets sont tous de degré pair sauf au plus deux.
• Un graphe connexe admet un cycle eulérien si et seulement si tous ses sommets sont de degré pair.

Euler a démontré les conditions nécessaires en 1735[2]. La démonstration complète ci-dessous ayant été publiée par le mathématicien allemand Carl Hierholzer en 1873[6]. On attribue parfois l'équivalence à Euler, comme dans le livre de théorie des graphes de Diestel (voir Th. 1.8.1 dans [7]). Les deux sens directs se démontrent comme suit.

Supposons qu'il y a un parcours eulérien et empruntons le en supprimant les arêtes utilisées. À chaque passage sur un sommet (sauf au début et à la fin), on supprime l'arête qui arrive sur ce sommet et l'arête qui en part. Ainsi, sauf pour le sommet de départ ou d'arrivée, la parité du degré reste inchangée. À la fin du parcours, toutes les arêtes sont supprimées, ce qui permet de conclure sur la parité des sommets.

Les sens indirects, i.e. les réciproques, se démontrent comme suit.

Montrons le quand tous les sommets sont de degré pair. Commençons à un sommet quelconque s₀ du graphe. Empruntons des arêtes, en les supprimant du graphe, tant que cela est possible. Comme les degrés sont pairs, nous sommes forcément revenus au sommet s₀ et nous avons trouvé un circuit s₀ - s₁ - ... - s₀. S'il ne reste plus d'arêtes, alors nous avons un circuit eulérien. Sinon, nous recommençons le processus afin d'exhiber un autre circuit, depuis un sommet s_i duquel part une arête. Nous obtenons alors un autre circuit s_i - ... - s_i, que nous venons coller dans le circuit précédent à la place de s_i :

s₀ - s₁ - ... - s_i -- ... -- s_i - s_i+1 - ... s₀.

On répète le processus jusqu'à avoir utilisé toutes les arêtes et l'on obtient un circuit eulérien.

On peut effectivement écrire un programme informatique pour calculer un chemin ou un circuit eulérien s'il en existe. Discutons l'algorithme du papier de Hierholzer de 1873[6], qui suit l'idée de sa démonstration (voir le sens indirect ci-dessus). Il répète l'extraction de circuits que l'on colle pour construire un circuit eulérien[8]. Cet algorithme peut s'implémenter afin d'avoir un algorithme en temps linéaire en le nombre d'arêtes (voir Example 2.5.2, et Algorithm 2.3.1 dans [9]). Pour cela, il suffit que les opérations suivantes s'exécutent en temps constant :

1. trouver une arête non empruntée
2. trouver un nouveau sommet qui admet encore des arêtes incidentes non empruntés
3. coller le circuit dans le parcours en cours de construction

Pour cela, il suffit de maintenir efficacement avec des listes doublement chainées :

1. la liste des sommets du parcours en construction qui ont encore des arêtes inutilisées
2. pour chaque sommet, la liste des arêtes non encore utilisées
3. la liste des arêtes du parcours en construction

Pierre-Henry Fleury[10] a donné un autre algorithme en 1883 mais dont une implémentation sur ordinateur serait moins efficace que l'algorithme de Hierholzer. Son idée est de construire le circuit en empruntant à chaque fois en priorité une arête dont la suppression ne déconnecte pas le graphe.

• Problème du postier chinois (qui consiste à chercher un chemin passant au moins une fois par chaque arête)

• Théorème de BEST, qui donne une formule pour compter le nombre de circuits eulériens d'un graphe
• Liste de sujets portant le nom d'Euler

• (en) Reinhard Diestel, Graph Theory [détail des éditions]
• Édouard Lucas, Récréations mathématiques, 9 rue de Médicis, Paris, Librairie Albert Banchard, 1892 (lire en ligne) lire en ligne sur Gallica, voir p. « page 33 » où le problème est décrit sous le titre Les ponts de Paris en 1880.