Graphe arĂȘte-transitif
En thĂ©orie des graphes, un graphe non-orientĂ© est arĂȘte-transitif si pour tout couple d'arĂȘtes, il existe un automorphisme de graphe envoyant la premiĂšre arĂȘte sur la seconde.
| Familles de graphes définies par leurs automorphismes | ||||
|---|---|---|---|---|
| distance-transitif | â | distance-rĂ©gulier | â | fortement rĂ©gulier |
| â | ||||
| symĂ©trique (arc-transitif) | â | t-transitif, (t â„ 2) | symĂ©trique gauche (en) | |
| â | ||||
| (si connexe) sommet-transitif et arĂȘte-transitif |
â | rĂ©gulier et arĂȘte-transitif | â | arĂȘte-transitif |
| â | â | â | ||
| sommet-transitif | â | rĂ©gulier | â | (si biparti) birĂ©gulier |
| â | ||||
| graphe de Cayley | â | zĂ©ro-symĂ©trique | asymĂ©trique | |
DĂ©finitions
Un graphe non-orientĂ© est arĂȘte-transitif si pour tout couple d'arĂȘtes, il existe un automorphisme de graphe envoyant la premiĂšre arĂȘte sur la seconde[1] - [2]. En d'autres termes, un graphe est arĂȘte-transitif si son groupe d'automorphismes agit transitivement sur l'ensemble de ses arĂȘtes.
De maniĂšre informelle, cette propriĂ©tĂ© signifie que toutes les arĂȘtes jouent le mĂȘme rĂŽle dans le graphe.
Propriétés
Tout graphe biparti complet est arĂȘte-transitif[1].
Si un graphe connexe est arĂȘte-transitif mais pas sommet-transitif, il est biparti[1].
Un graphe connexe est arĂȘte-transitif si et seulement si son line graph est sommet-transitif[2].
Exemples
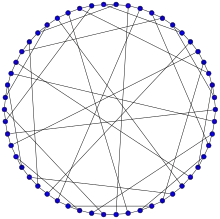
Le graphe de Gray est semi-symĂ©trique, c'est-Ă -dire arĂȘte-transitif et rĂ©gulier mais pas sommet-transitif[3].
Notes et références
- (en) Norman Biggs, Algebraic Graph Theory, 2d Edition, Cambridge University Press, , 214 p. (ISBN 978-0-521-45897-9, lire en ligne), p. 115-116
- (en) Eric W. Weisstein, « Edge-Transitive Graph », sur mathworld.wolfram.com (consulté le )
- (en) Dragan MaruĆĄiÄ, TomaĆŸ Pisanski et Steve Wilson, « The genus of the GRAY graph is 7 », European Journal of Combinatorics, topological Graph Theory and Graph Minors, second issue, vol. 26, no 3,â , p. 377â385 (ISSN 0195-6698, DOI 10.1016/j.ejc.2004.01.015, lire en ligne, consultĂ© le )