Line graph

La figure suivante illustre un graphe (à gauche, avec des sommets bleus) et son line graph (à droite, avec des sommets verts). Chaque sommet du line graph est étiqueté avec les extrémités de l'arête correspondante dans le graphe d'origine.

• 
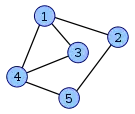  Graphe G
• 
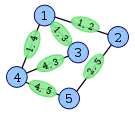  Sommets de L(G) construits à partir des arêtes de G
• 
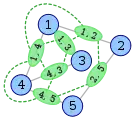  Ajout des arêtes de L(G)
• 
  Le line graph L(G)

• Le graphe de Petersen est le graphe complémentaire du line graph du graphe complet ${\displaystyle K_{5}}$.
• Le line graph du graphe tétraédrique est le graphe octaédrique.
• Le line graph du graphe hexaédrique est le graphe cuboctaédrique.
• Le line graph du graphe dodécaédrique est le graphe icosaédrique.

Les propriétés d'un graphe G dépendant uniquement de l'adjacence entre arêtes peuvent être traduites sur L(G) en propriétés équivalentes dépendant de l'adjacence entre sommets. Par exemple, un couplage dans G, c'est-à-dire un ensemble d'arêtes qui n'ont pas de sommet en commun, correspond à un ensemble de sommets deux à deux non adjacents dans L(G), donc à un stable de L(G).

En conséquence, on a les propriétés suivantes :

• Le line graph d'un graphe connexe est connexe. La réciproque n'est cependant pas vraie. Un graphe G ayant des sommets isolés peut avoir un line graph connexe.
• Un ensemble stable de poids maximal dans un line graph L(G) correspond à un couplage maximum dans G. Comme un couplage maximum peut être trouvé en temps polynomial, la recherche d'un ensemble stable de poids maximal se fait également en temps polynomial dans un line graph, même s'il s'agit dans le cas général d'un problème NP-complet au sens de la théorie de la complexité.
• L'indice chromatique d'un graphe G est égal au nombre chromatique de son line graph L(G). En effet, colorer les arêtes d'un graphe équivaut à colorer les sommets de son line graph.
• Le line graph d'un graphe sommet-transitif est un graphe arête-transitif.
• Si un graphe G a un cycle eulérien, c'est-à-dire si G est connexe et que tous ses sommets sont de degré pair, alors le line graph L(G) est un graphe hamiltonien. Il peut exister cependant des cycles hamiltoniens dans L(G) qui ne proviennent pas de cycles eulériens dans G.

Les line graphs sont des graphes sans griffe, c'est-à-dire des graphes qui n'admettent pas le graphe griffe comme sous-graphe induit.

Le line graph d'un graphe biparti est un graphe parfait (voir le théorème de König). Les line graphs des graphes bipartis sont utilisés dans la preuve du théorème des graphes parfaits.

Les neuf graphes minimaux n'étant pas des line graphs, tirés de la caractérisation par de Beineke des line graphs par sous-graphes interdits. Un graphe est un line graphe si et seulement s'il n'admet aucun de ces neuf graphes comme sous-graphe induit.

Un graphe G est le line graph d'un autre graphe, si et seulement s'il est possible de trouver un ensemble de cliques dans G qui partitionne les arêtes de G tel que chaque sommet de G appartienne exactement à deux des cliques. Certaines de ces cliques peuvent être réduites à un seul sommet.

Par un résultat de Hassler Whitney[2], si G n'est pas un triangle, alors il ne peut y avoir qu'une seule partition de ce type. Si une telle partition existe, il est possible de retrouver le graphe d'origine dont G est le line graph. Pour cela, il suffit de créer un sommet pour chaque clique et de relier par des arêtes les couples de cliques qui partagent un sommet en commun dans G. Roussopoulos utilisa en 1973 ce résultat comme base pour construire une algorithme permettant d'identifier les 'line graphs en temps linéaire[5].

Un corollaire de ce résultat est que, exception faite des cas du graphe complet ${\displaystyle K_{3}}$ et du graphe biparti complet ${\displaystyle K_{1,3}}$, si les line graphs L(G) et L(H) de deux graphes G et H sont isomorphes, alors les graphes G et H sont isomorphes.

Une autre caractérisation des line graphs fut proposée par Beineke en 1968[6] (puis prouvée en 1970[7]). Il montra qu'il existait neuf graphes minimaux qui n'étaient pas des line graphs tel que tout graphe n'étant pas un line graph avait pour sous-graphe induit au moins un de ces graphes minimaux.

En 1965, van Rooij et Wilf s'intéressent à l'itération de l'opérateur line graph[8]. Considérons la séquence suivante :

${\displaystyle G,L(G),L(L(G)),L(L(L(G))),\dots .\ }$

Alors, si G est un graphe connexe fini, seuls quatre comportements différents sont possibles pour cette séquence :

• Si G est un graphe cycle alors L(G) ainsi que chaque graphe de la séquence est un graphe isomorphe à G lui-même. Les graphes cycles sont les seuls graphes connexes à être isomorphes à leur line graph.
• Si G est le graphe griffe K_1,3, alors L(G) et tous les graphes qui suivent dans la séquence sont des graphes triangles (donc des graphes cycles de longueur 3).
• Si G est un graphe chemin, alors chaque graphe qui suit dans la séquence est un chemin plus court jusqu'à terminer avec le graphe singleton et enfin le graphe nul.
• Dans tous les autres cas, la taille des graphes de la séquence augmente sans être bornée.

Si G n'est pas connexe, alors cette classification s'applique séparément à chaque composante connexe de G.