Graphe tétraédrique
Le graphe tétraédrique est, en théorie des graphes, un graphe 3-régulier possédant 4 sommets et 6 arêtes. C'est le squelette du tétraèdre régulier, un solide de Platon ayant 4 faces, toutes triangulaires.
| Graphe tétraédrique | |
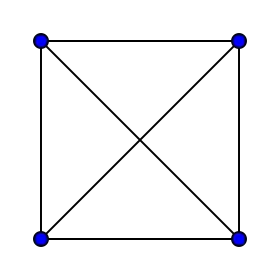 Représentation du graphe tétraédrique. | |
| Nombre de sommets | 4 |
|---|---|
| Nombre d'arêtes | 6 |
| Distribution des degrés | 3-régulier |
| Rayon | 1 |
| Diamètre | 1 |
| Maille | 3 |
| Automorphismes | 24 |
| Nombre chromatique | 4 |
| Indice chromatique | 3 |
| Propriétés | Arête-transitif Complet Cubique Distance-régulier Fortement régulier Hamiltonien Parfait Planaire Régulier Sommet-transitif Symétrique Intégral |
Construction
Il existe cinq graphes correspondant aux squelettes des cinq solides de Platon. Le graphe tétraédrique est l'un d'eux. Les quatre autres sont le graphe hexaédrique, le graphe octaédrique, le graphe dodécaédrique et le graphe icosaédrique.
Le graphe tétraédrique est également isomorphe au graphe complet K4 et au graphe roue W4.
Le line graph du graphe tétraédrique est le graphe octaédrique.
Propriétés
Propriétés générales
Le diamètre du graphe tétraédrique, l'excentricité maximale de ses sommets, est 1 ainsi que son rayon, l'excentricité minimale de ses sommets. Tous ses sommets appartiennent donc à son centre.
La maille du graphe tétraédrique, la longueur de son plus court cycle, est 3. Il s'agit d'un graphe 3-sommet-connexe et d'un graphe 3-arête-connexe, c'est-à-dire qu'il est connexe et que pour le rendre déconnecté il faut le priver au minimum de 3 sommets ou de 3 arêtes.
Le graphe tétraédrique contient 14 cycles distincts (7 sans tenir compte du sens de parcours). Six d'entre eux sont des cycles hamiltoniens (3 sans tenir compte du sens de parcours). Il contient également 24 chemins hamiltoniens.
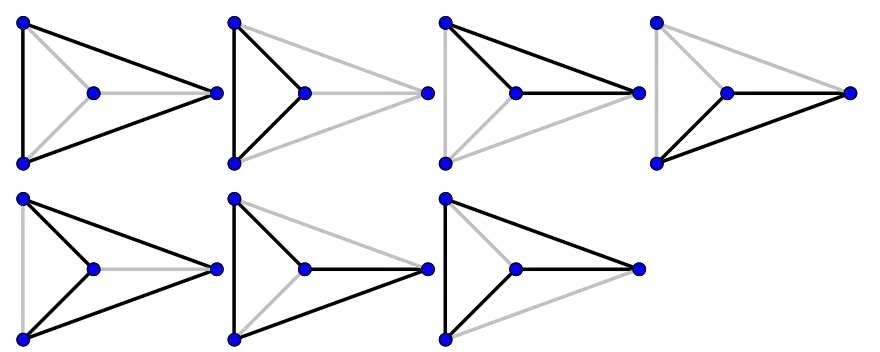
Coloration
Le nombre chromatique du graphe tétraédrique est 4. C'est-à-dire qu'il est possible de le colorer avec 4 couleurs de telle façon que deux sommets reliés par une arête soient toujours de couleurs différentes. Ce nombre est minimal.
L'indice chromatique du graphe tétraédrique est 3. Il existe donc une 3-coloration des arêtes du graphe telle que deux arêtes incidentes à un même sommet soient toujours de couleurs différentes. Ce nombre est minimal.
Il est possible de compter les colorations distinctes d'un graphe. Cela donne une fonction dépendant du nombre de couleurs autorisé. Cette fonction est polynomiale et est qualifiée de polynôme chromatique du graphe. Ce polynôme a pour racines tous les entiers positifs ou nuls strictement inférieurs à 4 et est de degrés 4. Il est égal à : .

Propriétés algébriques
Le graphe tétraédrique est symétrique, c'est-à-dire que son groupe d'automorphismes agit transitivement sur ses arêtes, ses sommets et ses arcs. Il est donc également arête-transitif et sommet-transitif. Le graphee tétraédrique est l'unique graphe cubique symétrique à 4 sommets et sa notation dans le Foster Census, le catalogue classifiant tous les graphes cubiques symétriques, est F4A[1]. C'est le plus petit graphe cubique symétrique[2].
Le groupe d'automorphismes du graphe tétraédrique est d'ordre 24.
Le polynôme caractéristique de la matrice d'adjacence du graphe tétraédrique est : . Il n'admet que des racines entières ; le graphe tétraédrique est donc un graphe intégral, un graphe dont le spectre est constitué d'entiers.
Voir aussi
Liens internes
Liens externes
Références
- (en) Conder, M. and Dobcsányi, P. "Trivalent Symmetric Graphs Up to 768 Vertices." J. Combin. Math. Combin. Comput. 40, 41-63, 2002
- (en) Royle, G. "Cubic Symmetric Graphs (The Foster Census)."

