Graphe de Gray
Le graphe de Gray est, en théorie des graphes, un graphe 3-régulier possédant 54 sommets et 81 arêtes.
| Graphe de Gray | |
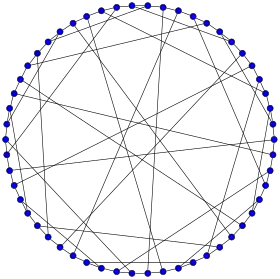 Représentation du graphe de Gray. | |
| Nombre de sommets | 54 |
|---|---|
| Nombre d'arêtes | 81 |
| Distribution des degrés | 3-régulier |
| Rayon | 6 |
| Diamètre | 6 |
| Maille | 8 |
| Automorphismes | 1 296 |
| Nombre chromatique | 2 |
| Indice chromatique | 3 |
| Propriétés | Cubique Semi-symétrique Hamiltonien |
Il tire son nom de Marion Cameron Gray qui le découvrit en 1932 ; il fut publié pour la première fois par I. Z. Bouwer en 1968[1].
Propriétés
Propriétés générales
Le diamètre du graphe de Gray, l'excentricité maximale de ses sommets, est 6, son rayon, l'excentricité minimale de ses sommets, est 6 et sa maille, la longueur de son plus court cycle, est 8. Il s'agit d'un graphe 3-sommet-connexe et d'un graphe 3-arête-connexe, c'est-à-dire qu'il est connexe et que pour le rendre déconnecté il faut le priver au minimum de 3 sommets ou de 3 arêtes.
Coloration
Le nombre chromatique du graphe de Gray est 2. C'est-à-dire qu'il est possible de le colorer avec 2 couleurs de telle façon que deux sommets reliés par une arête soient toujours de couleurs différentes. Ce nombre est minimal.
L'indice chromatique du graphe de Gray est 3. Il existe donc une 3-coloration des arêtes du graphe telle que deux arêtes incidentes à un même sommet soient toujours de couleurs différentes. Ce nombre est minimal.
Propriétés algébriques
Le groupe d'automorphismes du graphe de Gray est un groupe d'ordre 1 296. Il agit transitivement sur l'ensemble des arêtes du graphe de Gray, faisant de lui un graphe arête-transitif, c'est-à-dire un graphe dont toutes les arêtes jouent exactement le même rôle. Cependant il n'agit pas transitivement sur l'ensemble de ses sommets. Le graphe de Gray étant régulier, il est un exemple de graphe semi-symétrique : un graphe régulier arête-transitif mais pas sommet-transitifs. C'est le plus petit graphe cubique vérifiant cette propriété.
Le polynôme caractéristique de la matrice d'adjacence du graphe de Gray est : . Le graphe de Gray est déterminé de façon unique par son spectre de graphe, l'ensemble des valeurs propres de sa matrice d'adjacence.
Voir aussi
Liens internes
Liens externes
- (en) Eric W. Weisstein, Gray Graph (MathWorld)
- (en) Andries E. Brouwer, Gray graph
Références
- I. Z. Bouwer, An edge but not vertex transitive cubic graph, Bulletin of the Canadian Mathematical Society no 11 (1968) p. 533-535.
