Produit en couronne

Pour un ensemble X, nous désignerons ici par S_X et nous appellerons groupe symétrique de X l'ensemble des permutations de X, muni de la loi de groupe ∘ définie par f ∘ g : X → X : x ↦ f(g(x)). Cette définition convient à l'étude des actions à gauche d'un groupe sur un ensemble. Le groupe opposé du groupe noté ici S_X convient à l'étude des actions à droite. Quand nous parlerons d'une action d'un groupe sur un ensemble, il s'agira d'une action à gauche. On sait qu'à une action à gauche d'un groupe G sur un ensemble X correspond naturellement un homomorphisme de groupes de G dans S_X si bien qu'on peut voir l'un comme l'autre et vice-versa.
Pour une permutation α d'un ensemble X et un élément x de X, il nous arrivera d'écrire αx au lieu de α(x). Pour deux permutations α et β d'un même ensemble E, il nous arrivera d'écrire αβ au lieu de α ∘ β, ce qui revient à noter multiplicativement le groupe S_E.
On dira qu'une famille ${\displaystyle \ (a_{y})_{y\in Y}}$ d'éléments d'un groupe G est de support fini si les éléments y de Y tels que a_y ≠ 1 sont en nombre fini. Une telle famille est une application de Y dans (l'ensemble sous-jacent à) G. Autrement dit on dira qu'une application f de Y dans G est de support fini si les éléments y de Y tels que f(y) ≠ 1 sont en nombre fini.
Si G est un groupe et Y un ensemble, on notera G^Y le produit direct (externe) de la famille, indexée par Y, de groupes tous égaux à G. Donc G^Y a pour éléments les familles, indexées par Y, d'éléments de G et est donc le groupe des applications de Y dans G, la loi de groupe étant la «multiplication terme à terme».
On notera G^(Y) la somme restreinte (externe) de la même famille, indexée par Y, de groupes tous égaux à G. Donc G^(Y) a pour éléments les familles de support fini, indexées par Y, d'éléments de G et est donc le groupe des applications à support fini de Y dans G, la loi de groupe étant toujours la «multiplication terme à terme». Si l'ensemble Y est fini, le produit direct et la somme restreinte sont identiques.
G étant un groupe, nous noterons λ(G) l'image de G par l'homomorphisme

${\displaystyle \lambda :G\rightarrow S_{G}:g\mapsto \lambda _{g}:h\mapsto :gh}$

de ${\displaystyle \ G}$ dans ${\displaystyle \ S_{G}}$. Pour un élément g de G, λ_g est la translation à gauche par g dans G. Donc λ(G) est un groupe de permutations de (l'ensemble sous-jacent de) G et, d'après le théorème de Cayley, le groupe λ(G) est isomorphe à G.
Pour un groupe G, nous appellerons action régulière de G l'action de G sur son ensemble sous-jacent par translations à gauche.

Soient G un groupe de permutations d'un ensemble X non vide et H un groupe de permutations d'un ensemble Y non vide.

Pour tout élément ${\displaystyle \ \gamma }$ de S_X et tout élément y de Y, convenons de noter ${\displaystyle \ \gamma _{Y,y}}$ la permutation de l'ensemble X × Y (produit cartésien) définie comme suit : pour tout élément x de X et tout élément y' de Y,

${\displaystyle \ \gamma _{Y,y}(x,y')=(\gamma x,y)}$ si y' = y;

${\displaystyle \ \gamma _{Y,y}(x,y')=(x,y')}$ si y' ≠ y.

Pour tout élément η de S_Y, convenons de noter ${\displaystyle \eta _{X}^{*}}$ la permutation de l'ensemble X × Y définie comme suit :

${\displaystyle \eta _{X}^{*}(x,y)=(x,\eta (y)).}$

(Les notations ${\displaystyle \ \gamma _{Y,y}}$ et ${\displaystyle \eta _{X}^{*}}$ ne sont pas standard.)

Pour tout élément y de Y, ${\displaystyle \ \gamma \mapsto \gamma _{Y,y}}$ définit un homomorphisme injectif du groupe G dans le groupe S _{X × Y}. Si nous désignons par ${\displaystyle G_{Y,y}}$ l'image de G par cet homomorphisme, ${\displaystyle \ \gamma \mapsto \gamma _{Y,y}}$ définit donc un isomorphisme du groupe G sur le sous-groupe G_Y,y de S _{X × Y}.
De même, ${\displaystyle \eta \mapsto \eta _{X}^{*}}$ définit un isomorphisme du groupe H sur un sous-groupe de S _{X × Y}, sous-groupe que nous noterons ${\displaystyle \ H_{X}^{*}.}$

Le produit en couronne de G et H (ou de G par H) est par définition[1] le sous-groupe de S_X×Y engendré par les ${\displaystyle G_{Y,y}}$, où y parcourt Y, et ${\displaystyle \ H_{X}^{*}.}$ On le note souvent G ≀ H, mais il existe d'autres notations. Nous conviendrons de n'utiliser ici que la notation G ≀ H, réservant d'autres notations à des versions du produit en couronne qui seront présentées plus loin.

Soient G, H des groupes de permutations d'ensembles non vides. On vérifie facilement la propriété suivante :

• Si G et H sont transitifs, G ≀ H est transitif[2].

On a également une propriété de quasi-associativité :

• Si G, H et K sont trois groupes de permutations d'ensembles non vides, les groupes de permutations (G ≀ H) ≀ K et G ≀ (H ≀ K) sont semblables[3].

Plus précisément, si G, H et K sont respectivement des groupes de permutations de X, de Y et de Z, si f désigne la bijection ((x, y), z) ↦ (x, (y, z)) de (X × Y) × Z sur X × (Y × Z), si f* désigne l'isomorphisme s ↦ f ∘ s ∘ f⁻¹ de S_{(X × Y) × Z} sur S_{X × (Y × Z)}, alors G ≀ (H ≀ K) est l'image de (G ≀ H) ≀ K par f*.

Dans les hypothèses ci-dessus sur G et sur H, le sous-groupe B de G ≀ H engendré par les ${\displaystyle G_{Y,y}}$, où y parcourt Y, est appelé le groupe de base du produit en couronne G ≀ H. Donc G ≀ H est engendré par B et par ${\displaystyle \ H_{X}^{*}}$.
Si ${\displaystyle \ \gamma }$ est un élément de G et y un élément de Y, si η est un élément de H, alors

${\displaystyle \ (1)\qquad \eta _{X}^{*}\circ \gamma _{Y,y}\circ \eta _{X}^{*^{-1}}=\gamma _{Y,\eta y}}$

d'où on tire que B est normal dans G ≀ H et que G ≀ H est produit semi-direct interne ${\displaystyle \ B\rtimes H_{X}^{*}}$ de B par ${\displaystyle \ H_{X}^{*}.}$

On vérifie que les sous-groupes ${\displaystyle G_{Y,y}}$, où y parcourt Y, sont en somme restreinte, c'est-à-dire que B est somme restreinte interne de la famille ${\displaystyle (G_{Y,y})_{y\in Y}.}$ Donc, étant donné une famille de support fini ${\displaystyle (\gamma _{y})_{y\in Y}}$ d'éléments de G, on peut définir sans ambiguïté

${\displaystyle \ \prod _{y\in Y}(\gamma _{y})_{Y,y},}$

où le produit correspond à la loi de groupe de S _{X × Y}. De plus,

${\displaystyle \ (\gamma _{y})_{y}\mapsto \prod _{y\in Y}(\gamma _{y})_{Y,y}}$

définit un isomorphisme de G^(Y) sur B.

Il résulte de ce qui précède que si Y est fini, l'ordre de G ≀ H est donné par

${\displaystyle \ (2)\qquad \vert G\wr H\vert =\vert G\vert ^{\vert Y\vert }\vert H\vert .}$

Si G et H sont deux groupes quelconques (qu'on ne suppose pas opérer sur des ensembles), on appelle produit en couronne régulier[4] de G par H le produit en couronne λ(G) ≀ λ(H) (où λ est défini comme dans la section Conventions). On le note parfois ${\displaystyle G\ _{r}^{\wr }H}$. On observera[5] que, contrairement à ce qui est le cas du produit en couronne ≀ , ${\displaystyle \ (G\ _{r}^{\wr }H)\ _{r}^{\wr }K}$ n'est pas forcément isomorphe comme groupe à ${\displaystyle \ G\ _{r}^{\wr }(H\ _{r}^{\wr }K).}$ (On le tire facilement de la formule (2) donnant l'ordre du produit en couronne G ≀ H quand Y est fini.)

Soit G un groupe, soit H un groupe opérant sur un ensemble non vide Y. Dans la définition du produit en couronne restreint ${\displaystyle \ G\ _{w}H}$, rien n'empêche de remplacer la somme restreinte G^(Y) par le produit direct G^Y et l'action par décalage de H sur G^(Y) par l'action par décalage de H sur G^Y :

${\displaystyle \ H\times G^{Y}\rightarrow G^{Y}:(\eta ,(\gamma _{y})_{y\in Y})\mapsto (\gamma _{\eta ^{-1}y})_{y\in Y}.}$

On obtient ainsi la définition suivante[6] :

pour un groupe G et pour un groupe H opérant sur un ensemble Y, le produit en couronne complet de G par H (relativement à l'action en question de H sur Y) est le produit semi-direct externe G^Y ⋊ H de G^Y par H relativement à l'action par décalage de H sur G^Y.

Nous noterons ${\displaystyle \ G\ _{W}H}$ ce produit en couronne complet. Le produit en couronne restreint ${\displaystyle \ G\ _{w}H}$ est sous-groupe de ${\displaystyle \ G\ _{W}H}$. Si l'ensemble Y est fini, ${\displaystyle \ G\ _{w}H}$ et ${\displaystyle \ G\ _{W}H}$ sont identiques.

On ne peut pas calquer sur le cas restreint une « version permutationnelle » du produit en couronne complet, car si une famille d'éléments d'un groupe n'est pas de support fini, le produit de cette famille d'éléments n'est pas défini.

• (Kaloujnine[9]) Soient p un nombre premier et r un nombre naturel. Les p-sous-groupes de Sylow de ${\displaystyle \ S_{p^{r}}}$ sont isomorphes au produit en couronne itéré

${\displaystyle \lambda (\mathbb {Z} /p\mathbb {Z} )\wr \ldots \lambda (\mathbb {Z} /p\mathbb {Z} )}$

de r groupes de permutations égaux à ${\displaystyle \lambda (\mathbb {Z} /p\mathbb {Z} )}$. (Vu la quasi-associativité de ≀, il n'est pas nécessaire de préciser un parenthésage du produit en couronne itéré.)

Plus généralement, si p est un nombre premier, si n est un nombre naturel, si l'écriture de n en base p est a₀ + a₁ p + ... + a_r p^r, si nous désignons par W(s, p) le produit en couronne itéré de s groupes de permutations égaux à ${\displaystyle \lambda (\mathbb {Z} /p\mathbb {Z} )}$, alors les p-sous-groupes de Sylow de S_n sont isomorphes au produit direct de a₁ copies de W(1, p), de a₂ copies de W(2, p), ... et de a_r copies de W(r, p).

• On entendra ici par « graphe » un graphe non orienté (au sens de la théorie des graphes).

Considérons d'abord le graphe obtenu comme suit.

• 
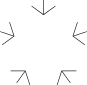  Graphe Γ
• 
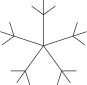  Graphe Γ₁
• 
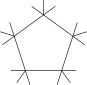  Graphe Γ₂

On représente les 5 sommets d'un pentagone régulier et à partir de chaque sommet, on trace vers l'extérieur du pentagone 3 segments fermés, en veillant à ce que deux segments fermés issus de deux sommets distincts n'aient jamais de point commun. (Les nombres 5 et 3 sont en fait arbitraires.) On prend pour sommets du graphe les sommets du pentagone et les autres extrémités des segments. On prend pour arêtes du graphe les segments. On obtient ainsi un graphe Γ à 5 composantes connexes. Ces composantes connexes sont toutes isomorphes à un graphe dont le groupe des automorphismes est isomorphe à S₃. On montre que, pour toute permutation s des 5 sommets du pentagone, il existe 3⁵ automorphismes du graphe Γ qui permutent ces 5 sommets de la même façon que s, et que le groupe des isomorphismes de Γ est isomorphe à S₃ ≀ S₅.

Cela peut être ramené au fait général suivant[10] : si E est un ensemble, si ${\displaystyle \ (F_{i})_{i\in I}}$ est une partition de E en ensembles tous équipotents à un même ensemble F, les permutations f de E telles que, pour tout élément i de I, il existe un élément j de I satisfaisant à ${\displaystyle \ f(F_{i})=F_{j}}$ (autrement dit les permutations de E qui permutent les E_i entre eux) forment un sous-groupe de S_E isomorphe à ${\displaystyle \ S_{F}\ _{W}S_{I}}$ (défini relativement à l'opération naturelle de ${\displaystyle \ S_{I}}$).

La non-connexité du graphe Γ n'est évidemment pas essentielle : si aux sommets de Γ, on ajoute le centre du pentagone et qu'aux arêtes du graphe, on ajoute les segments joignant le centre aux sommets du pentagone, on obtient un graphe Γ₁, cette fois-ci connexe, dont le groupe des automophismes est lui aussi[11] isomorphe à S₃ ≀ S₅.

Reprenons le graphe (non connexe) Γ et ajoutons à ses arêtes les 5 côtés du pentagone. Soit Γ₂ le graphe ainsi obtenu. Contrairement à ce qui était le cas de Γ, un automorphisme de Γ₂ ne peut pas permuter de façon quelconque les 5 sommets du pentagone, il doit les permuter à la façon d'une rotation. On montre[12] que le groupe des automorphismes de Γ₂ est isomorphe à ${\displaystyle \ S_{3}\wr \lambda (\mathbb {Z} /5\mathbb {Z} ).}$

• Soient G un groupe abélien non trivial (par trivial, on entend ici réduit à l'élément neutre) et H un groupe opérant fidèlement et transitivement sur un ensemble non vide Y, soit ${\displaystyle \ G\ _{w}H}$ le produit en couronne restreint correspondant, soit B le groupe de base. On montre que le centre de ${\displaystyle \ G\ _{w}H}$ est le sous-groupe de B formé par les couples (f, 1), où f parcourt les applications de Y dans G qui sont à la fois constantes et de support fini. Si Y est infini, une application de support fini de Y dans G ne peut être constante que si elle a partout la valeur 1, donc, dans le cas où Y est infini, le centre de ${\displaystyle \ G\ _{w}H}$ est réduit à l'élément neutre.

Soit p un nombre premier. Nous pouvons choisir un p-groupe infini K (par exemple le p-groupe de Prüfer, ou encore le produit direct ou la somme directe d'une famille infinie de groupes d'ordre p). Prenons pour Y l'ensemble sous-jacent de K et pour H le groupe λ(K) opérant naturellement sur Y = K; prenons pour G un groupe d'ordre p. D'après ce qui précède, le centre de ${\displaystyle \ G\ _{w}H}$ est réduit à l'élément neutre. Or la somme restreinte d'une famille (finie ou infinie) de p-groupes est un p-groupe et un produit semi-direct de deux p-groupes est un p-groupe, donc ${\displaystyle \ G\ _{w}H}$ est un p-groupe. Ceci montre que, contrairement aux p-groupes finis non triviaux, un p-groupe infini peut avoir un centre trivial[13].

• Le produit en couronne restreint ${\displaystyle \ \mathbb {Z} \ _{w}\lambda (\mathbb {Z} )}$ (correspondant à l'action naturelle de ${\displaystyle \ \lambda (\mathbb {Z} )}$) est engendré par les deux éléments (f₁, 0) et (0, λ₁), où f₁ désigne l'application de Z dans Z nulle partout sauf en 1 où elle vaut 1, et où λ₁ désigne la translation x ↦ x + 1 dans Z. D'autre part, le groupe de base de ce produit en couronne n'est pas de type fini, car la somme restreinte d'une famille infinie de groupes tous non triviaux n'est pas un groupe de type fini. Ceci montre qu'un sous-groupe d'un groupe de type fini n'est pas forcément de type fini[14].

Remarque : au lieu du groupe λ(Z) et de son action naturelle, on aurait pu considérer le groupe Z et son action régulière.

• Soit W le produit en couronne complet

${\displaystyle \ W=\mathbb {Z} /2\mathbb {Z} \ _{W}\mathbb {Z} }$

relativement à l'action régulière de ${\displaystyle \ \mathbb {Z} }$

W est donc le produit semi-direct de ${\displaystyle \ (\mathbb {Z} /2\mathbb {Z} )^{\mathbb {Z} }}$ par ${\displaystyle \ \mathbb {Z} }$ relativement à l'action de ${\displaystyle \ \mathbb {Z} }$ sur ${\displaystyle \ (\mathbb {Z} /2\mathbb {Z} )^{\mathbb {Z} }}$ par décalage :

${\displaystyle \ \mathbb {Z} \times (\mathbb {Z} /2\mathbb {Z} )^{\mathbb {Z} }\rightarrow (\mathbb {Z} /2\mathbb {Z} )^{\mathbb {Z} }:(k,(u_{n})_{n\in \mathbb {Z} })\mapsto (u_{n-k})_{n\in \mathbb {Z} }}$

Désignons par V₀ le sous-groupe de ${\displaystyle \ (\mathbb {Z} /2\mathbb {Z} )^{\mathbb {Z} }}$ formé par les familles nulles en tout indice strictement négatif. Soit V le sous-groupe V₀ × {0} de W. Pour tout entier rationnel k, le sous-groupe (0,k) V (0, k)^-1 de W (où 0 désigne la famille nulle partout) est formé par les familles qui sont nulles en tout n < k. Donc si k > 0, alors (0,k) V (0, k)^-1 est strictement contenu dans V. Ceci montre qu'un conjugué d'un sous-groupe peut être strictement contenu dans ce sous-groupe[15]. Donc pour qu'un élément x d'un groupe G normalise un sous-groupe H de G, il ne suffit pas toujours que xHx^-1 soit contenu dans H.

Marc Krasner et Lev Kloujnine (en) ont démontré en 1951[16] que si K et Q sont des groupes, toute extension de K par Q est isomorphe à un sous-groupe du produit en couronne complet de K par Q relativement à l'action régulière de Q[17].

La notion de produit en couronne peut s'étendre de plusieurs façons des groupes aux demi-groupes[18]. .

• John D. P. Meldrum, Wreath Products of Groups and Semigroups, Chapman & Hall/CRC, 1995 (ISBN 9780582026933)