Lois de Kirchhoff

Schéma d'un montage électrique illustrant la loi des nœuds.

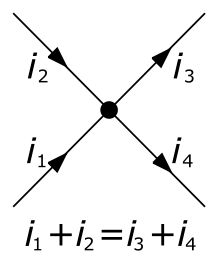
La somme des intensités des courants qui entrent par un nœud est égale à la somme des intensités des courants qui sortent du même nœud[1].

Sur la figure est représenté le sens (choisi arbitrairement) d'orientation de chaque fil, entrant ou sortant du nœud. L'intensité d'un courant (exprimée en ampères) est une grandeur algébrique (positive, négative ou nulle) définie par-rapport à l'orientation du fil. Par exemple, si l'intensité d'un courant dans un fil entrant est 3 A, cela signifie que ce fil porte un courant sortant de - 3 A.

D'après la loi des nœuds, on a donc : ${\displaystyle i_{1}+i_{2}=i_{3}+i_{4}\,}$ .

Cette loi découle directement de la conservation de la charge électrique, en tenant compte du fait qu'en régime stationnaire, ces charges ne peuvent pas s'accumuler à un endroit quelconque du circuit. Les charges qui arrivent à un nœud compensent celles qui en repartent. Cette loi permet la résolution d'« équations électriques » grâce à la méthode des nœuds[2].

Schéma d'un montage électrique illustrant la loi des mailles.
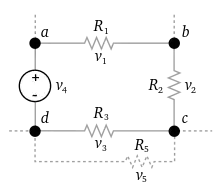
U_ab + U_bc + U_cd = U_ad ou
U_ab + U_bc + U_cd + U_da = 0
Car : U_xy = - U_yx

Dans une maille quelconque d'un réseau[3], dans l'approximation des régimes quasi stationnaires et à condition que les variations de flux magnétique à travers la maille soient négligeables, la somme algébrique des différences de potentiel le long de la maille est constamment nulle[1].

Cette loi découle de l'additivité des différences de potentiel entre deux points. La différence de potentiels entre a et b, aussi appelée tension, est exprimée par l'équation suivante : U_ab = V_a - V_b
V_a et V_b étant les potentiels respectifs aux points a et b. En additionnant toutes ces différences sur une maille fermée on obtient un résultat nul, comme illustré à gauche[2].

Cette loi permet la résolution d'« équations électriques » grâce à la méthode des mailles.

La loi des nœuds n'est valide que si le flux du champ électrique entourant chaque nœud reste nul ou constant. Elle n'est pas toujours valable en électrostatique.

Dans un semi-conducteur deux types de charges mobiles coexistent, les électrons et les trous. Le courant total, somme du courant d'électrons et du courant de trous, obéit strictement à la loi des nœuds. Pour décrire avec une excellente approximation le comportement d'un transistor bipolaire, on peut se limiter au transport d'un seul type de charge : les porteurs minoritaires dans la base. L'équation des nœuds pour ces seuls porteurs doit prendre en compte leur stockage ainsi que leur disparition par recombinaison. Cette équation, abusivement appelée équation de Kirchhoff, est améliorée pour décrire les transistors-laser est à l'origine d'un buzz médiatique en 2010[4].