Principe de superposition
On dit qu'un système de type entrée-sortie est linéaire ou relève du principe de superposition si:
- à la somme de deux entrées quelconques correspond la somme des deux sorties correspondantes,
- à un multiple d'une entrée quelconque correspond le même multiple de la sortie correspondante.
Dans le domaine des systèmes physiques et mécaniques, on appelle souvent l'entrée excitation et la sortie réponse.
Plus précisément, si l'on note les excitations ƒ (par référence aux forces en mécanique) et les réponses x (par référence aux mouvements générés par les forces) :
- lorsque l'on sollicite le système par une entrée (excitation) ƒ1, la réponse (déplacement) est x1 ;
- lorsque l'on sollicite le système par une entrée (excitation) ƒ2, la réponse (déplacement) est x2 ;
alors le système est dit linéaire si et seulement si
- pour λ1 et λ2 deux nombres quelconques, la réponse à l'excitation λ1ƒ1 + λ2ƒ2 est λ1x1 + λ2x2.
Cette définition mathématique résume les deux conditions évoquées au début de cet article.
Ce résultat se généralise alors à un nombre quelconque d'excitations. En d'autres termes, si on sait décomposer une excitation en une somme de fonctions simples, il sera éventuellement possible de calculer la réponse correspondante en additionnant des réponses individuelles calculables explicitement.
D'un point de vue épistémologique, le principe de superposition permet l'usage d'une démarche de type analyse et synthèse :
- analyse : on découpe un problème en sous-problèmes : principe de la « fracture » (al-jabr d'Al-Khawarizmi, 833), ou encore « diviser chacune des difficultés que j'examinerais, en autant de parcelles qu'il se pourrait, et qu'il serait requis pour les mieux résoudre » (René Descartes, Discours de la méthode, 1637) ;
- on étudie chaque sous-problème (sollicitations simples ƒ1, ƒ2, …) ;
- synthèse : le problème complexe est la somme des sous-problèmes.
En fait, les systèmes concrets possédant cette propriété sont rarissimes, pour ne pas dire inexistants. Bon nombre de systèmes peuvent être raisonnablement linéarisés, c'est-à-dire qu'on peut les considérer, en première approximation, comme linéaires
- soit en ignorant les petites non-linéarités par l'hypothèse des petites variations, voir systèmes oscillants à un degré de liberté et de manière générale grâce à la notion mathématique d'approximation linéaire,
- soit en procédant à une linéarisation optimisée dans le cas contraire.
En pratique, bien que peu de systèmes soient strictement linéaires, bon nombre de théories relevant de la physique et de la mécanique sont construites en considérant les systèmes linéaires. Les systèmes non linéaires sont étudiés par un grand nombre de chercheurs, mais la difficulté de leur étude fait qu'ils sont plus difficilement accessibles à un public plus large (ingénieurs, techniciens...)
Application aux circuits électriques
Dans le cas des circuits électriques composés exclusivement d'éléments linéaires (résistances, capacités, inductances, générateurs de tension ou de courant indépendants ou dépendants linéairement d'un courant, d'une tension, etc.), la réponse dans une branche est égale à la somme des réponses pour chaque générateur indépendant pris isolément, en désactivant tous les autres générateurs indépendants (générateurs de tension remplacés par des courts-circuits et générateurs de courant par des circuits ouverts).
- Exemple
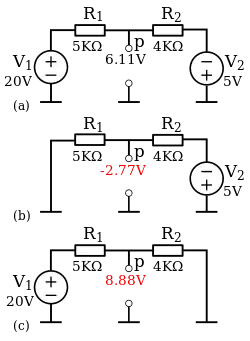
- En (a): La tension en P par rapport à la masse commune est de 6,11 volts. Cette valeur a été calculée en appliquant le principe de la superposition. Les étapes suivantes en font la démonstration.
- En (b): Court-circuit de V1 pour trouver l'influence de V2. La tension entre P et la masse devient égale à la tension aux bornes de R1. On calcule cette tension avec la formule du diviseur de tension;
- En (c): Court-circuit de V2 pour trouver l'influence de V1. La formule du diviseur de tension est de nouveau employée;
L'addition (superposition) des valeurs obtenues, nous donne bien la tension au point P de notre circuit;
- -
On peut appliquer le même principe à des circuits utilisant plus de deux sources. Aussi, chaque diviseur de tension peut comprendre un nombre quelconque de résistances en série.
Géologie
En géologie, le principe de superposition fait partie des méthodes de datation relative.
Résistance des matériaux et mécanique des milieux continus
En résistance des matériaux, on étudie des sollicitations élémentaires : traction et compression, cisaillement, torsion, flexion. Les matériaux sont d'ailleurs caractérisés par des essais mécaniques reproduisant ces sollicitations simples : essai de traction, essai de torsion, essai de flexion. À partir des charges auxquelles est soumise la pièce, on détermine les contraintes en chaque point de la pièce. Ces contraintes sont de deux types : contrainte normale, notée σ, et contrainte de cisaillement, notée τ :
- σ : traction, compression, flexion ;
- τ : cisaillement, torsion ;
la contrainte de cisaillement en flexion est en général ignorée.
Une pièce réelle est en général soumise à plusieurs sollicitations. En résistance des matériaux, on cherche à rester dans le domaine élastique, donc en petites déformations. De ce fait, on peut considérer que le système est linéaire et appliquer le principe de superposition :
- les contraintes normales s'ajoutent entre elles ;
- les contraintes de cisaillement s'ajoutent entre elles.
En particulier,
- en flexion, on établit des formulaires pour les cas simples ; pour un problème complexe, on ajoute simplement les diagrammes des efforts tranchants entre eux, les diagrammes des moments fléchissants entre eux, et les déformées entre elles ; cela revient à ajouter les contraintes ;
- dans le cas de la flexion déviée et de la flexion + traction ou compression, on ajoute les contraintes normales.
La coexistence de contraintes normale et de cisaillement (par exemple flexion + torsion) nécessite de recourir à d'autres méthodes telles que le cercle de Mohr ou la notion de contrainte équivalente.


