Contrainte de cisaillement
Une contrainte de cisaillement τ (lettre grecque « tau ») est une contrainte mécanique appliquée parallèlement à la section transversale d'un élément allongé, par opposition aux contraintes normales qui sont appliquées perpendiculairement à cette surface (donc longitudinalement, c.-à-d. selon l'axe principal de la pièce). C'est le rapport d'une force à une surface. Elle possède donc la dimension d'une pression, exprimée en pascals.
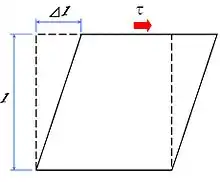
Définition
La formule générale pour calculer la contrainte de cisaillement est :
où :
- (lettre grecque « tau ») est la contrainte de cisaillement, ou « cission[1] » ;
- F est la force tangentielle appliquée ;
- A est l'aire de la section tangentielle à la force.
| Grandeur | Unités du Système international (uSI) |
Unités conventionnelles | ||
|---|---|---|---|---|
| Génie mécanique (mm kg s) | Génie mécanique (2) | Système anglo-saxon | ||
| F | newtons (N) | newtons (N) | décanewtons (daN) | livre-force (lbf) |
| A | mètre carré (m2) | millimètre carré (mm2) | centimètre carré (cm2) | pouce carré (in2) |
| pascals (Pa) | mégapascals (MPa) | bars (bar) | psi | |
Dans le cas des matériaux solides élastiques, la contrainte de cisaillement τ est reliée à la variation de l'angle droit γ par le module de cisaillement G par la relation :
L'angle γ est aussi le déplacement relatif ( sur l'image).
Le module de cisaillement est en général exprimé en mégapascals ou gigapascals. L'angle γ est toujours en radians.
Contrainte de cisaillement pour un fluide
Pour tout fluide réel possédant une viscosité, il existe des contraintes de cisaillement. En effet, même si un fluide est en mouvement, il doit avoir une vitesse nulle dans la zone de contact avec des solides. Et toute différence de vitesse au sein d'un fluide visqueux entraîne des contraintes de cisaillement : les particules fluides allant plus vite sont freinées par celles allant moins vite. C'est d'ailleurs pour cela qu'il faut exercer une certaine force pour mettre un fluide en mouvement.
La relation entre contrainte de cisaillement et gradient de vitesse s'écrit, pour un fluide newtonien :
où :
- = la viscosité dynamique ;
- = la vitesse du fluide à une hauteur ;
- = la coordonnée d'espace repérant la position du fluide.
Contraintes sur les matériaux
En théorie des poutres


Dans la théorie des poutres, donc sur les pièces élancées (plus longues que larges), le cisaillement intervient lorsque l'on a un effort tranchant : si x est l'axe de la poutre, les composantes Ty et/ou Tz du torseur de cohésion sont non nulles.
Cisaillement simple
On a du cisaillement simple lorsque l'on applique deux forces et perpendiculairement à l'axe, les points d'application étant légèrement décalées (d'une quantité notée d sur le schéma ci-contre) : s'ils sont au droit (à la même abscisse), on a du pincement, et s'ils sont très éloignés, on a de la flexion. On remarque au passage qu'il en résulte un moment de couple T×d, qui doit être compensé par ailleurs, c'est ce couple qui crée de la flexion. La longueur de d permet de différencier le cisaillement pur (cisaillement théorique dont le torseur de cohésion ne contient qu'un effort tranchant) du cisaillement simple (qui lui contient un moment de flexion)
Le cisaillement simple a lieu entre les points d'application de la force ; on n'est donc pas dans les conditions d'application du principe de Saint-Venant. On considère que la contrainte est uniforme :
où S est l'aire de la section droite.
La matière reste dans le domaine élastique tant que le cisaillement vérifie :
- τ ≤ Reg
où Reg est la limite d'élasticité au glissement. Elle est reliée aux limites d'élasticité à la traction (Re) et à la compression (Rec) par[2] :
avec
- .
Typiquement :
- pour les aciers doux (Re ≤ 270 MPa) et les alliages d'aluminium : Reg = 0,5×Re ;
- pour les aciers mi-durs (320 ≤ Re ≤ 500 MPa) : Reg = 0,7×Re ;
- pour les aciers durs (Re ≥ 600 MPa) et les fontes : Reg = 0,8×Re.
Pour valider une conception, on applique en général un coefficient de sécurité s. La validation à l'état limite ultime (ELU) s'exprime alors par la condition
- τ ≤ Rpg
où Rpg est la résistance pratique au glissement, Rpg = Reg/s.
Cas de la flexion
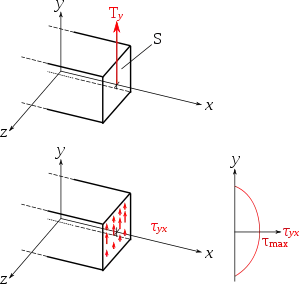
Dans le cas de la flexion (d « suffisamment grand »), la contrainte n'est plus uniforme : dans les conditions du principe de Saint-Venant (donc loin des points d'application des forces), les conditions d'équilibre imposent que la contrainte sur une surface libre soit perpendiculaire à cette surface, donc τ = 0 en haut et en bas, et elle est maximale sur la fibre neutre. Cette remarque a d'abord été formulée par l'ingénieur russe des chemins de fer D. Jouravski, chargé du franchissement de la Verevia. Il y établit l'un des plus grands ouvrages de la ligne Nicolaïev : un pont en treillis Howe en charpente, comportant 9 travées, une portée totale de 60 m et des piles hautes de 55 m. Mais si le bois est naturellement résistant en compression dans le sens des fibres, il est beaucoup plus vulnérable au cisaillement : Jouravski s'avisa qu'il fallait apprécier ce type d'effort précisément ; or la littérature scientifique de l'époque était encore quasiment muette sur la répartition de ce type de contrainte[3].
Dans la théorie d'Euler-Bernoulli, le cisaillement est négligé pour la flexion. Il est par contre pris en compte dans la théorie de Timoshenko (pour les poutres épaisses).
Cas de la torsion
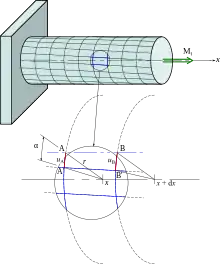
Au cours d'une torsion, la matière est soumise à du cisaillement pur.
Dans le cas d'une pièce de section cylindrique fermée, il s'agit de torsion uniforme. La contrainte est nulle au centre (à la fibre neutre) et est maximale en périphérie. Cette contrainte maximale peut être calculée par :
où
- Mt est le moment de torsion ;
- C est le module de torsion, dépendant de la géométrie de la section.
Cependant, pour les sections creuses (de formes convexes), la contrainte tangente s'exprime en fonction de l'épaisseur (t) comme suivant:
tel que est l'aire du contour tracé à mi-épaisseur de la paroi.
En théorie des plaques

En théorie des plaques, lorsque l'on isole un élément de plaque, il faut définir le cisaillement sur deux paires de faces opposées. Si l'axe z est normal à la plaque, on appelle qx l'effort tranchant sur la face normale à l'axe x, et qy l'effort tranchant sur la face normale à l'axe y. Dans une situation de flexion, la répartition des cissions τxz(z ) et τyz(z ) est identique au cas de la poutre en flexion.
Exemple d'applications
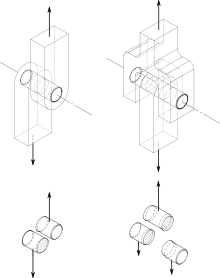
En génie mécanique, les cas de rupture en cisaillement concernent essentiellement les axes. Le point primordial consiste à dénombrer les sections cisaillées.
Dans le cas d'une articulation en porte-à-faux (cas typique d'une paumelle), il n'y a qu'une seule section cisaillée. Si l'axe a un diamètre d, l'aire cisaillée vaut simplement
- S = πd2/4.
Dans le cas d'une articulation en chape, il faut que la pièce se rompe en deux endroits, il y a donc deux sections cisaillées. L'aire cisaillée vaut donc
- S = 2×πd2/4.
Axe d’articulation
La force N soumet l’axe à un cisaillement selon deux sections S déterminées par l’assemblage tirant et chape (fig. 1).
La contrainte de cisaillement sera : ,
soit : .
Assemblage par rivet et boulon
Les assemblages rivetés et boulonnés sont des assemblages par adhérence. C'est l'adhérence qui s'oppose aux efforts, si la conception est correcte il ne devrait jamais y avoir de cisaillement. Si toutefois il n'était pas possible d'exercer un effort presseur suffisant (cas des vis à bois par exemple), il faut dimensionner au cisaillement.
Dans le cas d’un cisaillement pur, la formule s’applique pour chaque section (la fig. 3 a deux sections, les fig. 2 et 4 ont quatre sections soumises au cisaillement).
Contrainte sur filets de vis
À la figure 5, la force tangentielle maximale (force de serrage) appliquée à la tige de la vis sera égale au produit de la section annuaire (périmètre à fond de filet par la hauteur utile de l’écrou) par la valeur de la résistance au cisaillement de la matière.
Composantes du tenseur des contraintes
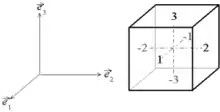
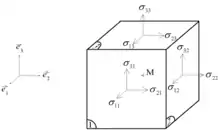
Un solide est décrit dans un repère orthonormé direct. Considérons un cube de matière de côté a dont les faces sont normales aux axes du repère. Numérotons ses faces :
- les faces i et -i sont les faces normales à , en partant du centre du cube, pointe vers i, la face -i étant la face opposée.
Sur la face 1 s'exerce un vecteur-force . La composante tangentielle de cette force crée un cisaillement. Si le vecteur force a pour composantes
alors le vecteur tangentiel a pour composantes
on définit donc, pour la face 1, deux composantes de la contrainte de cisaillement :
- σ21 = F21/a2
- σ31 = F31/a2
De manière générale, pour la face j, on définit les deux cissions σij, i ≠ j. Ces contraintes sont des composantes du tenseur des contraintes. On les note parfois τij, i ≠ j.

Si l'élément de matière est à l'équilibre, il ne doit pas se déplacer. La contrainte qui s'exerce sur la face -j est donc l'opposée de celle qui s'exerce sur j : σi -j = -σij : elles sont symétriques.
Par ailleurs, ces contraintes créent un couple. Or, à l'équilibre, l'élément de matière ne doit pas tourner, on a donc un couple opposé (σji, σj -i). On en déduit que le tenseur des contraintes est symétrique :
- σji = σij.
Cercle de Mohr

Dans le cas du cisaillement pur, le cercle de Mohr est centré sur l'origine du repère.
Voir aussi
Notes et références
- Ce néologisme a été introduit par les auteurs du « Dictionnaire français de rhéologie » (1988), qui rechignaient à utiliser le terme (correct) de « scission. »
- D. Spenlé et R. Gourhant, Guide du calcul en mécanique : maîtriser la performance des systèmes industriels, Paris, Hachette, , 272 p. (ISBN 2-01-168835-3, BNF 39021238), p. 191
- D'après Timoshenko, History of strength of materials, McGraw-Hill Book Co., (réimpr. 1983, éd. Dover), 452 p., « Strength of Materials between 1833 and 1867 », p. 142.























