Valeur propre (synthèse)
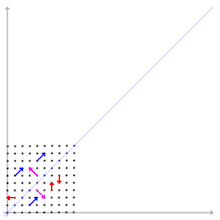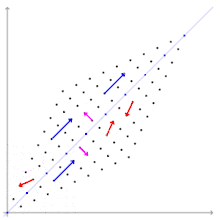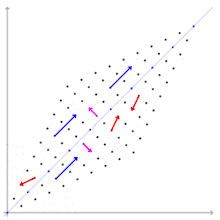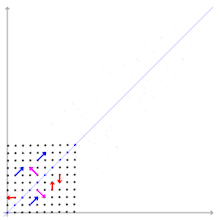
Les notions de vecteur propre, de valeur propre, et de sous-espace propre s'appliquent à des endomorphismes (ou opérateurs linéaires), c'est-à-dire des applications linéaires d'un espace vectoriel dans lui-même. Elles sont intimement liées, et forment un pilier de la réduction des endomorphismes, partie de l'algèbre linéaire qui vise à décomposer de la manière la plus efficace possible l'espace en somme directe de sous-espaces stables.
Définitions et propriétés
Dans toute la suite, on considère un espace vectoriel E, sur un corps commutatif K. Les éléments de E sont les vecteurs et ceux de K sont les scalaires. En pratique, le corps K est souvent le corps ℂ des complexes et l'espace vectoriel est de dimension finie. On précisera dans chaque section, les restrictions éventuelles sur le corps ou la dimension. On notera u un endomorphisme de E et Id l'endomorphisme identité.
Valeur propre
Définition — Un scalaire λ est une valeur propre de u s'il existe un vecteur x non nul tel que u(x) = λx.
Les valeurs propres de u sont donc les scalaires λ tels que u – λId n'est pas injectif (autrement dit son noyau n'est pas réduit au vecteur nul).
Les valeurs propres d'une matrice carrée A de taille n sont les valeurs propres de l'endomorphisme de Kn de matrice A dans la base canonique.
Si E est de dimension finie n, les valeurs propres de u (ou de sa matrice A dans n'importe quelle base) :
- sont les racines de leur polynôme caractéristique commun, det(XId – u) = det(XIn – A) ;
- sont toutes les valeurs spectrales de u (ou de A) : les éléments de leur spectre commun.
Exemples :
- si u = Id alors u ne possède qu'une valeur propre : 1.
- si u est défini sur ℝ2 par alors u possède deux valeurs propres :
- 4 car
- –1 car
- pas d'autre valeur propre puisque la dimension est 2.
Vecteur propre
Définition — Soit x un vecteur non nul de E, x est un vecteur propre de u s'il existe un scalaire λ tel que u(x) = λx. On dit que x est un vecteur propre associé à la valeur propre λ.
Les vecteurs propres (associés à une valeur propre λ) d'une matrice carrée A de taille n sont les vecteurs propres (associés à la valeur propre λ) de l'endomorphisme de Kn représenté par A.
- Un vecteur propre ne peut pas être associé à deux valeurs propres différentes
- Une famille de k vecteurs propres associés à k valeurs propres différentes constitue une famille libre.
Sous-espaces propres
Définition — Soit λ une valeur propre de u (resp. A) ; alors l'ensemble constitué des vecteurs propres pour la valeur propre λ et du vecteur nul est appelé le sous-espace propre de u (resp. A) associé à la valeur propre λ.
- Le sous-espace propre associé à une valeur propre λ est le noyau de u – λId. C'est donc un sous-espace vectoriel.
- Par définition d'une valeur propre, un sous-espace propre n'est jamais réduit au vecteur nul.
- Pour une matrice carrée A de taille n, on trouve le sous-espace propre associé à une valeur propre λ en résolvant le système (homogène) de n équations linéaires à n inconnues dont l'écriture matricielle est (A – λIn)v = 0.
- Les espaces propres Ei de valeurs propres λi forment une somme directe de sous-espaces vectoriels stables par u.
C'est une conséquence du lemme des noyaux, appliqué aux polynômes X – λi, qui sont deux à deux premiers entre eux.
Cette somme directe des Ei est égale à E si et seulement si l'endomorphisme est diagonalisable. - Si deux endomorphismes u et v commutent, alors tout sous-espace propre de u est stable par v.
Polynôme caractéristique
On suppose ici que E est de dimension finie n.
On appelle « polynôme caractéristique » de l'endomorphisme u, le polynôme det(XId – u), et « polynôme caractéristique » d'une matrice carrée A d'ordre n, le polynôme caractéristique de l'endomorphisme de Kn canoniquement associé à A, c'est-à-dire le polynôme det(XIn – A), où In est la matrice identité n×n. Ce polynôme est de degré n, donc a au plus n racines.
- Soit a : E → F un isomorphisme d'espaces vectoriels, c'est-à-dire une application linéaire bijective, alors u et aua−1 ont même polynôme caractéristique et donc mêmes valeurs propres.
En effet, - Le polynôme caractéristique de u est donc égal à celui de sa matrice A dans n'importe quelle base.
- Les racines du polynôme caractéristique de u (ou de A) sont ses valeurs propres.
En effet, un endomorphisme est de déterminant nul si et seulement s'il est non injectif. - Si K est algébriquement clos, ou encore si K est R le corps des nombres réels et n est impaire, alors u possède au moins une valeur propre.
Dire qu'un corps est algébriquement clos, c'est dire que tout polynôme non constant admet au moins une racine. Cette racine est nécessairement une valeur propre, d'après le premier point ci-dessus. D'autre part, un polynôme réel de degré impair a toujours une racine réelle.
L'ordre de multiplicité algébrique d'une valeur propre λ est l'ordre de multiplicité de la racine dans le polynôme caractéristique. C'est donc l'exposant de (X – λ) dans le polynôme caractéristique.
- Dans un corps algébriquement clos :
- Le déterminant est égal au produit des valeurs propres élevées à leur ordre de multiplicité algébrique ;
- La trace est égale à la somme des valeurs propres multipliées par leur ordre de multiplicité algébrique.
Polynôme minimal
On se place ici dans le cadre d'un espace vectoriel E de dimension finie.
On appelle « polynôme minimal » de u le polynôme unitaire de plus petit degré qui annule u. Le polynôme minimal donne une relation de dépendance linéaire sur les puissances u0, u1, u2, …, de l'endomorphisme, et réciproquement une telle relation de dépendance linéaire fournit un polynôme annulateur de u, le polynôme minimal en minimisant le degré et en prenant le coefficient 1 pour la plus grande puissance de u qui intervient.
- Les racines du polynôme minimal sont les valeurs propres de u.
- Si le polynôme minimal se factorise M = (X – λ)Q, alors M(u) = (u – λId)∘Q(u) est l'endomorphisme nul, alors que Q(u) ne l'est pas (car le degré de Q est trop bas). Par conséquent il existe des vecteurs non nuls dans l'image de Q(u), qui sont des vecteurs propres pour λ.
- Plus généralement pour tout entier i ≥ 1, le polynôme minimal est divisible par (X – λ)i si et seulement si le noyau de (u – λId)i est strictement plus grand que celui de (u – λId)i–1. Par conséquent, la multiplicité m de λ comme racine du polynôme minimal est égale au plus petit exposant tel que le noyau de (u – λId)m soit égal au sous-espace caractéristique associé à la valeur propre λ. On l’appelle multiplicité minimale de λ.
- Soit a un automorphisme de E, alors u et aua−1 ont même polynôme minimal (et donc mêmes valeurs propres). Autrement dit le polynôme minimal est un invariant de similitude de l'endomorphisme.
En effet, P(aua−1) est égal à aP(u)a−1, pour tout polynôme P. - Sur un corps algébriquement clos, le polynôme minimal (comme tout polynôme non nul) est scindé, et possède donc au moins une racine, qui est valeur propre de u (exception : si la dimension de E est nulle, le polynôme minimal est 1, tout comme le polynôme caractéristique, et u n'a pas de valeur propre).
- Le théorème de Cayley-Hamilton permet d'affirmer que le polynôme minimal divise le polynôme caractéristique
Sous-espaces caractéristiques
On suppose que E est de dimension finie et que K est algébriquement clos.
Si λ est une valeur propre de u, dont l'ordre de multiplicité est αλ, on appelle « sous-espace caractéristique » de u associé à la valeur propre λ le noyau de (u – λId)αλ. On notera ce sous-espace caractéristique Eλ.
- Eλ est aussi le noyau de (u – λId)βλ où βλ est l'ordre de multiplicité de λ dans le polynôme minimal.
- Eλ est stable par u.
- dim(Eλ) = αλ.
- L'espace E est somme directe de ses sous-espaces caractéristiques.
- la restriction de u à Eλ a pour polynôme minimal (X – λ)βλ.
Réduction d'endomorphisme
On suppose que E est de dimension finie. L'étude des valeurs propres permet de trouver une forme plus simple des endomorphismes, c'est ce qu'on appelle leur réduction.
Diagonalisation
L'endomorphisme est entièrement déterminé par ses vecteurs propres et ses valeurs propres associées s'il est diagonalisable, c'est-à-dire s'il existe une base de vecteurs propres. Des exemples numériques sont donnés dans l'article « Matrice diagonalisable ». Les critères suivants sont tous des conditions nécessaires et suffisantes pour qu'un endomorphisme d'un espace vectoriel de dimension finie soit diagonalisable :
- Il existe une base de vecteurs propres
- la somme des espaces propres est l'espace entier
- la somme des dimensions des espaces propres est égale à la dimension de l'espace entier
- le polynôme minimal est scindé sur K et à racines simples. (Démonstration dans Polynôme d'endomorphisme.)
- tout sous-espace propre possède une dimension égale à la multiplicité algébrique de la valeur propre associée.
- toute représentation matricielle M de u est diagonalisable, c'est-à-dire peut s'écrire sous la forme M = PDP−1 avec P et D matrices respectivement inversible et diagonale.
À ces propriétés équivalentes s'ajoutent les implications suivantes :
- S'il existe dim(E) valeurs propres distinctes, alors u est diagonalisable.
- Si u est diagonalisable, alors son polynôme caractéristique est scindé.
Dans le cas où le corps est ℂ, cette propriété est presque partout vraie au sens de la mesure de Lebesgue. De plus, dans l'espace topologique des endomorphismes de E, le sous-ensemble de ceux qui sont diagonalisables est alors dense.
Décomposition de Dunford
Si le polynôme minimal de u est scindé, alors u peut s'écrire sous la forme u = d + n avec d diagonalisable et n nilpotent tels que dn = nd. De plus, d et n sont des polynômes en u.
Représentation de Jordan
On suppose que K est algébriquement clos.
La représentation de Jordan prouve qu'alors, tout endomorphisme u de E est trigonalisable. Elle démontre que la restriction de u au sous-espace caractéristique associé à la valeur propre λ possède une représentation formée de blocs de la forme
appelés « blocs de Jordan » et que l'endomorphisme possède une représentation matricielle sous la forme
où les scalaires λi (non nécessairement distincts) sont les valeurs propres de u.
Voir aussi
Articles connexes
Bibliographie
- Serge Lang, Algèbre [détail des éditions]
- Haïm Brezis, Analyse fonctionnelle : théorie et applications [détail des éditions]
- Walter Rudin, Analyse fonctionnelle [détail des éditions]
- (en) Nelson Dunford et Jacob T. Schwartz, Linear Operators, Part I General Theory, Wiley-Interscience, 1988








