Espace à quatre dimensions

Se repérer dans un plan demande d'y définir deux axes, et passer du plan à l'espace revient de ce point de vue à ajouter un troisième axe sortant du plan. En partant des repères familiers de l'espace usuel (souvent matérialisés par les arêtes joignant deux murs et le plancher d'une pièce), l'idée d'un quatrième axe perpendiculaire aux trois premiers (impossible dans notre espace) permet d'imaginer — par exemple en pensant à des représentations en perspective — un système à quatre coordonnées, et des déplacements dans huit directions principales : avant et arrière, gauche et droite, haut et bas[n 7], et deux nouvelles directions pour lesquelles le vulgarisateur Hinton a inventé les termes ana et kata, à partir de préfixes grecs signifiant respectivement « vers le haut » et « vers le bas »; ces nouvelles directions sont perpendiculaires à toutes les directions de l'espace tridimensionnel familier. Les axes de cet espace étant généralement notés x, y et z, le nouvel axe est alors noté w (et non t, puisqu'on ne parle plus du temps, mais d'une nouvelle dimension spatiale), les coordonnées (longueur, largeur et hauteur, ou plus techniquement abscisse, ordonnée et cote) se voyant adjoindre un nouveau terme, la spissitude, reprenant une idée de Henry More[4].

Quand un objet tridimensionnel traverse un plan, les habitants de ce plan le perçoivent sous forme de sections. Par exemple, si une sphère traverse un plan, les observateurs bidimensionnels verront apparaître un point, puis un cercle grandissant jusqu'au diamètre de la sphère, et rétrécissant ensuite jusqu'à disparaître. Par analogie, une hypersphère traversant notre espace devrait apparaître comme une sphère gonflant, puis diminuant avant de disparaître[24]. Cette méthode de visualisation d'objets à quatre dimensions est utilisée dans plusieurs ouvrages de Charles Howard Hinton[13]^:11-14.

Une autre méthode de visualisation consiste à étudier des projections. Les représentations d'objets en trois dimensions sur une surface plane utilisent généralement des transformations géométriques, dont les plus élaborées (les transformations projectives[n 8]) proviennent à l'origine des travaux des peintres du Quattrocento, inventant les lois de la perspective[26] ; la troisième dimension (la profondeur) est souvent, dans ce cas, donnée par des indices indirects, tels que les ombres, les reflets ou le flou de l'éloignement[27]. Ces projections déforment les objets, les faces carrées d'un cube devenant des parallélogrammes[28].

De façon analogue, des objets de la quatrième dimension peuvent être projetés sur notre espace ; avec de l'entraînement, on peut attribuer les déformations correspondantes à la spissitude (la « profondeur » dans la quatrième dimension)[n 9].

Les images ci-dessous illustrent ce principe, montrant trois projections d'un tesseract (l'analogue du cube à quatre dimensions), déterminées par analogie avec les projections correspondantes d'un cube ; le calcul rigoureux montre qu'il s'agit bien des véritables projections (au sens mathématique).

Cube	Tesseract	Description
		Le cube vu de face (il s'agit d'une projection orthogonale). La projection analogue d'un tesseract est un cube, identifiable à la « face » avant du tesseract (plus rigoureusement, à sa 3-face, encore appelée cellule). Les sept autres cellules sont invisibles, cachées comme les cinq autres faces du cube.
		La projection est faite perpendiculairement à une arête (dans le cas du cube) et donc à une face (un carré) dans le cas du tesseract. Pour donner un sens de la profondeur, la projection est à présent une perspective à point de fuite : les arêtes supérieures et inférieures des faces du cube, parallèles dans la réalité, se coupent à présent (sur l'horizon). On observe sur la projection du cube deux trapèzes accolés ; la projection du tesseract est donc formée de deux troncs de pyramide.
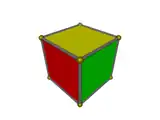
		Le cube vu par la pointe (l'axe de perspective est une grande diagonale du cube) : les faces carrées visibles deviennent trois losanges déformés autour du sommet. L'analogue pour le tesseract est formé de quatre volumes hexaédriques (des parallélépipèdes déformés) entourant le sommet (situé au centre du volume image). Les quatre autres cellules restent cachées.

Ombre d'un tesseract.

Une illustration du traité de Jouffret[15].

Une variante consiste à interpréter plus physiquement ces projections comme correspondant à l'ombre portée d'un objet : puisque l'ombre sur un plan d'un cube (matérialisé par ses arêtes) est formée de deux carrés dont les sommets sont reliés entre eux, l'analogie prédit que l'ombre d'un tesseract sera un cube suspendu à l'intérieur d'un autre cube, comme on le voit sur la figure de gauche[n 9].

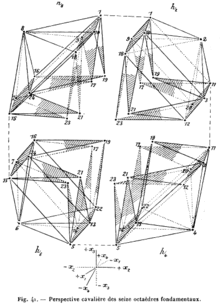
Les techniques de la géométrie descriptive, représentant le même objet par trois projections orthogonales, peuvent là aussi permettre, par analogie, des représentations (par quatre projections) d'objets en 4D, comme sur l'illustration de droite, représentant une des cellules octaédriques du 24-cellules[29].

Patron d'un cube et son pliage.

Patron d'un tesseract et son pliage.

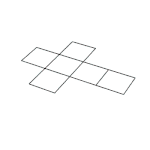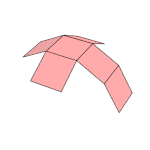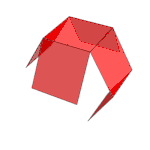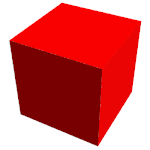
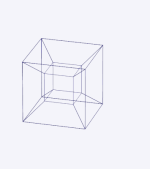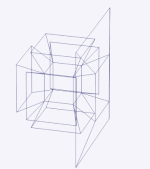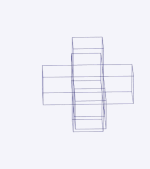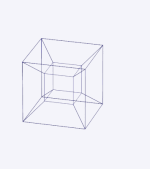
On peut (figure de gauche) tracer dans un plan le patron d'un cube et donner des indications de repliage (évidemment inutilisables pour un habitant du plan) permettant de construire le cube lui-même. La figure animée de droite tente de montrer de même comment replier le patron d'un tesseract[30].

Bien que considérer le temps comme une quatrième dimension ne permette pas le plus souvent d'en percevoir les propriétés géométriques[18], certaines configurations simples peuvent être plus aisément visualisées en les interprétant de manière cinématique. Par exemple, une droite de l'espace usuel se déplaçant dans un mouvement de translation uniforme décrit un plan de l'espace-temps ; on voit alors que l'intersection de deux plans correspond aux points de l'espace-temps où les deux droites se coupent, ce qui se produira en général en un lieu et un temps uniques, et donc que l'intersection de deux plans en 4D est en général réduite à un point[31].

Ces différentes méthodes sont utiles en première approche, mais elles souffrent de plusieurs limites : elles ne permettent pas de soupçonner l'existence d'objets sans analogue tridimensionnel, comme le sixième polytope régulier, ni de prédire la plupart des résultats quantitatifs, comme le volume de l'hypersphère, lequel n'est pas ${\displaystyle 6\pi r^{3}}$ (ou peut-être ${\displaystyle 8\pi r^{3}}$), comme on pourrait le penser en prolongeant la série ${\displaystyle 2\pi r}$ (pour le périmètre d'un cercle) et ${\displaystyle 4\pi r^{2}}$ (pour l'aire d'une sphère), mais est donné par la formule inattendue ${\displaystyle V_{3}=2\pi ^{2}r^{3}}$[n 10]. Enfin, elles peuvent amener à des erreurs importantes : ainsi, les rotations du plan se faisant autour d'un point fixe, et celles de l'espace autour d'un axe fixe, on pourrait croire que les rotations 4D se font autour d'un plan fixe, mais ce n'est le cas que pour des rotations très particulières[32].

Une construction axiomatique selon la méthode des Éléments (ou d'une version plus moderne et plus rigoureuse, telle que celle de Hilbert) est possible et a été proposée par Grassmann dès 1840, formalisée par Cayley et Sylvester, et vulgarisée par exemple par Schubert en 1905[34] ; outre les points, droites et plans familiers, on définit un nouvel objet primitif, l'hyperplan[n 11], et une série de nouveaux axiomes : la géométrie d'un hyperplan est la géométrie de l'espace usuel à trois dimensions, par quatre points non coplanaires passe un hyperplan et un seul[n 12], par tout point d'un hyperplan passe une droite perpendiculaire à toutes les droites de cet hyperplan passant par ce point[n 13], etc.

Une approche plus moderne utilisant cependant le même vocabulaire, comme celle proposée par Jouffret[15], définit l'espace à quatre dimensions comme étant simplement ${\displaystyle \mathbb {R} ^{4}}$ (c’est-à-dire que chaque point est identifié à une suite de quatre nombres, ses coordonnées), mais traduit ensuite les ensembles et les équations dans le langage de la géométrie classique, définissant par exemple un plan comme la donnée d'un système de deux équations à quatre inconnues, représentant les quatre coordonnées des points du plan[35].

La géométrie ainsi construite est euclidienne (au sens où, par exemple, la somme des angles d'un triangle reste égale à 180°) ; ce ne fut pas toujours bien compris par les contemporains, car l'apparition presque simultanée des géométries non euclidiennes avait amené à des confusions mettant dans le même ensemble de mathématiques exotiques, voire pathologiques, toutes ces idées incompatibles avec l'intuition géométrique usuelle[36].

Beaucoup d'objets d'étude de la géométrie dans l'espace (droites et plans, distances et angles, polyèdres, surfaces classiques comme les sphères ou les tores, déplacements, etc.) se généralisent ou ont des analogues à quatre dimensions, mais certaines propriétés de ces nouveaux objets sont assez différentes ou plus complexes, en raison d'un nombre plus grand de degrés de liberté.

Intersection de deux plans dans un espace à quatre dimensions. La quatrième dimension est représentée par la couleur, de 0 (blanc) à 1 (noir) ; ainsi B et C (respectivement dans les plans α et β) sont distincts. L'intersection des plans est le point origine des coordonnées.

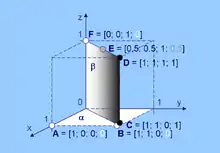
La position relative de deux plans est une bonne illustration de la complexité apportée par la quatrième dimension : contrairement à ce qui se passe dans l'espace usuel (où deux plans distincts ne peuvent être que parallèles ou avoir une droite en commun), deux plans n'ont en général qu'un seul point en commun, mais ils peuvent (s'ils sont contenus dans le même hyperplan) avoir une droite en commun, et deux types de « parallélisme » (c'est-à-dire de non intersection) sont possibles : les deux plans peuvent être parallèles à une même droite (chaque plan définissant avec la droite un hyperplan, les deux hyperplans étant distincts), ou les deux plans peuvent être complètement parallèles, c'est-à-dire parallèles dans le même hyperplan[37] - [31].

Bien que les méthodes classiques de la géométrie euclidienne suffisent pour démontrer ce genre de résultat, les démonstrations et les calculs sont bien plus aisés à l'aide des outils de l'algèbre linéaire, et analyser tous les cas de figure possibles d'une situation plus complexe, telle que la configuration de quatre hyperplans, relèverait même plutôt des méthodes de la géométrie énumérative.

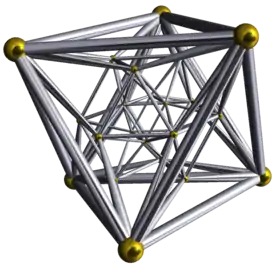
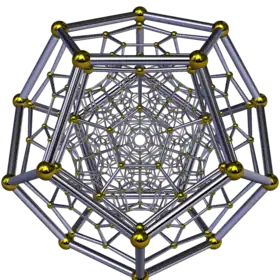
Les cinq polyèdres réguliers (connus sous le nom de solides de Platon) ont pour analogue des 4-polytopes (appelés polychores réguliers), dont les « faces » (ou plutôt les 3-faces, ou cellules) sont des polyèdres réguliers ; il en existe six, représentés ci-dessous ; cinq ont des relations étroites avec les cinq solides de Platon, mais le sixième, l'icositétrachore, ou 24-cellules, ne pourrait se deviner par simple analogie. En affaiblissant les conditions de régularité, on obtient dans l'espace usuel 13 polyèdres semi-réguliers, les solides d'Archimède ; en dimension 4, il existe de même une soixantaine de 4-polytopes uniformes, dont beaucoup n'ont aucun analogue tridimensionnel[38].

Les 6 polychores réguliers et leurs diagrammes de Schlegel.

Nom du polychore	Pentachore (hypertétraèdre)	Tesseract (hypercube)	Hexadécachore (hyperoctaèdre)	Icositétrachore (24-cellules)	Hécatonicosachore (hyperdodécaèdre)	Hexacosichore (hypericosaèdre)
Image
Projeté dans un	Tétraèdre	Cube	Tétraèdre	Octaèdre	Dodécaèdre	Icosaèdre
Diagramme correspondant

La 3-sphère en rotation, projetée dans notre espace.

Ces objets généralisent les objets correspondants de l'espace ; il s'agit d'ensembles paramétrés (de manière régulière) par un, deux ou trois paramètres (autrement dit, on peut s'y déplacer suivant un, deux ou trois degrés de liberté). La description la plus générale de ces ensembles a été construite par Bernhard Riemann (dans sa thèse de 1854[n 5]) sous le nom de variétés, ici plongées dans l'espace à quatre dimensions.

L’ensemble des points situés à la même distance R d’un point fixé P₀ est une hypersurface, la 3-sphère (de centre P₀ et de rayon R), souvent appelée hypersphère lorsque la dimension est claire d'après le contexte. On peut repérer les points de la 3-sphère à l'aide des coordonnées hypersphériques, définies de manière analogue aux coordonnées sphériques. Son volume est ${\displaystyle V_{3}=2\pi ^{2}R^{3}}$ et le domaine qu'elle délimite a pour hypervolume ${\displaystyle V_{4}={\begin{matrix}{\frac {1}{2}}\end{matrix}}\pi ^{2}R^{4}}$, mais ces formules ne peuvent en revanche pas être obtenues par analogie, et demandent les outils du calcul intégral[n 10]. L'hypersphère est la plus simple des 3-variétés de courbure non nulle et a servi de modèle cosmologique à l'univers décrit par la relativité générale[39].

Dans l'espace usuel, un cylindre peut être interprété comme le résultat du déplacement d'un cercle dans une direction hors de son plan, ou, plus abstraitement, comme le produit cartésien d'un cercle par une droite. En quatre dimensions, plusieurs objets distincts généralisent ces définitions : déplaçant une sphère hors de son hyperespace, on obtient une hypersurface, appelée cylindre sphérique ; déplaçant de même un cylindre (ou, ce qui revient au même, déplaçant un cercle dans deux directions), on obtient une autre hypersurface, le cylindre cubique. Enfin, le produit cartésien de deux cercles, dont le tore de Clifford est un plongement dans la 3-sphère, est une surface topologiquement semblable à un tore, mais qui n'a pas de courbure. Suivant les auteurs, ces différents termes désignent parfois non des surfaces ou des hypersurfaces, mais des sous-ensembles de l'espace bornés par elles ; par exemple, le cylindre sphérique désigne parfois le produit d'une boule par un segment de droite, et le double cylindre la région de la 3-sphère bornée par le tore de Clifford (une portion d'hypersurface), ou même le produit de deux disques[40].

La classification des surfaces fermées de l'espace usuel (au sens topologique, qui veut qu'une tasse de café soit indiscernable d'un beignet pour un mathématicien[41]) a été achevée par Poincaré en 1907 ; le résultat correspondant pour les hypersurfaces de l'espace à quatre dimensions (dont un cas particulier est la conjecture de Poincaré) est la conjecture de géométrisation de Thurston, qui ne fut formulée par lui qu'en 1976 et démontrée par Perelman en 2003 ; cette classification est complexe et pratiquement impossible à visualiser ou même à vulgariser[42].

Dans l'espace usuel, une courbe fermée peut former un nœud, mais une surface (semblable à une sphère) ne le peut pas[n 14]. En quatre dimensions, la situation s'inverse : une courbe qui semble nouée peut se ramener à un cercle en déplaçant les croisements apparents dans la quatrième direction, mais au contraire on peut fabriquer des surfaces nouées homéomorphes à une sphère, par exemple en partant d'un nœud simple de l'espace usuel et en le faisant tourner autour d'un plan bien choisi. La théorie de ces nœuds est là aussi beaucoup plus complexe que la théorie des nœuds usuelle[43].

Résoudre des questions de ce genre, et même simplement les formuler rigoureusement, demande l'utilisation d'outils plus abstraits que ceux de la géométrie classique : topologie combinatoire, homotopie, géométrie algébrique, etc.

Comme en dimension trois, les déplacements 4D sont des composées de translations et de rotations ; ces dernières (définies comme des isométries directes ayant un point fixe) n'ont en général qu'un seul point fixe et sont composées de rotations autour de deux plans orthogonaux invariants. Lorsque ces deux rotations ont le même angle, il existe toute une famille de plans invariants et dans lesquels la rotation se fait selon le même angle ; on parle alors de rotation isocline[32]. L'étude de ces transformations relève plutôt de l'algèbre linéaire et du calcul matriciel, plus précisément de la technique de réduction des endomorphismes (utilisant en particulier les notions de vecteur propre et de sous-espace caractéristique).

Formellement, l’espace à quatre dimensions est défini comme un espace affine euclidien (de dimension 4)[44].

La représentation algébrique la plus simple de cet espace consiste à identifier chaque point au vecteur de ses quatre coordonnées dans un repère orthonormal, l'espace vectoriel correspondant étant identifié à ${\displaystyle \mathbb {R} ^{4}}$ ; le vecteur ${\displaystyle \mathbf {a} }$ s'écrit alors ${\displaystyle \mathbf {a} =(a_{1},a_{2},a_{3},a_{4}).}$ Les quatre vecteurs de la base canonique (e₁, e₂, e₃, e₄) sont donnés par ${\displaystyle \mathbf {e} _{1}=(1,0,0,0)\$ ;\mathbf {e} _{2}=(0,1,0,0)\ ;\mathbf {e} _{3}=(0,0,1,0)\ ;\mathbf {e} _{4}=(0,0,0,1),} et le vecteur général s'écrit donc ${\displaystyle \mathbf {a} =a_{1}\mathbf {e} _{1}+a_{2}\mathbf {e} _{2}+a_{3}\mathbf {e} _{3}+a_{4}\mathbf {e} _{4}.}$

Les calculs vectoriels se font comme dans l'espace usuel ${\displaystyle \mathbb {R} ^{3}}$, le produit scalaire se généralise de même à

${\displaystyle \mathbf {a} \cdot \mathbf {b} =a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}+a_{4}b_{4}}$

et permet de calculer la norme (donc la distance entre deux points) par la formule (généralisant le théorème de Pythagore)

${\displaystyle \left|\mathbf {a} \right|={\sqrt {\mathbf {a} \cdot \mathbf {a} }}={\sqrt {a_{1}^{2}+a_{2}^{2}+a_{3}^{2}+a_{4}^{2}}},}$

et de définir l'angle ${\displaystyle \theta }$ entre deux vecteurs non nuls par ${\displaystyle \theta =\arccos {\frac {\mathbf {a} \cdot \mathbf {b} }{\left|\mathbf {a} \right|\left|\mathbf {b} \right|}}}$[44]. Il n'existe en revanche pas de produit vectoriel en 4 dimensions[n 15].

Cette représentation permet d'utiliser les outils de la géométrie analytique, en ramenant les objets à étudier à leurs équations cartésiennes. Par exemple, un hyperplan est formé de tous les points de coordonnées ${\displaystyle (x,y,z,w)}$ vérifiant une équation de la forme ${\displaystyle ax+by+cz+dw=e}$ et il est orthogonal aux droites de vecteur directeur ${\displaystyle (a,b,c,d)}$ ; l'hypersphère de centre ${\displaystyle P_{0}=(x_{0},y_{0},z_{0},w_{0})}$ et de rayon ${\displaystyle R}$ a pour équation ${\displaystyle (x-x_{0})^{2}+(y-y_{0})^{2}+(z-z_{0})^{2}+(w-w_{0})^{2}=R^{2}}$.

D'autres systèmes de coordonnées, comme les coordonnées hypersphériques, ou les coordonnées de Hopf, sont plus adaptés à l'étude des déplacements de l'espace à quatre dimensions, en particulier des rotations[32].

L'espace de Minkowski utilise le même système de coordonnées cartésiennes (en remplaçant ${\displaystyle w}$ par ${\displaystyle t}$, représentant le temps), mais remplace le produit scalaire précédent par un pseudo-produit scalaire défini par la formule ${\displaystyle \mathbf {a} \cdot \mathbf {b} =a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}-c^{2}a_{4}b_{4}}$ (où ${\displaystyle c}$ est la vitesse de la lumière) et associé à une forme quadratique de signature ${\displaystyle (+,+,+,-)}$ ; celle-ci modélise l'intervalle d'espace-temps. La géométrie de cet espace (si on interprète ce pseudo-produit scalaire comme un produit scalaire ordinaire) est non euclidienne, et possède même des propriétés incompatibles avec les définitions usuelles, la distance entre deux points pouvant être imaginaire, ou le cosinus d'un angle être supérieur à 1[n 16].

Plan de la maison biscornue, avant son repliement dans la quatrième dimension.

Les ouvrages de Hinton inspirèrent peut-être Edwin Abbott Abbott à publier Flatland en 1884, où il montre comment notre espace pourrait être perçu par un Carré, habitant d'un monde à deux dimensions, lequel finit par suggérer (sans grand succès) à la Sphère qui est venue le visiter qu'une quatrième dimension spatiale serait possible ; Hinton à son tour publia en 1906 un chapitre additionnel de Flatland[n 18]. Mais le plus souvent, la quatrième dimension est identifiée au temps, l'illustration la plus connue en étant La Machine à explorer le temps de H. G. Wells, dont une traduction est publiée au Mercure de France dès 1899[59].

En 1912, Gaston de Pawlowski est l’auteur d'un roman de science-fiction, Voyage au pays de la quatrième dimension[60], qui utilise véritablement une dimension spatiale supplémentaire ; de nombreux textes analogues suivront, par exemple la nouvelle de Robert Heinlein, La Maison biscornue, décrivant avec humour le repliement d'un patron de tesseract[61].

Plusieurs ouvrages de vulgarisation ont popularisé certaines de ces idées auprès du grand public, depuis les exposés de Poincaré dans La Science et l'Hypothèse jusqu'aux livres de Rudy Rucker[62] ; à partir des années 1990, les progrès de l'infographie ont permis des réalisations plus abordables encore, telles que le film Dimensions... une promenade mathématique[63].

Le Monument à la Constitution, à Madrid.

Les modèles d'objets à quatre dimensions (ou plus exactement de leurs projections dans notre espace) ont très tôt inspiré peintres et sculpteurs[64] ; Maurice Princet a même pu affirmer l'influence de certains croquis de Jouffret sur des œuvres cubistes telles que le portrait d'Ambroise Vollard par Picasso[65] - [66] ; plus explicitement, Salvador Dalí, dans Corpus hypercubus, a représenté une crucifixion sur un patron d'hypercube[67].

L'Arche de la Défense a été parfois vue comme une projection tridimensionnelle d'un tesseract[68] ; le monument à la Constitution de 1978, à Madrid, est plus délibérément construit à partir d'une telle projection. De nombreuses sculptures ont été également réalisées à partir de diverses représentations d'objets quadridimensionnels, combinant des objectifs esthétiques et pédagogiques[n 19].

L'idée d'une quatrième dimension habitée par des êtres supérieurs à nous ou des esprits (voire des fantômes) est assez fréquente dès le début du XX^e siècle dans des textes ésotériques, par exemple dans ceux de Piotr Ouspenski, ou encore dans un ensemble de conférences données par Rudolf Steiner en 1905[70], mélangeant des résultats mathématiques rigoureux à des interprétations mystiques, facilitées comme on l'a vu par la possibilité, en utilisant la quatrième dimension (si elle était physiquement accessible), d'opérer des miracles apparents. De même, les opérations de chirurgie psychique ont été décrites dans les années 1960 comme relevant d'une « chirurgie de la quatrième dimension »[71].

Certaines propriétés de l'espace à quatre dimensions, par exemple la transformation en image dans un miroir à la suite d'un simple déplacement, ont été exploitées par des auteurs de fantastique, comme le fait Lovecraft dans La Maison de la sorcière ; le mythe de Cthulhu contient d'ailleurs plusieurs autres références à des géométries incompréhensibles, comme la capacité des chiens de Tindalos à se déplacer en utilisant les angles du temps[72] - [73].

De nombreux films fantastiques et de science-fiction font référence à la quatrième dimension, le plus souvent en la confondant avec le temps ; plus géométriquement, Cube 2 et Interstellar utilisent un tesseract comme une sorte de labyrinthe permettant également un accès à d'autres époques, voire à des univers parallèles[74].

: document utilisé comme source pour la rédaction de cet article.

• Esprit Jouffret, Traité élémentaire de géométrie à quatre dimensions et introduction à la géométrie à n dimensions, Paris, Gauthier-Villars, 1904, 227 p. (ISBN 2-87647-221-X, lire en ligne).  .
• (en) R. C. Archibald, « Time as a Fourth Dimension » [« Le temps comme une quatrième dimension »], Bulletin of the American Mathematical Society,‎ 1914, p. 409-412 (lire en ligne).
• (en) Eward Hope Neville, The Fourth Dimension [« La quatrième dimension »], Cambridge University Press, 1921, 56 p. ([lire en ligne] sur le site d'histoire des mathématiques de l'université du Michigan).
• (en) Andrew Forsyth, Geometry of Four Dimensions [« Géométrie à quatre dimensions »], Cambridge University Press, 1930, 513 p. ([lire en ligne] sur Internet Archive).
• George Gamow (trad. de l'anglais par Junior et Maurice Gauzit), Un, deux, trois ... l'infini [« One, Two, Three... Infinity »], Paris, Dunod, 1955, 282 p. (OCLC 490990286) (chapitre 4 de la version originale : le monde à quatre dimensions (en)).
• (en) Harold Scott MacDonald Coxeter, Regular Polytopes [« Polytopes réguliers »], New York, Dover Publishing, 1973, 3^e éd., 321 p. (ISBN 978-0-486-61480-9, lire en ligne ). 
• Rudy Rucker (trad. de l'anglais), La quatrième dimension [« The Fourth Dimension: Toward a Geometry of Higher Reality »], Paris, Seuil, 1985, 352 p. (ISBN 978-2020477994).
• Michel Paty, Les trois dimensions de l'espace et les quatre dimensions de l'espace-temps, in Dimension, dimensions (ouvrage collectif sous la direction de Dominique Flament), Paris, Fondation Maison des Sciences de l’Homme, 1998 (lire en ligne), p. 97-112.

• Espace-temps
• Quatrième dimension (art)

• Quatre vidéos de Mickaël Launay sur la quatrième dimension : Définition, Représenter la 4D, Les curiosités de la 4D, L'hypercube.
• Site officiel du projet Dimensions, sur lequel on trouvera en particulier des liens vers tous les films, ainsi que des textes complémentaires.
• (en) Animations d'objets en 4D (projections et coupes)