Icositétrachore
L'icositétrachore, ou « 24-cellules » est un 4-polytope régulier convexe. Il est spécifique à la dimension 4 dans le sens où il ne possède aucun équivalent dans une autre dimension. On le dénomme aussi « 24-cellules », « icositétratope », ou « hypergranatoèdre ».
| Icositétrachore (24-cellules) | |
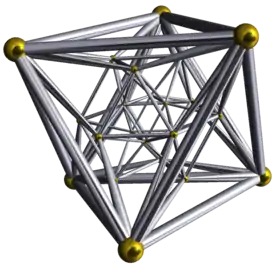 Diagramme de Schlegel (sommets et arêtes) | |
| Type | Polychore régulier |
|---|---|
| Cellules | 24 {3,4} |
| Faces | 96 {3} |
| Arêtes | 96 |
| Sommets | 24 |
| Symbole de Schläfli | {3,4,3} t1{3,3,4} t1{31,1,1} |
| Polygone de Pétrie | Dodécagone |
| Groupe(s) de Coxeter | F4, [3,4,3] o(1152) B4, [4,3,3] o(384) D4, [31,1,1] o(192) |
| Diagramme de Coxeter-Dynkin | |
| Dual | Lui-même |
| Propriétés | Convexe, isogonal, isotoxal, isoédral |
Sommets
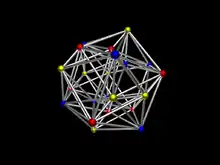
On peut définir un icositétrachore dans au moyen des sommets de coordonnées , ainsi que ceux obtenus en permutant ces coordonnées. Ils sont au nombre de 24.
On peut répartir ces sommets en trois familles dont chacune correspond aux sommets d'un hexadécachore :
- HexaDec[1] : et
- HexaDec[2] : et
- HexaDec[3] : et
Si on regroupe ensemble deux de ces hexadécachores, on obtient les sommets d'un tesseract. Par exemple, les sommets de Hexadec[1] et Hexadec[2] donnent le tesseract suivant :
- (1,1,0,0) (1,0,0,1) (1,0,0,–1) (1,–1,0,0) carré de côtés (0,–1,0,1) et (0,–1,0,–1)
- (0,1,1,0) (0,0,1,1) (0,0,1,–1) (0,–1,1,0) translaté du précédant de (–1,0,1,0) pour former un cube,
cube qu'on translate de (–1,0,–1,0) pour obtenir les derniers sommets :
- (0,1,–1,0) (0,0,–1,1) (0,0,–1,–1) (0,–1,–1,0)
- (–1,1,0,0) (–1,0,0,1) (–1,0,0,–1) (–1,–1,0,0)
Arêtes
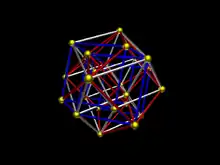
Les arêtes de l'icositétrachore sont ceux des trois tesseracts qu'on peut définir de la façon précédente. Dans l'exemple ci-dessus, ce sont aussi les segments joignant deux sommets distants de . Ils sont au nombre de 96. Chaque sommet appartient à huit arêtes.
Faces
Les faces sont des triangles équilatéraux, dont les sommets sont distants de . Dans l'exemple ci-dessus, les sommets d'une face ont pour coordonnées , , , ou bien , , (ainsi que ceux obtenus par une même permutation), avec , , et . Ils sont au nombre de 96. Chaque face possède un et un seul sommet de chaque hexadécachore défini plus haut.
Cellules
Les cellules sont des octaèdres réguliers. Dans l'exemple précédent, huit octaèdres sont contenus dans les hyperplans d'équation , , , , et seize autres sont contenus dans les hyperplans d'équation . Il y a 24 cellules en tout.
Dual
Le polytope dual de l'icositétrachore précédent possède pour sommets les points de coordonnées , ainsi que les points analogues obtenus par permutation des coordonnées, et les points de coordonnées . Il s'agit également d'un icositétrachore, de sorte que l'icositétrachore est autodual.
Lien externe
Icositétrachore sur MathCurve.
























