Statistique de Fermi-Dirac

En mécanique quantique et en physique statistique, la statistique de Fermi-Dirac désigne la distribution statistique de fermions indiscernables (tous similaires) sur les états d'énergie d'un système à l'équilibre thermodynamique. La distribution en question tient à une particularité des fermions : les particules de spin demi-entier sont assujetties au principe d'exclusion de Pauli, à savoir que deux particules ne peuvent occuper simultanément un même état quantique (voir l'article Gaz de Fermi).

Note historique

Avant l'avènement de la distribution de Fermi-Dirac dans les années 1920, la compréhension du comportement des électrons dans les métaux était très rudimentaire. Le modèle de Drude utilisait la statistique classique de Maxwell-Boltzmann pour décrire la dynamique des électrons. Ainsi les scientifiques ne comprenaient pas bien pourquoi les électrons participaient en grand nombre dans la conduction du courant électrique dans un métal et que ce nombre devenait extrêmement réduit quand il s'agit de contribuer à la capacité calorifique du même métal. Il y a manifestement ici un problème de statistique qui se pose dans l'évaluation de la capacité calorifique des métaux.

L'explication fut apportée par le modèle de l'électron libre de Arnold Sommerfeld (1927) qui introduisait la distribution de Fermi-Dirac, en révélant que seuls les états situés près du niveau de Fermi, étaient sollicités pour la contribution à la capacité calorifique du métal.

Distribution de Fermi–Dirac

La statistique de Fermi-Dirac a été introduite en 1926 par Enrico Fermi et Paul Dirac. En 1927 elle fut appliquée aux électrons dans un métal par Arnold Sommerfeld. Statistiquement, le nombre n_i de particules dans l'état d'énergie E_i est donné par :

n_{i}={\frac {g_{i}}{\exp \left({\frac {E_{i}-\mu }{k_{\rm {B}}T}}\right)+1}}\

où :

g_i est la dégénérescence de l'état d'énergie E_i , à savoir le nombre d'états possédant cette énergie ;
μ est le potentiel chimique ;
k_B est la constante de Boltzmann ;
T est la température absolue.

Utilisation

Les distributions de Fermi-Dirac pour les fermions, en même temps que la distribution de Bose-Einstein analogue pour les bosons, sont utilisées lorsque les effets quantiques sont pris en compte, et lorsque les particules sont considérées comme indiscernables. Cela correspond à une concentration de particules (N/V) supérieure à une certaine densité d'état, c'est-à-dire que la distance intermoléculaire est inférieure à celle de la longueur d'onde thermique de de Broglie.

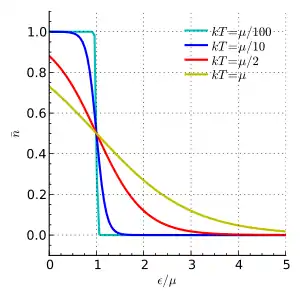Distribution de Fermi-Dirac en fonction de ε/μ et de différentes températures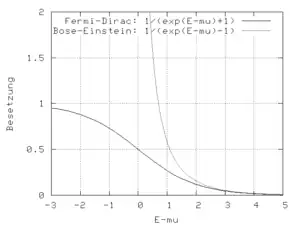
$Représentation de ⟨ n ( E ) ⟩ {\displaystyle \langle n(E)\rangle } pour les bosons (courbe du haut) et les fermions (courbe du bas).$
Représentation de $\langle n(E)\rangle$ pour les bosons (courbe du haut) et les fermions (courbe du bas).

Entropie et dérivation dans l'ensemble microcanonique

L'entropie d'un système constitué par des fermions, décrits par des fonctions d'onde antisymétriques (spin demi-entier), peut être trouvée en utilisant le principe d'exclusion de Pauli et la description statistique due à J. Willard Gibbs[1]. Elle vaut

S=-k_{\rm {B}}\sum _{j}G_{j}\left[(1-n_{j})\log {(1-n_{j})}+n_{j}\log n_{j}\right]

où

$k_{\rm {B}}$	constante de Boltzmann,
$n_{j}$	nombre d'occupation (proportion de fermions dans un état d'énergie donné),
$G_{j}$	nombre d'états possibles dans le groupe j (dégénérescence).

Démonstration

En suivant la méthode énoncée par J.W. Gibbs en physique statistique et le principe d'exclusion de Pauli, on dénombre dans le système étudié les fermions d'énergie E_j, leur nombre dans ce groupe N_j, chacun de ces groupes pouvant comporter G_j états. Le calcul de l'entropie revient à calculer le poids statistique Ω d'un tel système, c'est-à-dire le nombre de micro-états accessibles permettant de réaliser cet état macroscopique. Chaque groupe étant supposé indépendant on a Ω = Π_j Ω_j. Le problème est donc ramené à la connaissance de Ω_j.

Le nombre de possibilités de répartir N_j fermions identiques dans G_j états avec au plus une particule par état (selon le principe de Pauli) est

\Omega _{j}={\frac {G_{j}!}{N_{j}!(G_{j}-N_{j})!}}

En utilisant la formule de Stirling $\log {N!}\approx N\log {N}$ on calcule l'entropie

S=k_{\rm {B}}\log \Omega =k_{\rm {B}}\sum _{j}\log \Omega _{j}=k_{\rm {B}}\sum _{j}\left[G_{j}\log {G_{j}}-N_{j}\log {N_{j}}-(G_{j}-N_{j})\log {(G_{j}-N_{j})}\right]

Soit, en introduisant le nombre d'occupation $n_{j}={\frac {N_{j}}{G_{j}}}$

S=-k_{\rm {B}}\sum _{j}G_{j}\left[n_{j}\log n_{j}+(1-n_{j})\log {(1-n_{j})}\right]

Dans l'ensemble microcanonique, les variables thermodynamiques à l’équilibre sont obtenus par maximisation de l'entropie sous contrainte de respecter le nombre total de fermions $N=\sum _{i}G_{i}n_{i}$ et l'énergie totale $E=\sum _{i}n_{i}G_{i}E_{i}$ . En utilisant la méthode des multiplicateurs de Lagrange, α pour le nombre de particules et β pour l'énergie, la solution vérifie

{\frac {\partial }{\partial n_{j}}}\left(S-\alpha N-\beta E\right)=0\,,\qquad \forall j

La solution de ce système d'équations indépendantes est la distribution statistique de Fermi-Dirac

n_{j}={\frac {1}{\mathrm {e} ^{\alpha +\beta E_{j}}+1}}

On peut retrouver les valeurs de α et β à partir du premier principe de la thermodynamique. Donc, α=-μ β et β=(k_BT)^-1.

Limite classique et comparaison avec les bosons

Comparaison des distributions de Fermi-Dirac, Bose-Einstein et Maxwell-Boltzmann.

À haute température, lorsque les effets quantiques ne se font plus sentir, la statistique de Fermi-Dirac tend vers la statistique de Maxwell-Boltzmann ; il en est de même pour la statistique de Bose-Einstein qui régit les bosons. À basse température, si les particules occupent en priorité les niveaux d'énergie les plus faibles, les statistiques diffèrent cependant. Par exemple, à température nulle :

avec la statistique de Fermi-Dirac, le niveau de plus basse énergie, E₀, est occupé par au plus g₀ fermions ; les états de basse énergie E_i sont ensuite occupés chacun dans l'ordre croissant des énergies par au plus g_i fermions jusqu'à épuisement de ces derniers;
avec la statistique de Bose-Einstein, le niveau de plus basse énergie contient tous les bosons (cas limite du condensat de Bose-Einstein).

Ensembles de fermions

Les électrons dans les solides forment un gaz de fermions dont la description requiert la statistique de Fermi-Dirac. Récemment, le refroidissement de gaz d'atomes dilués fermioniques jusqu'à des températures de l'ordre du μK a permis d'obtenir des condensats fermioniques, uniquement descriptibles par cette statistique.

Notes et références

Cet article est partiellement ou en totalité issu de l'article intitulé « Entropie (fermions) » (voir la liste des auteurs).

(en) Lev Landau et Evgueni Lifchits, Statistical Physics, Pergamon Press, 1969 (lire en ligne)

Voir aussi

Bibliographie

Charles Kittel (trad. Nathalie Bardou, Évelyne Kolb), Physique de l’état solide [« Solid state physics »], 1998 [détail des éditions]
(en) Lev Landau et Evgueni Lifchits, Statistical Physics, Pergamon Press, 1969 (lire en ligne)