Gaz de Fermi
Un gaz de Fermi idéal est un état de la matière constitué d'un ensemble de nombreux fermions sans interaction. Les fermions sont des particules ayant un spin demi-entier (1/2, 3/2), comme les électrons, les protons et les neutrons ; la propriété essentielle des fermions est de ne pas pouvoir occuper en même temps le même état quantique, en raison du principe d'exclusion de Pauli.
Les fermions obéissent donc aux lois de la statistique de Fermi-Dirac, loi qui détermine la distribution d'énergie des fermions dans un gaz de Fermi en équilibre thermique et caractérise leur densité numérique, leur température et l'ensemble des états d'énergie disponibles.

Le modèle du gaz de Fermi (d'après le nom du physicien italien Enrico Fermi[1]), bien que basé sur les principes de la mécanique quantique, a des applications dans tous les domaines de la physique : de l'infiniment petit (noyau de l'atome) à la cosmologie (dynamique stellaire) en passant par la physique du solide.
Dans sa formulation de base, il décrit un système uniforme de fermions : aux propriétés identiques dans tout l'espace, sans interaction, à température nulle. Apparemment très restrictives, ces hypothèses sont une très bonne approximation pour de nombreux systèmes dont la température thermodynamique n'est pas nulle (voir infra)[2].
Les extensions du modèle tendent à s'affranchir de ces contraintes (voir infra) : température finie traitée à l'aide de la statistique de Fermi-Dirac ; systèmes non-uniformes dans l'espace, avec par exemple, l'approximation de Thomas-Fermi ; effets relativistes dans l'expression de l'énergie, etc.
Cet article est consacré d'abord à la présentation du calcul des grandeurs fondamentales d'un gaz de Fermi, à température nulle : dans le cas modèle à 1 dimension, puis dans le cas plus réaliste à 3 dimensions ; lorsque le nombre de particules est limité, on peut effectuer un calcul discret ; lorsque le nombre de particules est très grand, on peut le traiter comme une variable continue.
Description générale
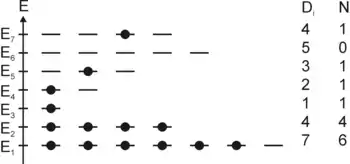
Gaz de fermions vs. gaz de bosons
Un gaz de Fermi idéal (ou gaz de Fermi libre) est un modèle physique pour un ensemble de fermions sans interaction, dans un puits de potentiel constant, et donc homogène. Les fermions sont des particules élémentaires ou composites de spin demi-entier, qui suivent donc les lois de la statistique de Fermi-Dirac. Le modèle équivalent pour les particules ayant un spin entier (gaz de Bose pour un ensemble de bosons sans interaction) s'appuie sur la statistique de Bose-Einstein. Lorsque la densité numérique de particules est suffisamment faible et la température élevée, le gaz de Fermi et le gaz de Bose se comportent comme un gaz parfait classique (voir infra)[2].
En application du principe d'exclusion de Pauli, aucun état quantique caractérisé par un ensemble de nombres quantiques ne peut être occupé par plus d'un fermion. Ainsi, dans un gaz de Fermi libre (sans interaction), contrairement à un gaz de Bose, seul un petit nombre de particules peuvent occuper un domaine d'énergie donné ; donc un gaz de Fermi libre ne peut se condenser en un condensat de Bose-Einstein, où toutes les particules occupent le même état quantique. Pour qu'un gaz de Fermi puissent se condenser, il est nécessaire que les particules interagissent pour former des paires de Cooper (paires de fermions couplés de spin total 0), qui suivent la statistique de Bose-Einstein et peuvent former un condensat (voir par exemple la théorie BCS de la supraconductivité)[3].
Caractéristiques du gaz de fermions
L'énergie totale du gaz de Fermi au zéro absolu est supérieure à la somme des états fondamentaux à une seule particule, car le principe de Pauli agit comme une sorte d'interaction ou de pression (pression de dégénérescence) qui maintient les fermions dans des états excités, séparés et en mouvement. Cette énergie maximale des fermions à température nulle est appelée énergie de Fermi (voir infra). Pour la même raison, la pression d'un gaz de Fermi ne peut jamais s'annuler, même à température nulle, contrairement à celle d'un gaz parfait classique. On associe à l'énergie de Fermi une température (température de Fermi), en dessous de laquelle le gaz peut être considéré comme dégénéré (sa pression dérive presque exclusivement du principe de Pauli). Cette température dépend de la masse des fermions et de la densité des états d'énergie (voir infra).
Pour certains systèmes, la température de Fermi est beaucoup plus élevée que leur température thermodynamique ; dans ce cas, la théorie du gaz à température est utilisable avec un bon niveau d'approximation. C'est la cas, par exemple des étoiles à neutrons[4] (gaz de Fermi de neutrons) ou ou des naines blanches (un gaz de Fermi d'électrons)[5].
Le modèle du gaz de Fermi idéal à température nulle s'applique aussi dans l'étude de la conduction des charges électriques dans un métal cristallin[6] ; car, d'une part, l'hypothèse principale (modèle d'électrons libres) est que leurs interactions réciproques sont négligeables en raison de l'effet d'écran ; et que d'autre part, la température de Fermi est généralement de plusieurs milliers de Kelvin, bien au-dessus de la température du laboratoire.
Une extension du modèle à l'étude de la structure cristalline des métaux et des semi-conducteurs, s'appuie sur le modèle d'électrons quasi libres dans lequel les électrons dans un réseau cristallin sont remplacés par un vecteur d'onde avec une impulsion cristalline correspondante[7] (cf. la théorie des bandes). Le modèle constitue le point de départ de théories plus avancées qui traitent des interactions, par exemple en utilisant la théorie des perturbations.
Propriétés d'un gaz uniforme à 1 dimension
On suppose que le gaz de fermions est contenu dans un puits carré infini de longueur L ; l'énergie potentielle d'une particule est donc :
C'est un modèle standard en mécanique quantique pour lequel la solution de l'équation de Schrödinger est bien connue[8]. Étant donné que le potentiel à l'intérieur de la boîte est uniforme, ce modèle est aussi appelé gaz uniforme 1D, même si le profil de densité numérique réel du gaz peut être non-uniforme, lorsque le nombre total de particules est petit.
Les niveaux sont labellisés par un seul nombre quantique n - strictement positif- et les énergies sont analytiquement calculables :
où est l'énergie du niveau de référence (qui peut être choisie arbitrairement), la masse d'un fermion, et est la constante de Planck réduite.
Pour les fermions (de spin ), les deux orientations possibles de spin ( ou ) définissent deux états quantiques de même énergie ; selon le principe de Pauli, deux particules au plus pourront donc occuper le même niveau d'énergie (dégénérescence d'ordre 2). Dans la configuration pour laquelle l'énergie totale est la plus faible (l'état fondamental), tous les niveaux d'énergie jusqu'à n = N /2 sont occupés et tous les niveaux supérieurs sont vides.
Par rapport à l'énergie de référence , l'énergie de Fermi est donc donnée par :
où est la partie entière de la fraction N /2.
Limite thermodynamique
Dans la limite thermodynamique, le nombre total de particules N est si grand que le nombre quantique n peut être traité comme une variable continue. Dans ce cas, la densité numérique de particules dans la boîte peut être considérée comme uniforme.
Une caractéristique essentielle est la densité des états par unité de volume, en fonction de l'énergie :
est le volume dans ce cas (1D) ; c'est une fonction décroissante de l'énergie, ce qui est spécifique au puits carré, d'autres formes de puits de potentiel (puits parabolique, potentiel coulombien dans les atomes) conduisent à des densités d'états croissantes avec l'énergie[9].
On part du nombre d'états quantiques dans l'intervalle , qui tient compte de la dégénérescence des fermions de spin 1/2 :
En supposant que l''énergie de référence est choisie comme nulle, en traitant comme une variable continue :
Le taux de dégénérescence des états électroniques en fonction de l'énergie est donc :
Et la densité d'états en fonction de l'énergie vaut :
Dans la littérature[10], est parfois aussi appelée la "densité d'états", diffère alors de par un facteur de volume du système.
Dans la limite de la température thermodynamique nulle, le taux d'occupation des niveaux d'énergie est une fonction de Heaviside :
tous les niveaux au-dessus de l'énergie de Fermi sont inoccupés ; cette dernière est déterminée par la contrainte qu'il y a N fermions dans les états occupés : , d'où l'expression de l'énergie de Fermi ::
On retrouve l'expression précédente à la limite des grands nombres .
Propriétés d'un gaz uniforme en 3 dimensions
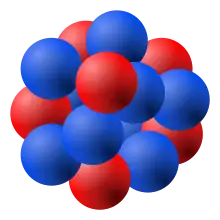
Le cas du gaz de Fermi uniforme, isotrope et non relativiste à 3 dimensions, est connu sous le nom de « sphère de Fermi ».
Les particules sont confinées dans un puits carré infini tridimensionnel, (c'est-à-dire une boîte cubique d'arête L) ; l'énergie potentielle est donc :
Les états quantiques sont maintenant labellisés par trois nombres quantiques et , entiers strictement positifs. Les énergies des particules individuelles sont [8]:
Dans ce cas, plusieurs états ont la même énergie (niveaux d'énergie dégénérés). Posant la constante et , et tenant compte du spin, les énergies et les dégénérescences des premiers niveaux sont :
Les niveaux d'énergie ne sont plus régulièrement espacés et leur dégénérescence est très variable.
Limite thermodynamique
Comme dans le cas du puits à une dimension, on peut considérer le cas où N est si grand que les nombres quantiques et peuvent être traités comme des variables continues.
Energie de Fermi
Chaque état quantique peut être défini dans un espace à 3 dimensions par le vecteur , avec l'énergie
est le carré de la longueur euclidienne, .
Le nombre d'états d'énergie inférieure à est égal au nombre d'états qui se trouvent dans une sphère de rayon , dans la région de l'espace où sont positifs. Dans l'état fondamental, ce nombre est égal au nombre de fermions dans le système :.
Le facteur deux prend en compte les deux états de spin et le facteur 1/8 tient compte du fait que le calcul est limité à la fraction de la sphère qui se trouve dans la région où tous les n sont positifs :
L'énergie de Fermi (par rapport à l'énergie de référence ) est alors exprimée comme:
Cette équation relie l'énergie de Fermi et le nombre de particules par unité de volume (lorsque l'on fait apparaître le volume remplacé par ) :
L'énergie totale d'une sphère de Fermi de fermions (qui occupent tous les états d'énergie dans la sphère de Fermi) est donnée par :. .
Par conséquent, l'énergie moyenne par particule est donnée par :
Densité des états

Pour un gaz de Fermi uniforme 3D, d'énergie de Fermi , la densité d'états s'obtient à partir da la variation du nombre de particules en fonction de l'énergie :
d'où la densité d'états (nombre d'états d'énergie par énergie, par unité de volume) qui s'obtient par la dérivée du nombre de particules par rapport à l'énergie :
La densité d'états augmente avec l'énergie. Par intégration directe sur le nombre de particules à une énergie donnée :
on retrouve l'expression de l'énergie interne du gaz de fermions :
Pression de dégénérescence
En utilisant la première loi de la thermodynamique, l'énergie (interne) permet l'expression de la pression, c'est-à-dire
cette expression, connue sous le nom de « pression de dégénérescence », reste valable pour des températures non nulles, mais inférieures à la température de Fermi. En ce sens, les systèmes composés de fermions constituent une matière dégénérée.
À la fin de la vie d'une étoile standard, lorsque les processus thermiques s'affaiblissent, elles peuvent devenir une naine blanche en s'effondrant sur elle-même, processus qui se stabilise lorsque la gravité est compensée par la pression de dégénérescence des électrons. En utilisant le gaz de Fermi comme modèle, il est possible de calculer la masse limite de Chandrasekhar, c'est-à-dire la masse maximale que toute étoile peut acquérir (sans pression significative générée thermiquement) avant de s'effondrer dans un trou noir ou une étoile à neutrons.
Une étoile à neutrons est une étoile principalement composée de neutrons, dont l'effondrement est également évité par la pression de dégénérescence de ces derniers.
Dans le cas des métaux, la pression de dégénérescence des électrons contribue à la compressibilité (son module d'élasticité isostatique) du matériau.
Exemples typiques de gaz de Fermi
Ce modèle physique peut être appliqué à la description précise de nombreux systèmes avec de nombreux fermions.
Les métaux
Selon le modèle de l'électron libre, les électrons d'un métal peuvent être considérés comme formant un gaz de Fermi uniforme. La densité numérique d'électrons de conduction dans les métaux varie entre environ 10 28 et 10 29 électrons par m3, ce qui est aussi la densité typique des atomes dans la matière solide ordinaire. Cette densité numérique produit une énergie de Fermi de l'ordre :
où est la masse au repos de l'électron[11]. Cette énergie de Fermi correspond à une température de Fermi de l'ordre de 10 6 K, bien supérieure à la température de la surface du Soleil. Tout métal s'évaporerait bien avant d'atteindre cette température sous la pression atmosphérique. Ainsi, dans les applications pratiques, les électrons de conduction dans un métal peuvent être considérés, en première approximation, comme constituant un gaz de Fermi à température nulle, car sa température est très petite devant la température de Fermi.
Naines blanches
Les naines blanches sont des étoiles dont la masse est comparable à celle du Soleil, mais leur rayon est environ cent fois plus petit que celui du Soleil (elles sont donc environ un million de fois plus denses que lui).
Ces densités élevées impliquent que les électrons ne sont plus liés à des noyaux uniques et forment un gaz d'électrons dégénéré. La densité numérique des électrons dans une naine blanche est de l'ordre de 10 36 électrons/m3 ; cela signifie que leur énergie de Fermi est :
ce qui correspond à des températures de l'ordre de K à comparer à la température maximale observée de K (voir l'article Naine blanche).
Noyau atomique
Un autre exemple typique est celui des particules dans un noyau d'atome. Le rayon du noyau vaut approximativement : ,
où A est le nombre de nucléons.La densité numérique des nucléons dans un noyau se déduit donc :
Cette densité doit être (approximativement) divisée par deux, car les protons et les neutrons constituent deux gaz de Fermi distincts. La présence de neutrons n'affecte pas l'énergie de Fermi des protons dans le noyau, et vice versa.
L'énergie de Fermi d'un noyau vaut environ :
où est la masse du proton.
Les noyaux sont à bords diffus et l'approximation de son potentiel par un puits carré est une première approximation ; la valeur typique de l'énergie de Fermi nucléaire est généralement estimée à 37 MeV[12].
Gaz de Fermi dans un potentiel harmonique
Parmi les extensions du modèle au cas des fermions contenus dans un potentiel plus général, le cas du potentiel harmonique à 3 dimensions a de nombreuses applications en physique moderne ; le potentiel s'écrit :
La densité d'états est[13] :
où est la fréquence propre de l'oscillateur ; et donc l'énergie de Fermi pour des particules d'un spin donné est :
Grandeurs physiques associées
L'énergie de Fermi et la densité de niveaux sont les paramètres de base pour caractériser les gaz de Fermi. D'autres grandeurs physiques leur sont associées.
La température de Fermi est définie par , où est la constante de Boltzmann ; lorsque la température thermodynamique du système est comparable , les effets thermiques sont comparables aux effets quantiques associés à la statistique de Fermi[14]. La température de Fermi pour un métal est de quelques ordres de grandeur au-dessus de la température ambiante (voir supra).
D'autres grandeurs sont utilisées : le moment de Fermi et la vitesse de Fermi , qui sont respectivement la quantité de mouvement et la vitesse de groupe d'un fermion à la surface de Fermi. La quantité de mouvement de Fermi peut également s'écrire comme , où est le rayon de la sphère de Fermi aussi appelé vecteur d'onde de Fermi [15].
Ces expressions sont bien définies seulement dans les cas où la surface de Fermi est à symétrie sphérique.
Traitement à température finie
Potentiel chimique à température non nulle
Pour un gaz de fermions à une température non nulle, la grandeur pertinente pour l'occupation des niveaux d'énergie est le potentiel chimique total μ (niveau de Fermi). En supposant que la concentration de fermions ne change pas avec la température, le potentiel chimique du gaz de Fermi idéal tridimensionnel est lié à l'énergie de Fermi à température nulle par un développement de Sommerfeld (avec ) :
où est la température [16].
Par conséquent, le potentiel chimique, , est approximativement égal à l'énergie de Fermi à des températures bien inférieures à la température de Fermi caractéristique . Cette température caractéristique est de l'ordre de 10 5 K pour un métal, donc à température ambiante (300 K), l'énergie de Fermi et le potentiel chimique interne sont sensiblement équivalents.
Grand ensemble canonique
La plupart propriétés calculées ci-dessus sont exactes à température nulle, mais restent de bonnes approximations pour des températures inférieures à la température de Fermi. Pour les autres grandeurs thermodynamiques, il faut s'appuyer sur un potentiel thermodynamique.
Pour un ensemble de fermions identiques, à température, volume et potentiel chimique µ fixes, on doit partir de l'ensemble grand canonique, dont la (grande) fonction de partition pour les fermions s'écrit[17]:
où , indexe les ensembles de tous les micro-états possibles qui donnent la même énergie totale ; est le nombre total de particules qui se déduit du taux d'occupation ; est l'énergie d'une seule particule dans l'état (avec un facteur 2 si l'énergie de l'état est dégénérée). D'où l'expression du grand potentiel :
- Comme vu précédemment, dans la limite macroscopique des grands nombres, il est possible d'utiliser une approximation continue (approximation de Thomas-Fermi) pour convertir cette somme discrète en une intégrale :
où D(ε) est la densité d'états en fonction de l'énergie.
Le grand potentiel est lié au nombre de particules à température finie :
:
où la dérivée est prise à température et volume fixes, ce qui fait apparaître la fonction de la distribution de Fermi-Dirac :.
De même, l'énergie interne totale est définie par :
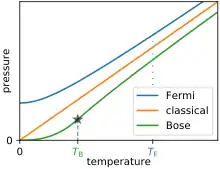
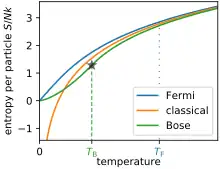
La figure ci-contre montre la comparaison entre l'entropie d'un gaz de Fermi, d'un gaz de Bose et d'un gaz classique en fonction de la température.
Extensions du modèle
Gaz de fermions en interaction
Lorsque l'on prend en compte l'interaction entre les fermions, le système de fermions n'est pas homogène dans l'espace ; les différentes quantités caractéristiques deviennent locales et dépendent de la position .
Le modèle de Thomas-Fermi est un modèle semi-classique développé initialement pour étudier la distribution des électrons autour de l'atome, soumis à leurs interactions mutuelles et à l'attraction du noyau. La grandeur de base est la densité volumique locale de particules , qui est liée au moment de Fermi local :
La densité d'énergie cinétique locale est alors proportionnelle à .
Gaz de Fermi relativiste
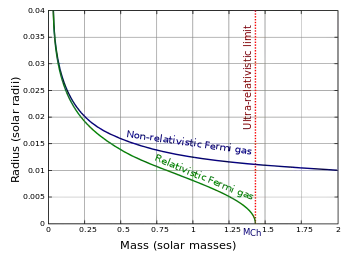
L'étude jusqu'à présent s'est limitée au cas non-relativiste où l'énergie est liée au carré de la quantité de mouvement. Dans le cadre plus général de la relativité restreinte, l'expression relativiste de l'énergie d'une particule est : où est la masse au repos de la particule. Pour un tel système, l'énergie de Fermi s'écrit :
Le modèle de gaz de Fermi relativiste est utilisé pour la description des grandes naines blanches proches de la limite de Chandrasekhar.
A la limite ultrarelativiste, l'énergie de masse au repos devient négligeable[16] :et le moment de Fermi s'écrit :
:
On en déduit que la pression de dégénérescence est proportionnelle à la puissance 4/3 de la densité de particules .
Liquide de Fermi
En 1956, Lev Landau développe la théorie du liquide de Fermi, où il traite le cas d'un système avec des interactions répulsives, pas nécessairement faibles, entre fermions. La théorie montre que les propriétés thermodynamiques d'un gaz de Fermi idéal et d'un liquide de Fermi ne diffèrent pas de manière essentielle.
On peut montrer que le liquide de Fermi est équivalent à un gaz de Fermi composé d'excitations collectives ou quasiparticules[18], chacune ayant une masse effective et un moment magnétique différents de ceux de la particule réelle.
Voir également
Notes et références
Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé Fermi gas (voir la liste des auteurs).
- (de) Fermi, « Zur Quantelung des idealen einatomigen Gases », Zeitschrift für Physik, vol. 36, nos 11–12, , p. 902–912 (ISSN 0044-3328, DOI 10.1007/BF01400221, Bibcode 1926ZPhy...36..902F, S2CID 123334672, lire en ligne [archive du ])
- Lev Davidovič Landau, Evgenij Mihailovič Lifšic et Sergeï Medvedev, Physique statistique, Éd. Mir Ellipses, coll. « Physique théorique », (ISBN 978-2-7298-9463-4, lire en ligne)
- Regal, Greiner et Jin, « Observation of Resonance Condensation of Fermionic Atom Pairs », Physical Review Letters, vol. 92, no 4, , p. 040403 (PMID 14995356, DOI 10.1103/PhysRevLett.92.040403, Bibcode 2004PhRvL..92d0403R, arXiv cond-mat/0401554, S2CID 10799388)
- (en) David Boal, « Fermi gas and neutron stars » [PDF], (consulté le )
- Ting-Hang Pei, « The Highly Accurate Relation Between the Radius and Mass of the White Dwarf Star From Zero to Finite Temperature », Frontiers in Astronomy and Space Sciences, vol. 8, (ISSN 2296-987X, DOI 10.3389/fspas.2021.799210, lire en ligne, consulté le )
- « Le gaz d électrons libres de Fermi » [html] (consulté le )
- Barreteau, « Les électrons dans les solides » [PDF], sur IRAMIS-CEA (consulté le )
- Christian Ngô et Hélène Ngô, Physique quantique: introduction avec exercices, Masson, coll. « Enseignement de la physique », (ISBN 978-2-225-82582-8)
- D. A. Butts et D. S. Rokhsar, « Trapped Fermi gases », Physical Review A, vol. 55, no 6, , p. 4346–4350 (DOI 10.1103/PhysRevA.55.4346, lire en ligne, consulté le )
- Giorgini, Pitaevskii et Stringari, « Theory of ultracold atomic Fermi gases », Reviews of Modern Physics, vol. 80, no 4, , p. 1215–1274 (DOI 10.1103/RevModPhys.80.1215, Bibcode 2008RvMP...80.1215G, arXiv 0706.3360, S2CID 117755089, lire en ligne)
- (en) Nave, « Fermi Energies, Fermi Temperatures, and Fermi Velocities », sur hyperphysics.phy-astr.gsu.edu, HyperPhysics (consulté le )
- Luc Valentin, Le monde subatomique: des quarks aux centrales nucléaires, Hermann, (ISBN 978-2-7056-6043-7)
- X X Yi et J C Su, « Fermi Gas in Harmonic Oscillator Potentials », Physica Scripta, vol. 60, no 2, , p. 117–119 (ISSN 0031-8949 et 1402-4896, DOI 10.1238/Physica.Regular.060a00117, lire en ligne, consulté le )
- Torre, « PHYS 3700: Introduction to Quantum Statistical Thermodynamics », Utah State University, (consulté le )
- Neil W. Ashcroft et N. David Mermin, Solid State Physics, Holt, Rinehart and Winston, (ISBN 978-0-03-083993-1, lire en ligne
 )
) - (en) Walter Greiner, Ludwig Neise et Horst Stöcker, Thermodynamics and Statistical Mechanics, New-York, Springer, coll. « Classical Theoretical Physics », , 463 p. (ISBN 0-387-94299-8, DOI 10.1007/978-1-4612-0827-3_14)
- Hélène Ngô et Christian Ngô, Physique statistique: introduction avec exercices, Masson, coll. « Enseignement de la physique », (ISBN 978-2-225-81287-3)
- David Pines et Philippe Nozières, The theory of quantum liquids. 1: Normal fermi liquids, Addison-Wesley, (ISBN 978-0-201-40774-7 et 978-0-201-09429-9)
Lectures complémentaires
- Neil W. Ashcroft et N. David Mermin, Solid State Physics (Harcourt : Orlando, 1976).
- Charles Kittel, Introduction à la physique du solide, 1ère éd. 1953 - 8e éd. 2005, (ISBN 0-471-41526-X)




























































![{\displaystyle N(E)={\frac {V}{3\pi ^{2}}}\left[{\frac {2m}{\hbar ^{2}}}(E-E_{0})\right]^{3/2};\,0\leq (E-E_{0})\leq E_{F}\;,}](https://img.franco.wiki/i/a04b1ce4acc66272256c20f019001033d879a2ee.svg)
















![{\displaystyle \omega _{=}{\sqrt[{3}]{\omega _{x}\omega _{y}\omega _{z}}}}](https://img.franco.wiki/i/a58d06e5e547f85bd189ec3aa9213a2abe53d395.svg)









![{\displaystyle \mu (T)=E_{0}+E_{\mathrm {F} }\left[1-{\frac {\pi ^{2}}{12}}\left({\frac {k_{\rm {B}}T}{E_{\mathrm {F} }}}\right)^{2}-{\frac {\pi ^{4}}{80}}\left({\frac {k_{\rm {B}}T}{E_{\mathrm {F} }}}\right)^{4}+\cdots \right],}](https://img.franco.wiki/i/5b86297986bb976c0bf00030827a053380f5ca43.svg)



























