Intégrale curviligne

Intégrale curviligne d'un champ scalaire.

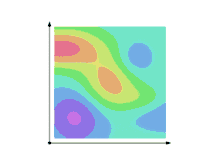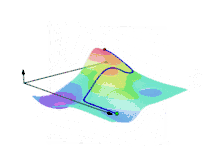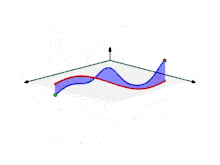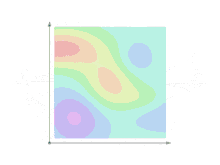
On définit l'intégrale curviligne d'un champ scalaire continu ${\displaystyle f:\Gamma \to \mathbb {R} }$ comme l'intégrale de Stieltjes de f∘γ par rapport à l'abscisse curviligne s_γ(t) (longueur de l'arc γ restreint à [a, t])[1] :

${\displaystyle \int _{\Gamma }f\ \mathrm {d} s=\int _{a}^{b}(f\circ \gamma )\,\mathrm {d} s_{\gamma },}$

c'est-à-dire la limite, quand le pas de la subdivision pointée de [a, b] tend vers 0, des sommes de Riemann associées :${\displaystyle \sum _{k=1}^{n}f(\gamma (t'_{k}))\left(s_{\gamma }(t_{k})-s_{\gamma }(t_{k-1})\right)}$ où la subdivision pointée est notée : a = t₀ < t₁ < … < t_n = b, t'_k ∈ [t_k–1, t_k].

Cette définition ne dépend pas du paramétrage de Γ, ni de l'orientation.

La longueur s_γ(b) de l'arc Γ est l'intégrale curviligne de la fonction constante 1.

Si γ est de classe C¹, ${\displaystyle \int _{\Gamma }f\ \mathrm {d} s=\int _{a}^{b}f(\gamma (t))\|\gamma '(t)\|\mathrm {d} t.}$

Circulation d'un champ vectoriel.

On définit également la circulation le long de Γ d'un champ vectoriel continu ${\displaystyle f:\Gamma \to \mathbb {R} ^{n}}$ comme une intégrale de Stieltjes :

${\displaystyle \int _{\Gamma }f\cdot \,\mathrm {d} \gamma =\int _{a}^{b}(f\circ \gamma )\cdot \,\mathrm {d} \gamma ,}$

où ∙ désigne le produit scalaire[2].

Cette définition ne dépend pas du paramétrage de Γ mais dépend de l'orientation (l'intégrale est changée en son opposée quand la courbe est parcourue en sens inverse).

On peut reformuler cette définition en notant ω la 1-forme différentielle « produit scalaire par f » : si ω est une 1-forme différentielle continue sur le support de Γ, on définit l'intégrale curviligne de ω le long de Γ par :

${\displaystyle \int _{\Gamma }\omega =\int _{a}^{b}\langle \omega \circ \gamma ,\mathrm {d} \gamma \rangle ,}$

où ⟨∙, ∙⟩ est le crochet de dualité.

Si γ est de classe C¹,${\displaystyle \int _{\Gamma }f\cdot \,\mathrm {d} \gamma =\int _{a}^{b}f(\gamma (t))\cdot \gamma '(t)\,\mathrm {d} t\quad {\rm {et}}\quad \int _{\Gamma }\omega =\int _{a}^{b}\omega _{\gamma (t)}(\gamma '(t))\,\mathrm {d} t.}$

Pour n = 2 et en identifiant ℝ² au plan complexe, on définit l'intégrale curviligne d'une fonction continue ${\displaystyle f:\Gamma \to \mathbb {C} }$ comme l'intégrale de la 1-forme différentielle « produit (complexe) par f » :

${\displaystyle \int _{\Gamma }f(z)\,\mathrm {d} z=\int _{a}^{b}(f\circ \gamma )\,\mathrm {d} \gamma .}$

Si γ est de classe C¹, ${\displaystyle \int _{\Gamma }f(z)\,\mathrm {d} z=\int _{a}^{b}f(\gamma (t))\gamma '(t)\,\mathrm {d} t.}$

Lorsque Γ est une courbe fermée (ses deux extrémités coïncident), il arrive qu'on utilise la notation : ${\displaystyle \oint _{\Gamma }f(z)\,\mathrm {d} z.}$

• Théorème de Stokes
• Intégrale de surface
• Méthodes de calcul d'intégrales de contour